声学隐身层结构对隐身性能的影响

2020-03-23马建敏

声学技术 2020年1期

尹可，马建敏

(复旦大学航空航天系，上海200433)

0 引言

声学隐身是在电磁隐身的基础上提出的新概念。21 世纪初，Pendry J B 等[1]和Leonhardt U[2]基于变换电磁波理论和电磁超材料技术提出了电磁波隐身理论。Cummer S A 等[3]基于声波方程和麦克斯韦(Maxwell)方程的形式相似性，将变换理论和超材料技术应用于二维声场，开启了对声隐身的探索。随后，Chen H Y 等[4]将声学隐身扩展到三维空间，扩大了声学隐身的应用范围。声学隐身技术可以通过控制声波绕射来减弱声波的散射，引起了人们广泛的关注和极大的兴趣，大量学者围绕隐身层的隐身机理和结构设计等方面展开了研究，已经取得有价值的成果，开辟了许多新的研究方向和领域[5-11]。

由变换声学理论计算得到的理想声学隐身层的物性参数(密度和体弹性模量)是各向异性、连续变化和奇异的，在工程上很难实现。Huang Y 等[12]提出利用由两种不同的均匀各向同性材料交替分布组成的多层隐身层，利用有效介质近似理论等效出物性参数是各向异性和连续性分布的理想电磁隐身层材料，实现电磁波隐身。Daniel T 等[13]首次将介质层多层结构应用到声隐身领域，等效出密度各向异性的声学隐身层，实现了声隐身。为在设计和应用中简化声学隐身层的结构和降低隐身层制备成本，有必要研究隐身层结构对隐身层性能的影响。近年来，对不同隐身层结构的声学隐身性能的研究，已经取得了一系列有价值的成果。Daniel T等[14]研究了介质层的不同层厚比对介质层的材料物性参数的影响。Wei Q 等[15]研究了隐身层结构和声波频率对声学隐身性能和双工通信能力的影响。Jo C 等[16]在考虑了声速和阻抗匹配的情况下，研究了非完美隐身层结构的改变对声学隐身性能的影响。Zhang X D 等[17]研究了五模超材料的隐身层性能与层数和层厚的关系。Dutrion C 等[18]尝试应用双层弹性材料圆柱壳，通过降低散射的方法来实现声隐身。

本文首先基于变换声学和等效介质理论计算出声学隐身层的各层介质层的密度和声速，然后利用COMSOL 软件仿真了不同声学隐身层结构的散射声场，最后通过计算不同声学隐身层结构的散射截面来定量评估声学隐身层的隐身性能，并将计算结果进行对比分析。

1 隐身层材料密度及声速的计算

变换声学理论是通过不同空间之间的坐标变换关系，求出不同空间之间的物性参数变换关系，从而根据隐身物体的外形来设计声学隐身层[19-20]。如果要将一个半径为a 的刚性球通过内外半径分别为a 和b 的隐身层覆盖，并实现刚性球对声波的隐身，需要做如图1 所示的坐标变换，得到坐标变换关系r ′= f (r )。图中的f 变换表示将左图半径为b的圆形区域映射压缩到右图内、外半径分别为a 和b 的环形区域，隐身层分布区域即为此环形区域。左图为虚拟空间，坐标描述为( r ,θ )，右图为物质空间，坐标描述为(r' ,θ')。

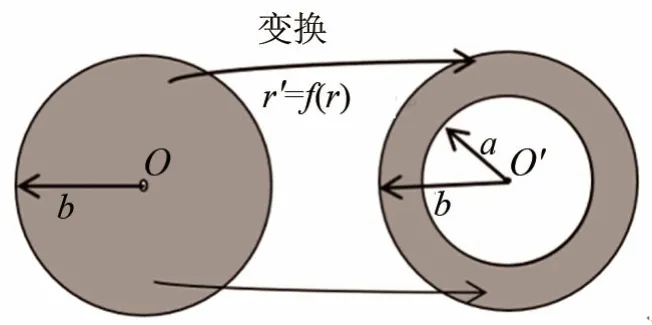
图1 坐标变换从O 到O'Fig.1 Transformation of coordinates from O to O'

两个区域都取极坐标系，它们之间的坐标变换f 可以描述为

原虚拟空间中极坐标系下的声学方程为

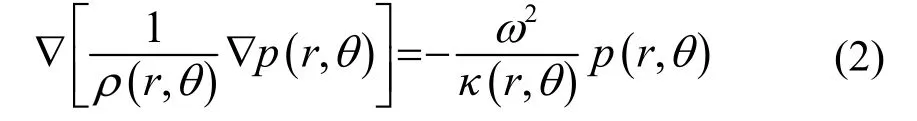
空间映射后物理空间中极坐标系下的声学方程为

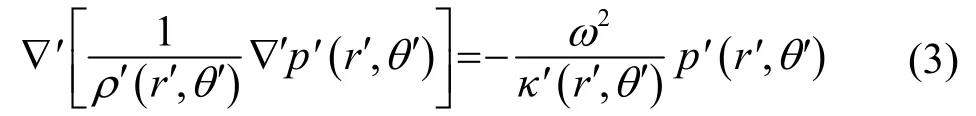
从上面的式(1)、(2)和(3)，可以得到物理空间和虚拟空间之间密度和体弹性模量的变换关系，如式(4)、(5)所示：

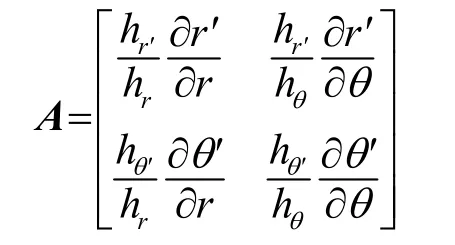
其中：hr,hθ和 hr', hθ'是坐标系的比例因子。极坐标系是正交坐标系，所以比例因子是hr=1 ，hθ= r = f (r')，且 hr' =1 , hθ'=r′。

将比例因子代入式(6)，可得：

将式(7)代入式(4)和式(5)，得到：

式(8)和(9)是矩阵形式的隐身层物性参数表达式，其标量形式的表达式如式(10)～(12)所示：

式(10)～(12)描述的声学隐身层物性参数(包括密度和体弹性模量)是非均匀、连续变化和各向异性的，在工程上很难实现，可通过多层结构等效得到，其等效物性参数可以利用等效介质理论近似计算得到[14]。隐身层由多层构成，其中每一层隐身层由两层不同材料参数的各向同性介质层组成。通过等效介质理论计算，多层的各向同性介质层可以等效出方向为r'和θ '的隐身层的有效密度ρr'和ρθ'，有效体弹性模量κ'。等效介质层组合示意图如图2 所示。

图2 等效介质层组合示意图Fig.2 The schematic diagram of equivalent medium layer combination

图2(a)描述了每一层隐身层由一层介质层A 和一层介质层B 组合而成。图2(b)描述了刚性球上覆盖的隐身层由多层介质层组成。第i 层隐身层中介质层A (i )和介质层 B (i )的密度和体弹性模量是ρA(i), ρB(i)和 κA(i),κB(i)。由介质层A 和B 组合而成的隐身层的有效密度和体弹性模量可以通过式(13)～(15)计算：

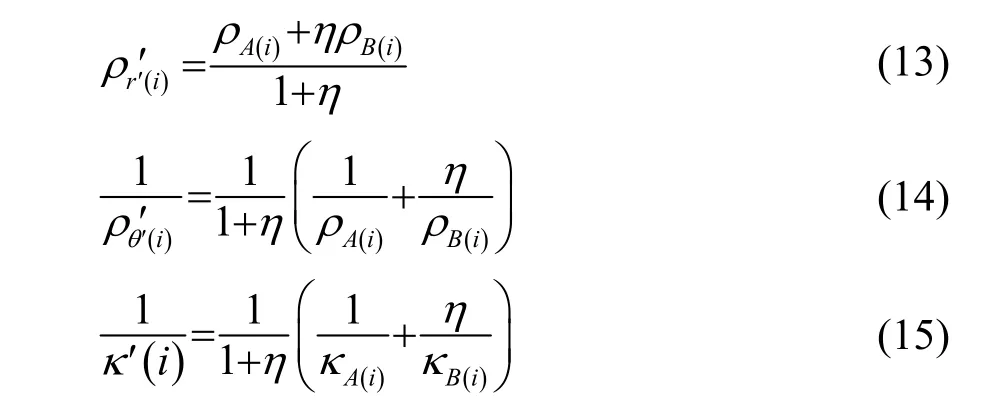
式中：η(i)=dA(i)/dB(i)，dA(i)和dB(i)分别是介质层A (i)和介质层 B (i)的厚度。

本文中取η(i)为常数，即η(i)=1，表示介质层A 和介质层B 的厚度相等。联立式(10)～(15)进行求解，可求得如式(16)～(18)所描述的每层隐身层的有效密度和体弹性模量：

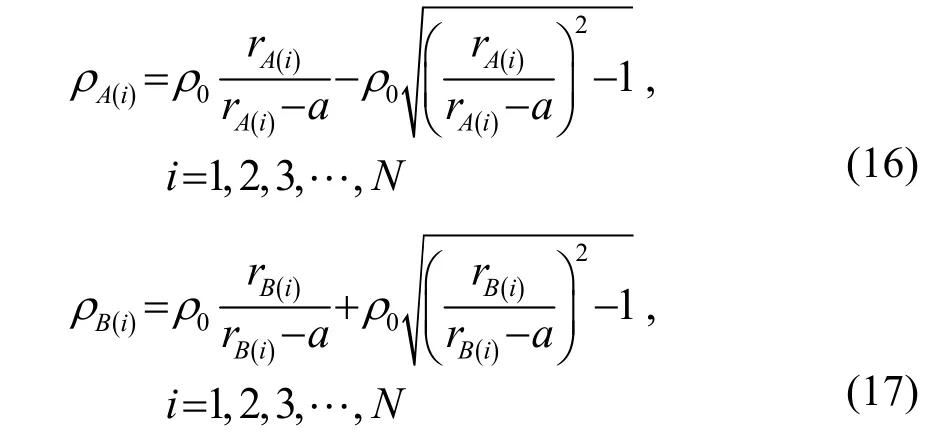
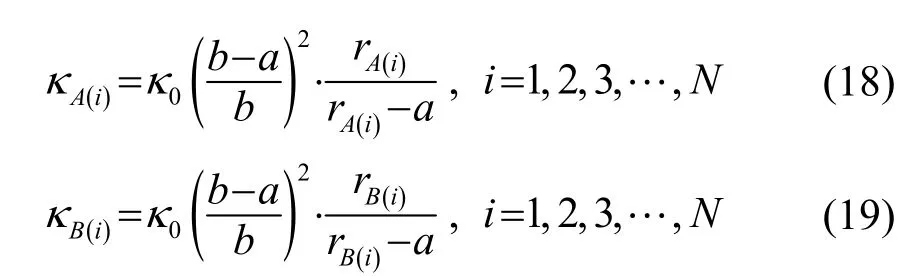
进而可以求得介质层中的声速：

式(16)～(19)中：ρA(i)和ρB(i)分别是第i 层介质的第A 层和第B 层的密度；cA(i)和cB(i)分别是第i 层介质的第A 层和第B 层的声速；ρ0是隐身层的外部介质密度；c0是隐身层的外部介质中声波传播的速度。rA(i)和rB(i)分别是第i 层介质的第A 层和第B 层半径，rA(i)、rB(i)取值范围是 a ≤rA(i),rB(i)≤b ，其中a为隐身层内径，b 为隐身层外径；κA(i)、κB(i)是隐身层的第i 层的第A 层和第B 层的体弹性模量。式(16)～(20)可以精确求得不同隐身层设计的每层介质层的有效密度、体弹性模量和声速。

2 计算分析模型和计算结果

2.1 计算分析模型

利用有限元软件COMSOL 对不同的声学隐身层结构进行计算分析，研究隐声层的结构对声学隐身性能的影响。建立的COMSOL 计算分析模型如图3 所示，模型中障碍物是半径为a 的无限长圆柱，声学隐身层内外半径分别为a 和b。声学隐身层覆盖在无限长圆柱表面，由多层介质层构成。介质层的密度和声速通过式(16)，(17)和(20)计算得到。示意图中半径为c 的圆环为设定的远场边界，半径为d 的圆环为计算区域边界。远场边界与计算区域边界之间的圆环区域为完美匹配层。

图3 计算模型示意图Fig.3 The schematic diagram of calculation model

计算分析模型中入射声波是平面简谐波，入射方向为从左向右。各个模型的入射波频率范围通过计算各个模型的kb 参数获得，参数取值范围是从kb=0.5 到kb=10(k 为波数，b 为声隐身层的外半径)，间隔取为0.5。在kb=0.5 到kb=10 的取值范围内，声学隐身层是有效的[21]。

分析模型中声学隐身层的周围介质是空气，密度ρ0是1.25 kg·m-3，空气中的声速c0是343 m·s-1，计算网格大小是0.000 1λ0(λ0是空气中声波的波长)。本文中隐身层覆盖的障碍物为半径为a=1 m，隐身层半径b 在不同的算例中取不同的数值，远场边界半径在图3 中取为c=2.5 m，在计算中设定为40 m，计算区域边界的半径在图3 中取为d=3 m。

对声散射的减缩效应进行定量分析的指标很多，包括散射截面、散射形函数和平均可视度[22]。本文中，用散射截面来定量评估隐身层的隐身性能。

无限长圆柱的散射截面定义为

其中， pi是入射声压， ps是散射声压。

2.2 计算结果

基于第1 节中的计算公式和分析模型，研究隐身层结构的总厚度、层厚和层厚分布等因素对隐身性能的影响。计算分析模型包括以下几种声学隐身层结构的设计方案：(1) 不同隐身层总厚度、相同层厚；(2) 相同隐身层总厚度、不同层厚；(3) 相同隐身层总厚度和相同层数而不同层厚分布。在每种方案中，分析模型参数值如表1、2 和3 所示。隐身层各介质层的密度和声速通过式(16)、(17)和(20)求得。把求得的密度和声速输入COMSOL 软件，计算不同声学隐身层结构设计方案中的声场分布。利用计算得到的声场分布，通过散射截面的计算公式，计算每个声学隐身层结构周围声场的散射截面，并将计算结果进行对比。散射截面对比图中的横坐标为参数kb。

2.2.1 总厚度对声学隐身层性能的影响

材料成本、制备难度或空间限制会影响隐身层的设计参数，是在隐身层应用中需要考虑的重要因素。下面对无限长圆柱覆盖4种不同厚度隐身层的声场分布进行计算，并对隐身层的散射截面进行对比分析。计算分析模型的参数如表1 所示。

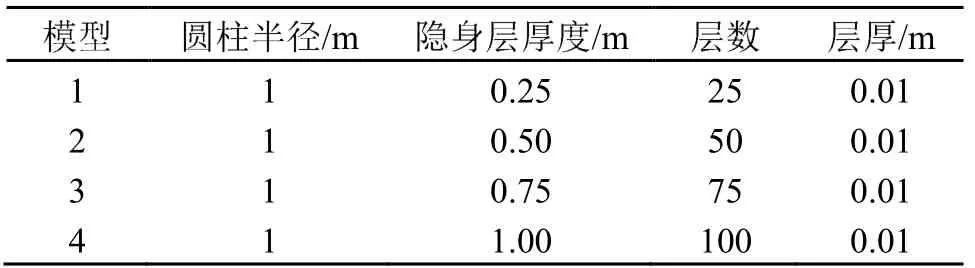
表1 不同总厚度隐身层的参数Table 1 Parameters of cloaking cover with different total thickness

图4 不同总厚度的隐身层的总声压场(kb=10)Fig.4 Total sound pressure fields of different total cloaking covering thicknesses (kb=10)

图4 为kb=10，b 从0.25～1.0 m 变化时的声场声压分布，b 从0.25 m 变化至1.0 m，相应的声波频率从440 Hz 变化至280 Hz。

图5 显示了4 种不同总厚度的隐身层的散射截面的对比结果。

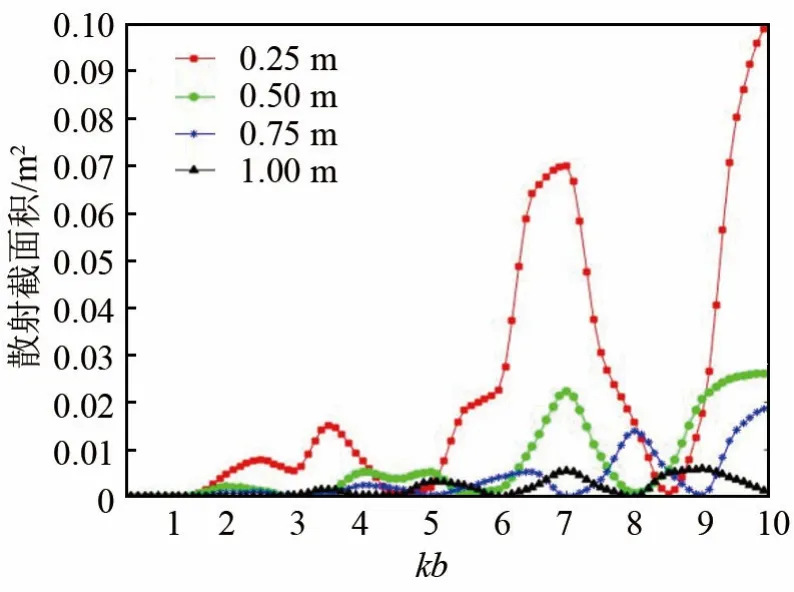
图5 不同总厚度的隐身层的散射截面对比Fig.5 Comparison between average visibilities of different total cloaking covering thicknesses

由图5 可知，1 m 厚度的隐身层的散射截面最小；0.75 m 和0.5 m 厚度隐身层的散射截面次之；0.25 m 厚度隐身层的散射截面最大。说明对于不同厚度的隐身层，厚度越大对声场的散射程度越弱，隐身性能越好，厚度越小对声场的散射程度越强，隐身性能越差。

2.2.2 层厚对声学隐身层性能的影响

为了在相同隐身层厚度条件下获得更好的声学隐身性能，需要研究在隐身层的总厚度不变情况下，改变各层厚度和层数对隐身层性能的影响。下面对5 种具有相同厚度、层厚均匀但不同层数的隐身层的声场声压分布进行计算分析。计算分析模型的参数取值如表2 所示。

表2 相同总厚度而不同层厚隐身层的参数Table 2 Parameters of cloaking cover with the same total thickness and different layer thicknesses

图6 为kb=10，b 保持0.5 m 不变，层数由20变化至80 时的声场声压分布。

图7 显示了相同总厚度情况下，5 种不同层厚和层数的隐身层的散射截面及对比。

由图7 可知，分层数为80 层的隐身层的散射截面最小，散射截面随层数减小逐渐变大，20 层介质层的隐身层的散射截面最大。说明对于总厚度确定、层数不同而层厚均匀的隐身层，层数越多对声场的散射程度越弱，隐身性能越好，层数越少对声场的散射程度越强，隐身性能越差。

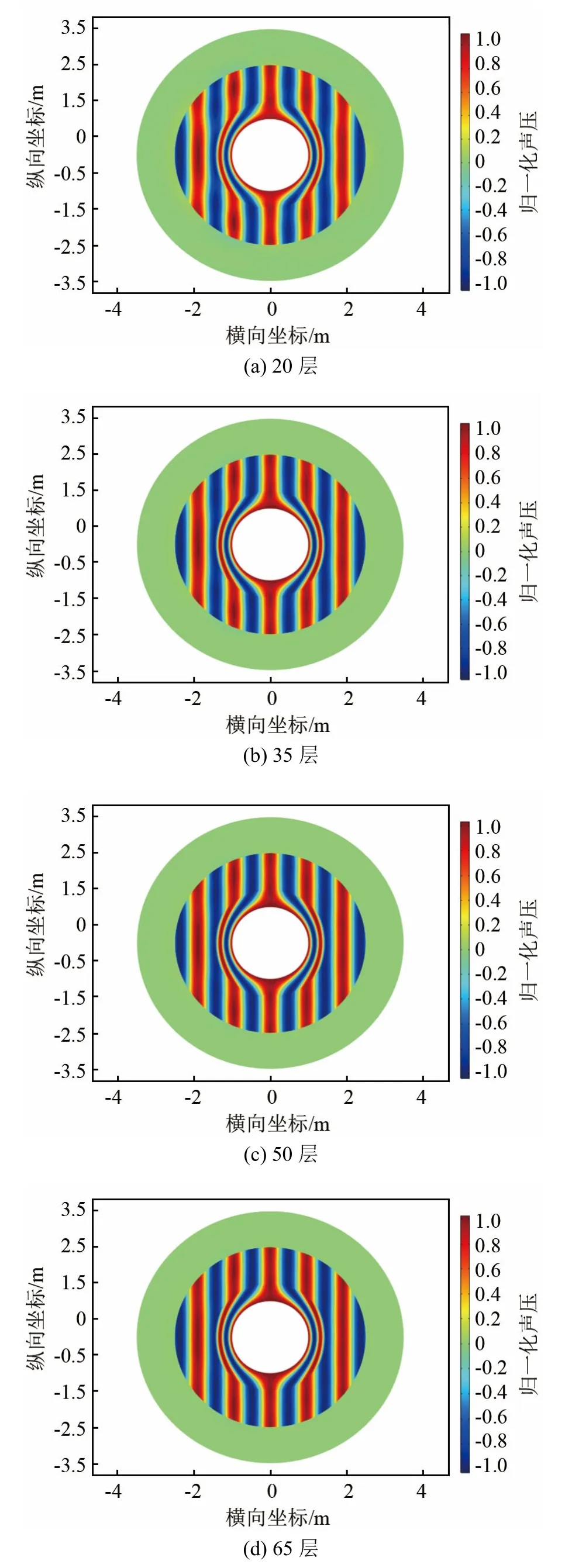
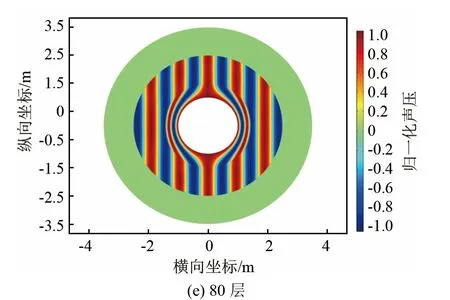
图6 相同总厚度不同层厚的隐身层的总声压场(kb=10)Fig.6 Total sound pressure fields of the same total cloaking covering thickness and different layer thicknesses (kb=10)

图7 相同总厚度而不同层厚的隐身层的散射截面对比Fig.7 Comparison bwtween average visibilities of the same total cloaking covering thickness but different layer thicknesses

2.2.3 层厚分布对声学隐身层性能的影响

增加隐身层的厚度意味着增加声学超材料的使用量，增大隐身层的分层数目意味着增大隐身层的制备复杂度。对于确定的隐身层厚度和层数的隐身层，研究如何在不增加声学超材料使用量和不增加制备复杂度的情况下，使隐身层具有更优良的隐身性能，在隐身层实际应用中具有重要的意义。下面对3 个具有相同总厚度和层数但不同层厚分布的隐身层的声场分布进行计算分析。

计算分析模型的参数如表3 所示。

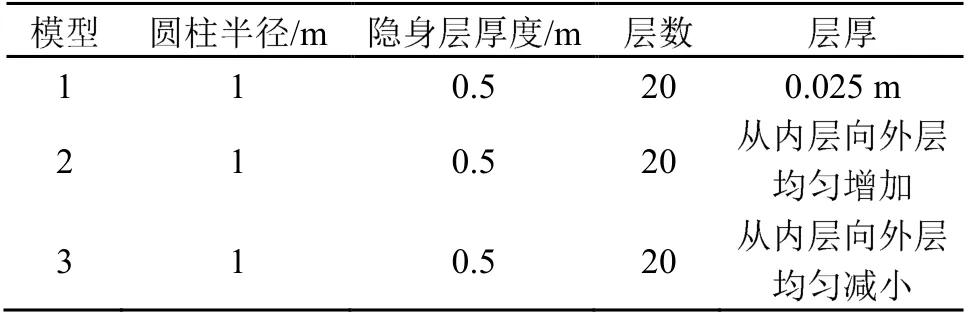
表3 相同总厚度和层数而不同层厚分布隐身层的参数Table 3 Parameters of cloaking cover with the same total thickness and layer number but different arrangements of layer thickness

图8 为kb=10、b=0.5 m、层数=20、不同层厚分布时的声场声压分布。

图9 显示了相同总厚度和层数情况下，3 种不同层厚分布的隐身层的散射截面及对比。

由图9 可知，相同总厚度和层数的情况下，外部层厚较薄而内部层厚较厚的隐身层散射截面最小，均匀层厚分布的隐身层散射截面次之，外部层厚较厚而内部层厚较薄的隐身层散射截面最大。说明对于总厚度和层数都确定的隐身层，层厚分布外部越薄的隐身层，隐身性能越好，层厚分布外部越厚的隐身层，隐身性能越差。

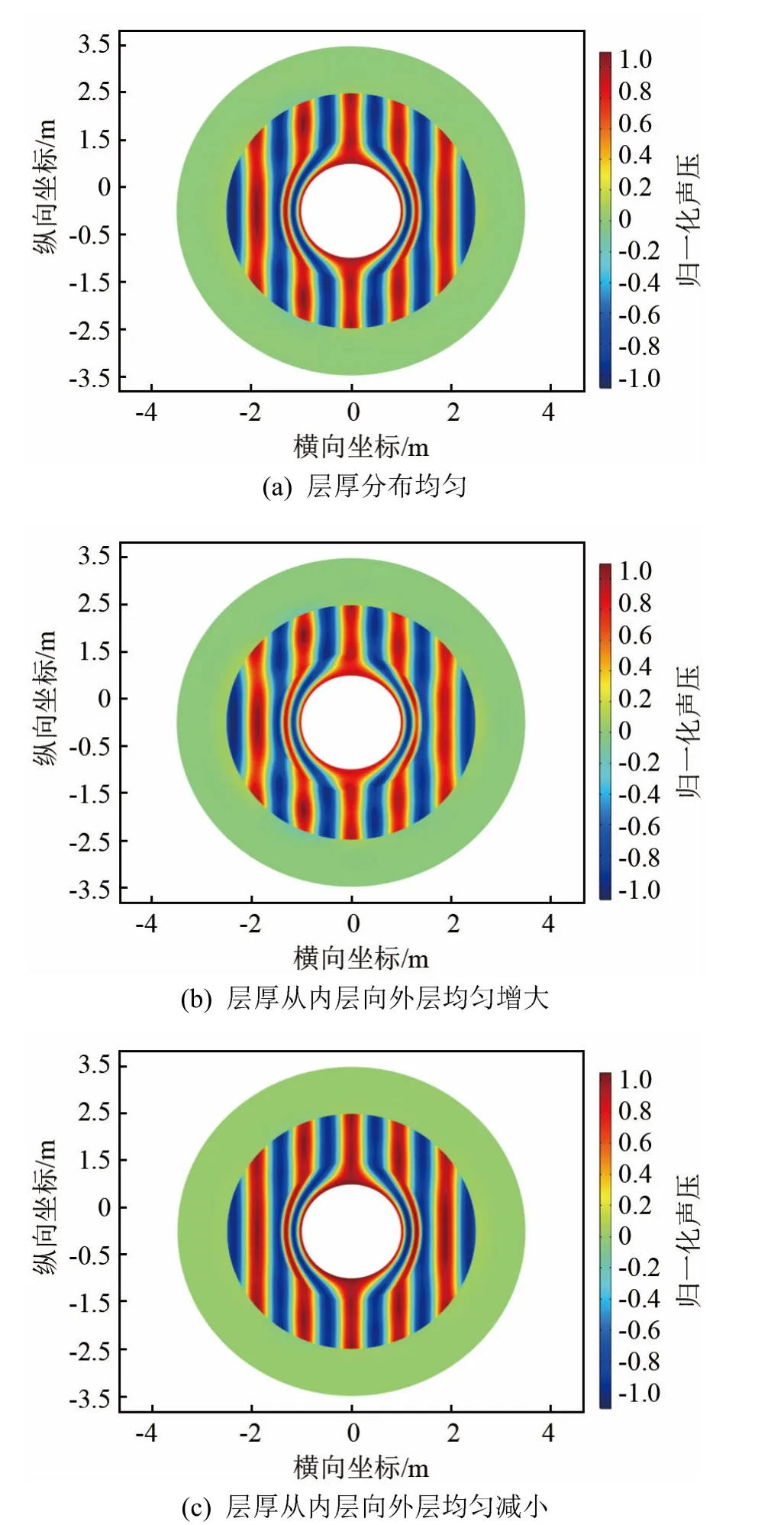
图8 相同总厚度和层数，不同层厚分布的隐身层的总声压场(kb=10)Fig.8 The total sound pressure fields of the same total thickness and layer number but different arrangements of layer thickness (kb=10)

图9 相同总厚度和层数而不同层厚分布的隐身层的散射截面对比Fig.9 Comparison between average visibilities of the same total thickness and layer number but different arrangements of layer thickness