轨道车辆制动系统轴套配合的工艺尺寸研究
2020-03-23王玥龙孙广合潘全章
王玥龙, 孙广合, 潘全章
(1 北京纵横机电科技有限公司, 北京 100094;2 中国铁道科学研究院集团有限公司 机车车辆研究所, 北京 100081)
在轨道车辆制动系统中,经常采用轴套配合的形式。尤其在控制系统阀类产品中,普遍采用铝制阀体压装不锈钢轴套的设计,轴套外径与阀体采用过盈配合,轴套内径与阀芯采用动配合的形式。
在产品设计中,通常只标注最终配合的尺寸及公差,以满足产品运用的要求。但是,由于轴套与阀体采用的是过盈配合,压装后轴套会产生收缩变形,如果轴套内径收缩量超过了阀芯间隙配合的公差,就极易导致阀芯的偏磨(见图1),影响产品性能。故需要在轴套压装完成后,再进行一序镗孔加工,考虑到二次装夹的影响,加工难度与成本较高。

图1 制动系统某种阀的阀芯发生偏磨现象
通过理论计算与有限元模拟两种方法,以城轨制动控制装置某阀件的轴套为研究对象,分别计算轴套压装后的内径收缩量,并与实际测量值进行对比分析。再以收缩量为依据,根据工程应用的不同要求,提出3种评估方法确定工艺尺寸,保证压装后的轴套配合满足产品运用的要求,省去了镗孔工序,提升了产品生产效率,降低了制造成本。
1 问题描述
选取城轨制动控制装置中某阀的轴套为研究对象。如图2所示,其中:1为阀体,2为轴套,3为阀芯。

图2 阀体轴套配合示意图
轴套为不锈钢材质,阀体为铸铝材质,轴套外径与阀体采用过盈配合,轴套用压力机常温等速缓慢压装入阀体。轴套内径与阀芯采用间隙动配合,阀芯在输入空气压力的作用下往复运动。
根据零件结构与压装过程,将实际模型简化为光滑圆柱过盈配合连接,如图3所示。相关参数见表1。

图3 阀体轴套配合简化视图

表1 实例基本参数表
根据简化后的模型,通过理论计算和有限元模拟两种方式,研究过盈量与内径收缩量的关系,从而得到内径收缩量的计算方法,再根据内径收缩量对内径工艺尺寸进行评估确定。
2 理论计算
关于轴套配合的理论计算,主要参照标准GB/T 5371-2004《极限与配合 过盈配合的计算与选用》,要求是光滑圆柱面在弹性范围内的过盈联结计算。
标准的计算,要求轴套满足:
(1)包容与被包容件的结合应力和应变在线弹性范围内;
(2)配合处于平面应力状态,且结合压力为常数;
(3)材料弹性模量为常数;
计算的强度理论是按照变形能理论。
2.1 计算方法
结合应力Pf为:
(1)
其中:δ为过盈量;df为结合直径;Ea为基体弹性模量;Ei为轴套弹性模量。
系数Ca和Ci分别为:

(2)
其中:基体直径比qa=df/da;轴套直径比qi=di/df;da为基体外径;di为轴套内径;νa为基体泊松比;νi为轴套泊松比。
则轴套的内径收缩量Δdi为:
(3)
取k为内径收缩率,则:
(4)
即可得到内径收缩量Δdi与过盈量δ的线性函数关系Δdi=k·δ。
2.2 实例计算
(1)基本参数:选取第1节中的问题实例,进行计算,相关参数定义如表2。

表2 理论计算基本参数
(2)实例参数:
随机选取5件阀体与轴套作为样本,实际测量参数(此处轴套内径为已经调整工艺尺寸后的内径值),计算得到实际过盈量,如表3所示。

表3 理论计算实例参数
2.3 计算结果
根据表1和表2的参数值,按照式(1)和式(3)计算得到结合应力与轴套内径收缩量,再结合压前的轴套内径尺寸,即可进一步得到理论计算的压装后轴套内径尺寸,见表4。
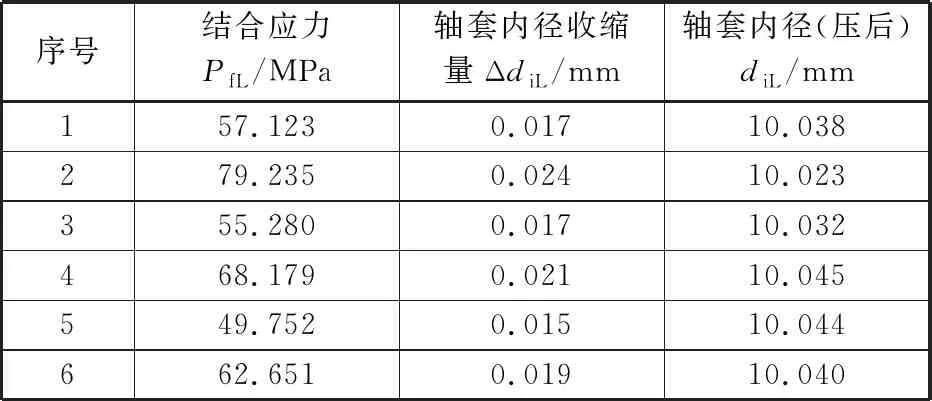
表4 理论计算实例计算结果
从表4计算结果可以看出,依据过盈量的大小,轴套内径的收缩量在0.015~0.024的范围内,由于压前尺寸已经根据经验进行了调整,所以理论计算的压后尺寸整体偏大,保证了与阀芯的动配合间隙。
最后根据式(4),即可计算得到内径收缩率为k=0.561。
3 有限元模拟
通过第2节的前提条件可以发现,理论计算内径收缩量,要求轴套与基体必须为光滑圆柱结构,这就限制了其应用的范围,对于异形结构的基体或轴套将无法通过理论计算得到。
这时,就需要通过有限元法来模拟轴套配合的结构形式,仿真计算出内径的变形量。通过SolidWorks Simulation建立第1节问题的有限元模型,计算不同的过盈量下的轴套内径收缩量,从而得到压装后轴套内径尺寸。
3.1 模型建立
选取第1节中的问题实例,材料属性按照表2参数设置,选取表3中的3号样本进行示例模拟分析。阀体基孔尺寸为12.015 mm,轴套外径为12.045 mm,过盈量为0.030 mm,压前轴套内径尺寸为10.049 mm。
根据结构的轴对称特性,将模型进行简化,选择结构1/4部分构建几何模型。在圆柱坐标系下,施加轴对称约束,定义接触方式为冷缩配合,控制接触面网格的精度,进行求解。
3.2 有限元结果
经过对有限元模型的计算,可以得到基体与轴套间的径向应力和轴套内径表面节点位移,在圆柱坐标系下,径向应力即为结合应力,轴套内径表面节点位移平均值的2倍即为轴套内径收缩量,如图4~图5所示。
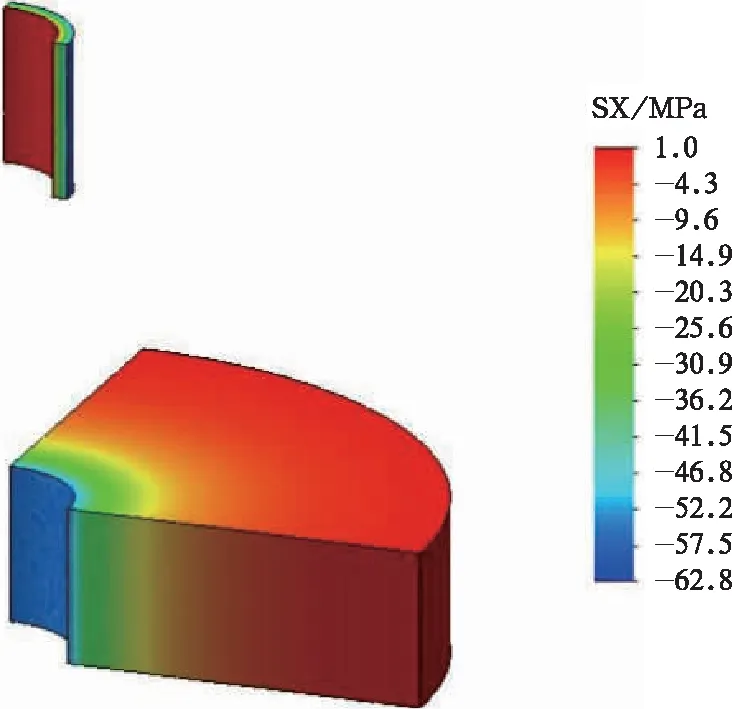
图4 轴套配合结合应力
选取径向应力单元平均值作为结合应力值PfF=52.795 MPa。轴套内径表面节点位移平均值为0.008 43 mm,则轴套内径收缩量ΔdiF=0.008 43×2=0.016 9 mm,进而可计算出压装后轴套内径尺寸diF=10.032 mm。
按照相同方法,可计算出表 3中6个样本的有限元计算结果,如表5所示。
4 结果分析
为了验证两种计算方法的结果,将6组样本分别进行压装后,测量其内径的值,并根据压前内径尺寸计算得到轴套内径收缩量的测量值,并与理论计算、有限元计算的结果进行对比分析。如表6所示。
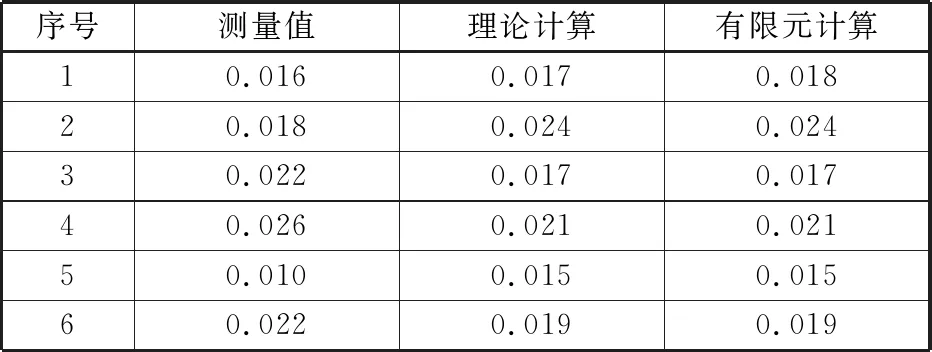
表6 测量值、理论计算和有限元计算的内径收缩量对比 mm
由于实际压装过程中,轴套是由压力机垂直压入阀基体,故测量值存在一定的离散性。根据理论分析,轴套内径压后尺寸与过盈量是线性关系,为消除小样本离散性对结果的影响,故将实际测量值进行一元线性回归后,与理论计算、有限元计算结果进行对比分析,如图6所示。

图6 测量值、理论值与有限元值结果对比图
通过对比可以发现,理论计算与有限元计算的结果基本一致,两种计算方法所得到的内径收缩量与实际测量值的回归分析结果也基本一致,平均相对误差分别为2.91%和2.90%。
所以,这两种方法均可以有效的计算轴套配合的内径收缩量,并以此为依据,进行工艺尺寸的评估。
5 工艺尺寸的评估
从第4节的结果对比可以发现,理论计算与有限元计算的结果均较为准确,符合工程应用的条件,由此便得到了计算轴套内径收缩量的两种方法。
内径收缩量的计算是正确评估压装工艺尺寸的前提,以此为依据,根据工程应用的不同特点,提出了3种确定压装前轴套内径工艺尺寸的方法,分别为修配法、间隙优先法和概率法。
(1)修配法
在轴套内径加工前,通过测量基体内径和轴套外径确定实际过盈量,计算得到内径收缩量,以此为依据得到的压前内径工艺尺寸是最为准确的。

(2)间隙优先法
在工程应用中,内径轴孔配合存在优先保证间隙的情况,即要求配合轴转动灵活,此时可以以最大内径收缩量为依据,进行轴套内径压前工艺尺寸的计算。

(3)概率法
上述两种方法在使用上都存在一定的局限性,故在保证工程应用便捷性和压后尺寸精度的前提下,提出一种更为通用的方法。
在机械加工中,工件的尺寸误差是由很多相互独立的随机误差综合作用的结果,如果其中没有某种随机误差起决定性作业,则加工后工件的尺寸将符合正态分布,即:
X~N(μ,σ2)
(5)
其中:X为加工尺寸;μ为期望值;σ为标准差。
根据机械加工的特点,可以分析出μ反映机床调整尺寸,σ反映机床的加工精度。想要得到加工尺寸的分布,需要大量的样本对期望与方差进行参数估计。这里,为了工程应用的便捷性,可以根据“3σ原则”,进行设定。
μ=(2X+ES+EI)/2,σ=(ES-EI)/6
(6)
按此方法,可以得到基体内径dfw,轴套外径dfn和轴套内径di的分布。
根据第2节理论分析的结果,轴套内径的压前工艺尺寸digy是基体内径dfw、轴套外径dfn和轴套内径di的线性函数,即:
digy=di+k·δ=di+k·(dfn-dfw)
(7)
由于各尺寸都是相互独立的随机变量,则其线性组合也符合正态分布,从而得到压前工艺尺寸的概率分布:
(8)
再根据3σ原则确定公差等级,从而得到压前工艺尺寸。
6 实例应用分析
6.1 实例计算
(1)修配法


表7 修配法计算结果
(2)间隙优先法

(3)概率法
按照实例,可以计算得到相关分布参数,见表8。
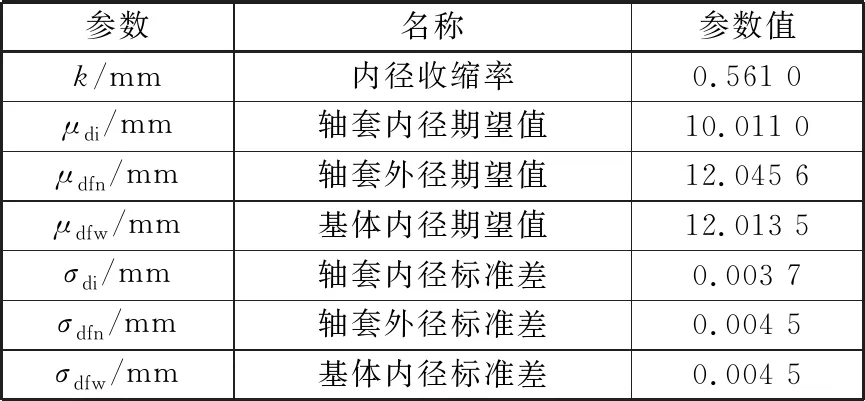
表8 理论计算 基本参数
根据式(8)计算得到轴套内径的压前工艺尺寸分布,期望值μdigy为10.030 mm,标准差σdigy为0.005 1 mm,分布如图7所示。
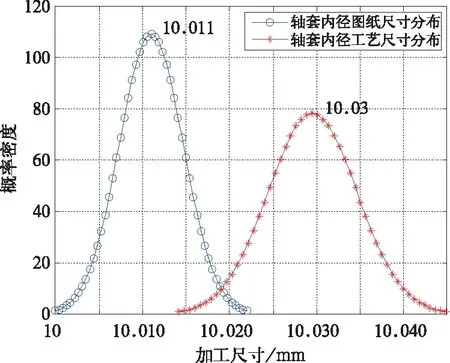
图7 轴套内径图纸与压前工艺尺寸分布图
从而计算得到轴套内径工艺尺寸的上极限尺寸10.045 mm,下极限尺寸10.014 mm,公差带为0.031 mm。
6.2 应用分析
将上述3种方法的评估结果进行对比,如表9所示。

表9 3种评估方法的结果对比表
通过对比可以发现,修配法和间隙优先法保持了原尺寸公差带,概率法由于根据“3σ原则”重新定义了尺寸分布,公差带有所增加,3种方法均没有提高公差等级,故加工难度没有增加。间隙优先法的评估尺寸较修配法和概率法有所增大。
综合3种方法的理论依据和计算结果,将其应用特点分析如下:
(1)修配法:需要单独测量每个工件的压前配合尺寸,并依据实际过盈量进行工艺尺寸的评估,结果最为准确,但生产效率较低,适用于小批量生产。
(2)间隙优先法:根据计算结果可以发现,该方法的评估尺寸最大,保证了在最大过盈量压装后,仍能实现间隙动配合,故其评估准确性较低,但该方法评估过程简单,工程应用便利性较高,适用于动配合间隙较大或优先保证间隙的情况。实例中采用该方法进行评估后,取得了较好的工程应用效果。
(3)概率法:该方法运用机加工概率分析进行工艺尺寸的评估,从理论上保证了结果具有较高的准确性,通过实例计算,评估的尺寸公差带有所增加,降低了加工难度。但该方法计算较为复杂,需要机床加工尺寸符合正态分布。如果实际机床加工存在其他形式的波动,还需要先通过取样进行参数估计,得到准确的尺寸分布后,再进行评估。
7 结 论
以轨道车辆制动控制装置中某阀的轴套配合为实例,通过理论计算和有限元模拟两种方法,计算出压装后轴套内径收缩量,分析得到内径收缩量与压装过盈量的线性关系,从而得到内径收缩量和内径收缩率的计算方法,并与实际测量值进行对比分析,验证了计算方法的准确性,为评估轴套压前工艺尺寸提供了基础。
根据工程应用的不同情况,提出了3种工艺尺寸的评估方法。针对小批量生产,可以采用修配法,按照单个产品进行控制,实现最好的评估效果。针对优先保证间隙的情况,可以采用间隙优先法,保证在最大压装过盈量的情况下,轴套内径仍能满足间隙配合。针对更加普遍的情况,提出了概率法,依据工程应用“3σ原则”,计算得到轴套压后工艺尺寸的概率分布,实现工艺尺寸准确性和工程应用便捷性的统一。
通过上述两个步骤,即可评估计算出轴套内径压前工艺尺寸,保证压装后的产品符合配合要求,省去了2次加工,提升了产品生产效率,降低了制造成本。
