基于MMI-PCA-KLPP二次降维和模糊树模型的NOX浓度软测量方法
2020-03-11刘长良王梓齐
刘长良, 曹 威, 王梓齐
(1.华北电力大学 控制与计算机工程学院,河北 保定 071003; 2.华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引 言
火力发电是我国主要的发电形式,燃煤产生的氮氧化物成为空气污染的主要因素[1]。然而气体分析仪对NOX的测量存在滞后,严重影响了脱硝系统的控制品质。因此,高精度的NOX软测量方法对提高脱硝系统控制品质,减少氮氧化物排放有着重要意义。
NOX软测量方法主要有神经网络法、支持向量机法和组合预测方法等。白建云等将BP神经网络用于硫化床锅炉NOX软测量,大大减小了传感器测量的迟滞,改善了脱硝系统的控制品质[2];王雅彬等在分析了NOX排放量影响因素的基础上,构建了基于最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)的NOX排放软测量模型,提高了NOX的测量精度[3];丁知平等对基于LSSVM的NOX软测量模型采用改进引力优化算法(Improved Gravitation Optimization Algorithm,IGSA)进行优化[4];石饶桥等提出基于卡尔曼滤波与数据融合技术的NOX浓度测量方法,有效克服测量滞后问题,并具有较快的测量响应速度和较高的测量精度[5]。上述NOX软测量方法均实现了减小测量迟滞、提高测量精度的目的,但是机器学习算法普遍存在训练时间长、泛化能力差等问题。
针对这一问题,毛剑琴等提出了一种基于二叉树结构的模糊T-S模型建模算法,简称模糊树模型(Fuzzy Tree,FT)[6]。模糊树模型有着结构简单、训练快、泛化能力强等优点,适用于非线性、强耦合的复杂工程问题[7]。Zhang等人基于模糊树模型建立了硫化床锅炉SO2软测量模型,准确预测了SO2排放量并基于模糊树算法建立了NOX和SO2软测量模型,对燃烧异常情况进行检验,验证了模糊树软测量模型的有效性[8,9];王梓齐等提出采用复相关系数的时滞联合估计方法,对影响NOX生成量的模型输入变量进行时滞估计,最后基于模糊树模型建立了SCR反应器入口NOX生成量动态模型[10]。
除此之外,由于选择性催化还原器(Selective catalytic reduction,SCR)入口NOX浓度受到机组负荷、烟气温度、烟气流量、烟气含氧量等多种因素影响,导致模型的输入变量较多,增加了模型的训练时间,因此有必要对模型的输入变量进行降维。董泽等人采用互信息(Mutual Information,MI)对NOX软测量模型的输入变量进行筛选[11];赵文杰等人利用互信息不仅筛选出了影响NOX浓度的主要变量,还实现了对输入变量的时滞估计,提高了模型的精度[12];赵建军等提出了基于核主元分析和LSSVM的SCR入口NOX浓度软测量方法,有助于解决SCR入口NOX浓度的准确测量问题[13]。上文献中利用互信息均实现了从众多影响因素中筛选主要影响变量的目的,但是由于NOX的生成机理复杂,影响因素众多,导致互信息筛选后仍有较多输入变量的问题。针对这一问题应该对筛选后的变量进行二次降维,进一步减少输入变量数量。
局部保持投影(Locality Preserving Projection,LPP)可以在降低空间维度的同时,较好的保持内部固定的局部结构。马玉鑫基于LPP对输入变量进行降维,提取出有效的低维特征后再用LSSVM建立预测模型[14];张云强等人基于Parzen窗和成对约束的半监督局部保持投影算法对磨粒图像的纹理特征降维[15]。LPP虽然可以达到降维的目的,但是LPP的本质是对拉普拉斯特征映射方法的线性逼近,对于非线性强的系统有效性差。另外,LPP仅仅考虑了样本的局部结构特性,并未考虑样本的全局结构特性。主元分析法(Principal Component Analysis,PCA)在降维时考虑了样本的全局结构特性,综合PCA 与LPP 的特点,可以在降维过程中同时保持数据样本的局部结构特征和全局结构特征[16]。
针对机器学习算法存在训练时间长和LPP对非线性系统降维有效性差的问题,首先通过查阅文献大体确定NOX软测量模型的输入变量;再利用核方法将LPP推广到适用于非线性系统的KLPP(Kernel LPP,KLPP),并将KLPP与PCA相结合,以达到同时保持样本的全局结构特性和局部结构特性的目的;最后基于模糊树算法建立NOX软测量模型。应用某600 MW燃煤机组的实际运行数据对该NOX软测量方法进行了实验验证,实验结果表明,该方法满足实际对SCR入口NOX软测量的要求。
1 互信息降维
互信息是定量计算两个随机变量之间共有信息量的计算工具,是表示两个随机变量相关性的有效值指标。互信息的算法如下。
两个随机变量X、Y的互信息为
(1)
式中:P(x,y)为X、Y的联合分布;P(x)、P(y)分别为X、Y的边界分布。然而公式(1)只考虑了两变量之间的最大相关,并没有考虑信息冗余。因此又提出了一种最大相关、最小冗余的变量筛选法,该方法的评价函数如下:
(2)
式中:fi∈F为待选变量;β为惩罚因子,主要是用来调节候选变量与各个已选变量之间的互信息之和;c为主导变量;sj∈S为已选变量。但是公式(2)没有考虑到已选变量个数对算法的影响,因此导致互信息筛选后可能还有较多变量。所以在公式(2)的基础上加入已选变量数目的惩罚因子进行改进,改进后的评价函数如下:
(3)
式中:‖S‖为S的范数。从式(3)可以看出,改进后的算法考虑到了变量数目的影响,将已选变量数目的影响作为惩罚项加入到评价函数中,除以|S|可以减小待选变量与主导变量的互信息对变量重要性的影响,从而控制了互信息筛选出的变量数目。
改进互信息(Modified Mutual Information,MMI)的具体步骤如下:
(1)初始化:F为所有待选变量集合;已选变量S为空集;c为主导变量,即SCR入口NOX浓度;
(2)计算待选变量fi与主导变量c的互信息I(fi;c),选择最大I(fi;c)对应的fi存入S中并从F集合中删除fi;
(3)循环以下两个步骤,直至已选变量数目达到预测值K:
(a)计算所有待选变量与已选变量的互信息I(fi;sj);
(b)选取使评价函数J(fi)最大的fi,并存入S;
(4)已选变量集合S即为模型的输入变量。
MMI算法的流程图如图1所示。

图1 MMI 降维流程图 Fig.1 Flow chart of MMI dimension reduction
2 PCA-KLPP降维
PCA-KLPP降维法综合了PCA和KLPP两种降维法的优势,全面考虑了样本的局部结构特性和全局结构特性,不仅可以将同类样本按流形投影到低维空间,还可以保证异类样本间的分散性,避免了不同类别而又靠得较近的数据在投影后还是靠得较近的问题。
设X={x1,x2,…,xm},xi∈Rd(i=1,2,…,m)为高维空间Rd中的样本,PCA-KLPP的目标是找到一个转换矩阵W,将X在低维空间Rl(l< PCA-KLPP降维法的整体目标函数是基于KLPP的局部目标函数和PCA的全局目标函数,从而使得整体目标函数兼具KLPP和PCA的优势。 由于PCA 在降维时考虑了样本的全局结构特性,因此,全局目标函数Jg(W)即为PCA-KLPP降维法的全局目标函数。Jg(W)使投影前分散的两点投影后仍保持分散,避免了LPP将高维空间中不同类但靠得近的数据投影到低维空间中相邻的问题。Jg(W)目标函数如下: (4) 由于KLPP 在降维时考虑了样本的局部结构特性,因此,局部目标函数Jl(W)即为PCA-KLPP降维法的局部目标函数。Jl(W)使投影前近邻的数据投影后依然相邻,保持数据结构相似[17]。Jl(W)目标函数如下: (5) (6) (7) 其中,sij为近邻的第i个样本和第j个样本之间的相似性程度;矩阵D是对角阵,对角元素dii为 (8) 为了消除随机尺度因子的影响,求解中限定: WTXDXTW=I (9) 式中:I为单位矩阵。 结合全局目标函数Jg(W)与局部目标函数Jl(W),构造PCA-KLPP的整体目标函数如下: (10) 用拉格朗日法根据上式构造极值函数为 (11) 对上式求导并置0,化简后得 L′(W)=2(C-XLXT)W-2λXDXTW=0 (12) (C-XLXT)W=λXDXTW (13) 从式(13)可以看出,求转换矩阵W的过程,实际上是求以λ为广义特征值的特征向量的过程。因此求出W后,便可实现降维的目的。PCA-KLPP 降维算法的基本流程如图2所示。 图2 PCA-KLPP 降维流程图Fig.2 Flow chart of PCA-KLPP dimension reduction 模糊树算法的核心是用二叉树将输入空间划分成模糊子空间,二叉树的结构决定了模糊规则的个数,并且模糊规则不受输入变量维数的影响,因而不会导致“维数爆炸”。 对于一个模糊树模型,对应着一个严格二叉树T。T中共有L个节点,对于每个节点t,定义其隶属度函数为μt(x)。对于根节点,μt(x)=1;对于非根节点,μt(x)的计算公式如下: (14) (15) 式中:α为模糊带宽度;t为F(t)的右子节点α>0;CF(t)为F(t)上的线性参数向量Ct;θF(t)为F(t)上的数据重心,计算公式如下: (16) (17) 式中:Nt(x)为节点t的归一化隶属度函数 (18) 经过训练得到各节点上的线性参数向量Ct以及数据重心θt后,便确定了一个模糊树模型。 首先通过查阅资料,大体确定影响SCR入口NOX浓度的影响因素,从而确定软测量模型的输入变量;由于输入变量维数过多,先采用MMI方法对输入变量进行一次降维,对一次降维后的变量再采用PCA-KLPP方法进行二次降维,在确定最佳维数的前提下,既保了留原始数据的结构特征,又大大减少了模型输入变量的数目,缩短了软测量模型训练时间;最后对二次降维后的数据建立模糊树模型,对NOX浓度进行预测。MMI-PCA-KLPP二次降维的NOX软测量流程图如图3所示。 图3 二次降维和FT的NOX软测量流程图Fig.3 Flow chart of secondary dimensionality reduction and FT 通过相关资料,得知影响NOX浓度的主要因素。由于在平稳工况下,A磨未启动,A磨风量、煤量、及一二次风门开度均为0,故将以上变量从辅助变量中剔除,剩下的辅助变量如表1所示,共30个输入变量,输出变量为SCR入口NOX浓度。其中,T1为空预器一次风温;T2为空预器二次风温;SA~SE、SAA~SDE为各二次风门挡板开度;SOFA1~SSOFA3为各燃尽风门开度;O2为烟气含氧量;从而确定软测量模型的输入变量[18]。 采集某660 MW燃煤电厂SIS系统中26 h运行数据,采样间隔为10 s,共8 640组。NOX浓度和机组负荷时间序列如图4。选取第3 501~8 550组稳定工况下的数据,选择前4 500组作为训练样本,后650组作为测试样本。平稳工况下的NOX浓度和机组负荷时间序列如图5所示。 图4 NOX浓度和机组功率时间序列Fig.4 NOX concentration and unit power time series 图5 平稳工况下NOX浓度和机组功率时间序列Fig.5 NOX concentration and unit power time series under steady conditions 由于MMI和PCA-KLPP两种方法需要先验确定样本所要降低的维数,维数降低过多会导致样本失去本身的数据特征,过少则不能达到简化软测量模型缩短训练时间的目的。因此,合理的维数是建立软测量模型的关键。本文依次计算30维辅助变量与主导变量NOX浓度的互信息值,将30个互信息从大到小排序,寻找互信息曲线的拐点,从而确定MMI降维法的最佳维数。图6为维数从1到30时互信息值变化情况及曲线拐点。 图6 各变量互信息值与最佳维数Fig.6 Mutual information value and optimal dimension of each variable 从图6可以看出,不同辅助变量与主导变量的互信息值不同,说明各辅助变量与主导变量的相关性不同。除此之外,拐点对应的维数为26,从而确定降维后的输入变量数目为26。 再根据MMI降维后的26维辅助变量,计算26维辅助变量的特征值。由于特征值的大小代表了矩阵正交化之后所对应特征向量对于整个矩阵的贡献程度,因此将26维辅助变量的特征值按大小排序,寻找特征值大于阈值的变量(阈值这里取0.98),从而确定PCA-KLPP降维法的降维数目。图7为26维辅助变量的特征值曲线及最佳维数。 图7 各变量特征值与最佳维数Fig.7 Characteristic value and optimal dimension of each variable 从图7可以看出,不同辅助变量的特征值大小不同,说明辅助变量对主导变量的贡献程度不同。并且特征值曲线的拐点出现在维数为12,因此确定PCA-KLPP二次降维的最佳维数为12,再用模糊树模型建立NOX软测量模型。 模糊树模型的精度受树结构的影响,复杂的树结构虽然会提高精度,但也会增加模型的训练时间。因此用模糊树模型建立NOX软测量模型之前,必须确定合适的树结构。表2为不同树结构下软测量模型的精度和训练时间,RMSE为训练误差。 表2 不同树结构下模型的精度和训练时间 Tab.2 Model error and training time of models under different structures 树结构1层1节点2层3节点3层5节点3层7节点RMSE3.683.573.193.17t/s5.0644.74103.48274.56 从表2可以看出,当树结构为2层3节点时,模型兼具了精度高和训练时间短的优点,因此本文采用树结构为2层3节点的模糊树模型。除此之外还可以看出,模糊树模型对非线性系统有良好的适用性并且精度高。图8为FT、MI_FT和二次降维-FT三种模型训练预测值与实际值拟合图,图9为二次降维-FT的测试结果。 图8 训练样本预测值与实际值拟合图Fig.8 Fitting predicted and actual values of training samples 图9 二次降维-FT软测量模型的测试曲线Fig.9 Test curve of the second dimension reduction-FT model 图8可以看出,三种模型预测值均紧贴理想直线,说明三种模型能准确测量NOX浓度,但是二次降维-FT模型的精度低于FT模型。为了进一步研究几种模型的训练时间及模型误差,表3列出了三种模型的训练时间与误差。其中,RMSE1为训练误差,RMSE2为测试误差,t为训练时间。 表3 几种模型的误差与训练时间 表3可以看出,虽然二次降维-FT模型在软测量精度上与FT模型有差距,但是两者精度相差不大,并且模型训练的时间较FT大大缩短,误差也在工业可接受范围,可以很好地解决NOX测量大迟滞的问题。 针对火电厂气体分析仪测量存在滞后和NOX软测量不准确的问题,提出了一种基于MMI-PCA-KLPP二次降维和FT的SCR入口NOX浓度软测量方法。首先查阅文献,大体确定软测量模型的输入变量;再依次确定MMI和PCA-KLPP两种降维方法的最佳维数,并用这两种降维方法依次对原始数据进行降维;最后选择最佳的模糊树结构,建立了SCR入口NOX浓度软测量模型。实验结果表明,基于二次降维后,能在精度降低不多的情况下,大大缩短模糊树模型的训练时间,满足实际工程中NOX软测量的要求。2.1 全局目标函数
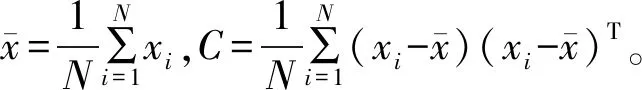
2.2 局部目标函数
2.3 整体目标函数
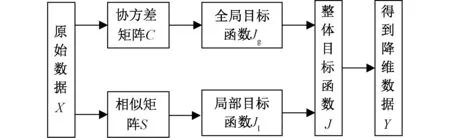
3 软测量模型
3.1 模糊树模型
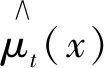
3.2 基于MMI-PCA-KLPP二次降维的NOX软测量
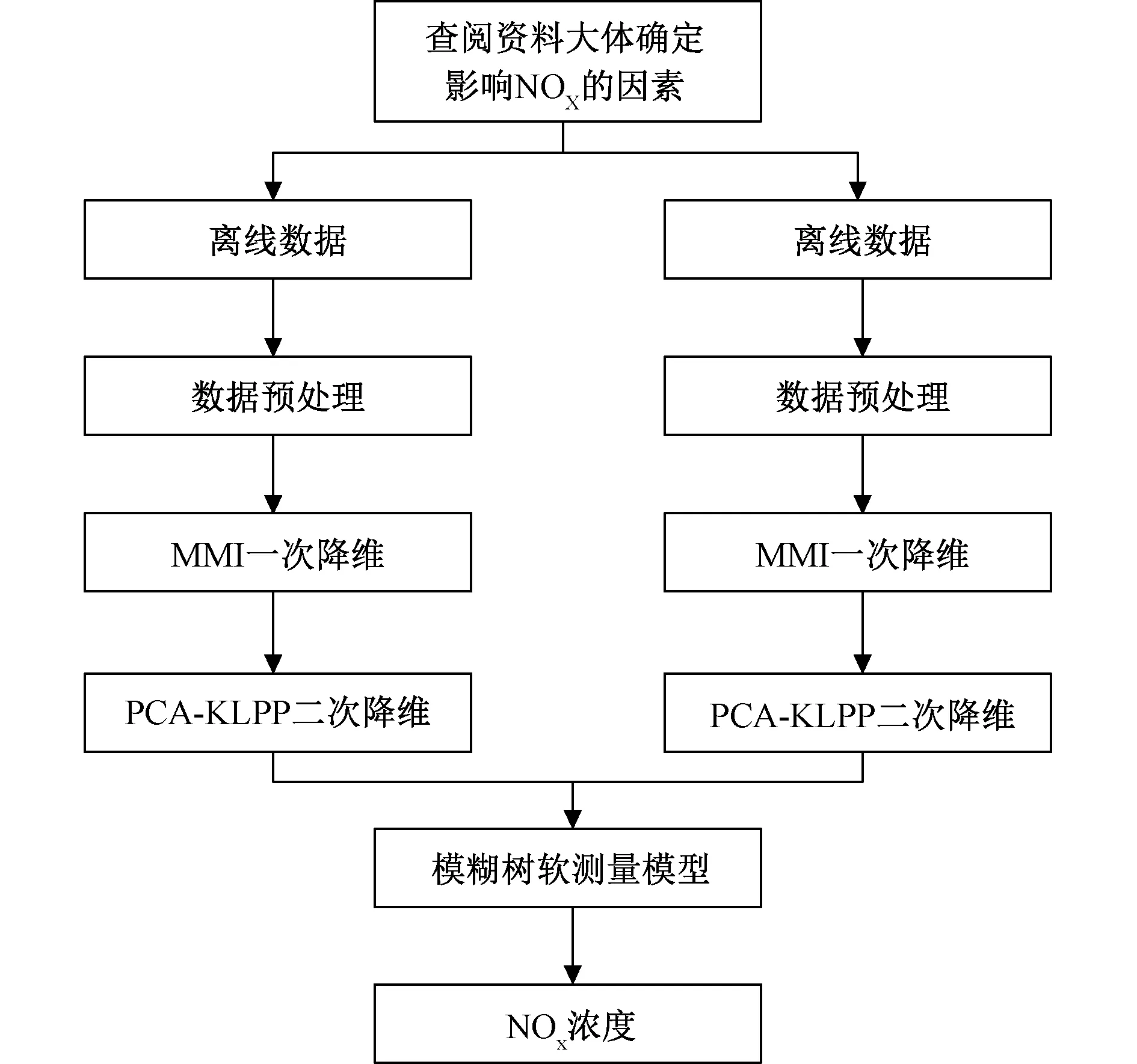
4 实验过程及结果分析
4.1 数据采集及预处理

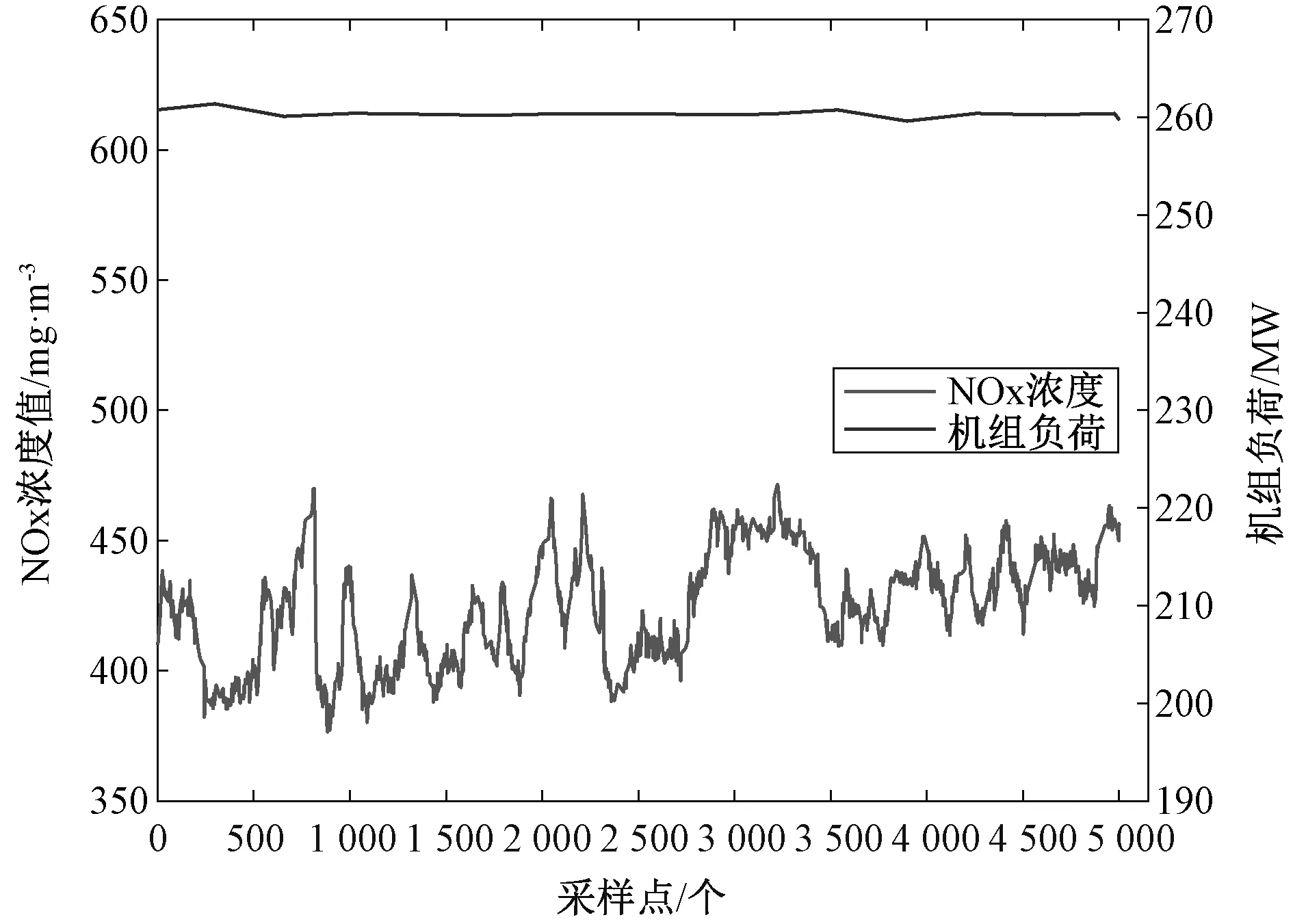
4.2 确定最佳维数

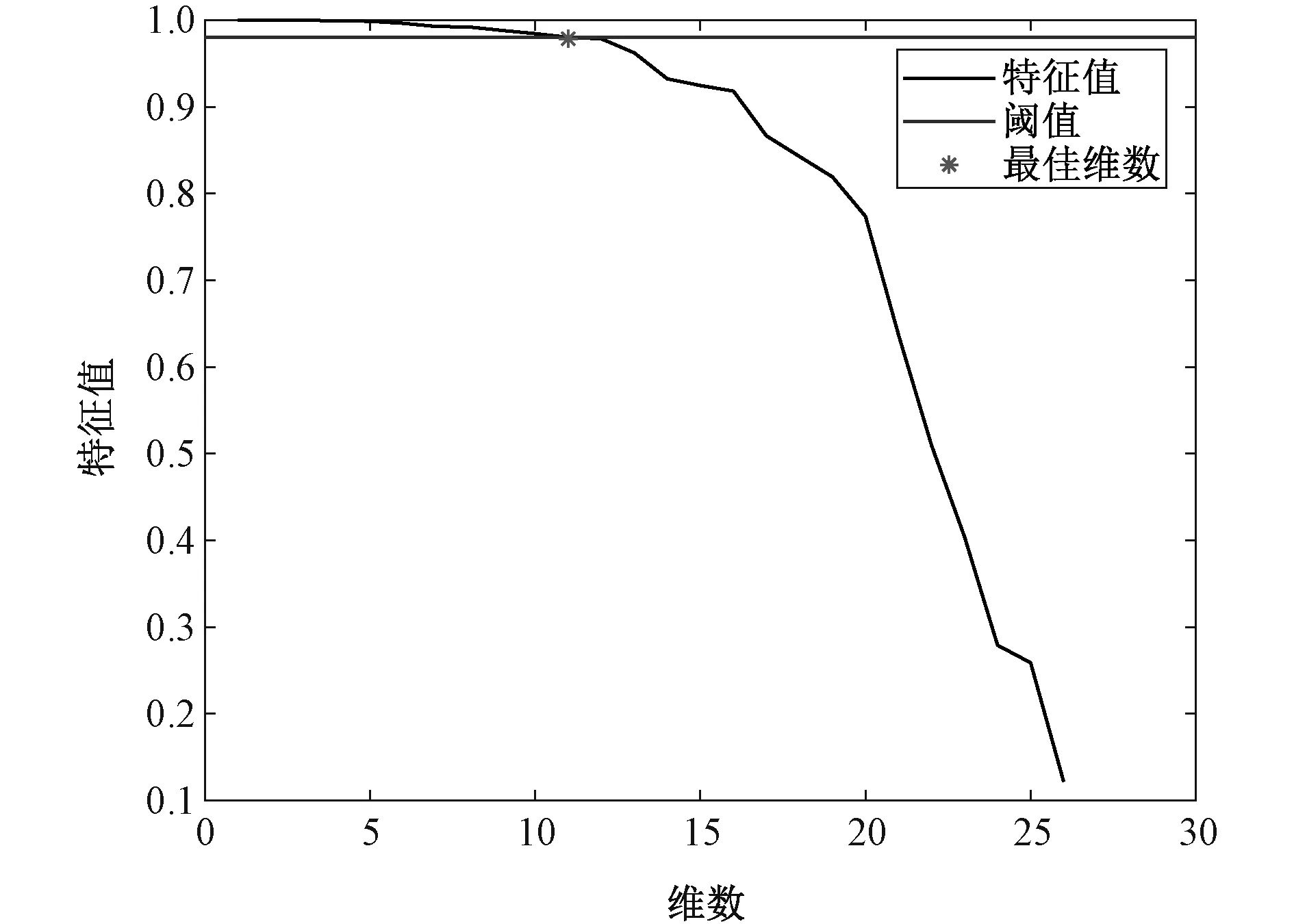
4.3 确定模糊树结构


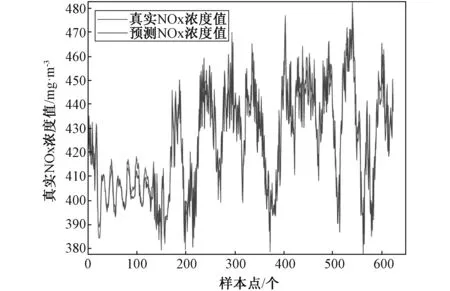

5 结 论
