适用于全桥MMC等效模型的线性排序均压算法
2020-03-11高晨祥赵禹辰赵成勇许建中
高晨祥, 赵禹辰, 常 彬, 刘 栋, 赵成勇, 许建中
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.全球能源互联网研究院有限公司,北京 102209)
0 引 言
模块化多电平换流器(Modular Multilevel Converter,MMC)凭借其开关损耗低,输出波形谐波含量少等优点,已经广泛应用于柔性直流输电工程领域中。目前,国内外在建的柔性直流输电工程大都采用MMC结构。MMC正朝着高电压大容量的方向发展,并展现出良好的发展前景[1-4]。
随着MMC电平数不断增加,非线性换流器模型的导纳矩阵阶数也将不断增加,这将使得MMC电磁暂态仿真中对非线性换流器模型的导纳矩阵求逆的计算量很大,高电平数MMC电磁暂态仿真速度极其缓慢,无法满足科研需求。为解决这一问题,国内外学者针对MMC的电磁暂态提速模型进行了深入研究[5-10],在一次系统换流阀层面和二次系统排序算法层面进行了简化与等效。目前,许多MMC的快速仿真模型在换流器部分的计算复杂度上实现了简化,文献[5]提出的MMC戴维南等效模型针对换流器进行了简化,该模型本质上是基于Dommel算法和戴维南等效原理对换流器导纳矩阵实现了降阶处理,大幅提高仿真效率,开创了MMC高精度与高效率并重的建模研究新领域。文献[6-9]提出的模型均是以戴维南等效为基础建立的,而文献[10]中提出的诸如平均值模型、开关函数模型等对换流器的简化程度较大而导致仿真精度较低。
而当换流器模型的计算复杂度降低后,排序复杂度又成为了影响仿真效率的主要因素。目前,MMC子模块电容电压排序算法主要有冒泡法、质因子分解法、希尔排序法等方法等[11-13],这些算法在实际工程和仿真分析中均适用,但这些算法的计算复杂度较高,与电平数呈非线性关系,且在用于仿真分析中时并没有与等效模型的一次系统的简化机理进行有效的结合,也即排序过程与一次系统模型完全独立,因此在仿真分析中,排序算法依然具有较大的改进空间。
文献[6]在文献[5]提出的传统戴维南等效模型的基础上将开关器件理想化并使用后退欧拉法离散化子模块电容,针对半桥和全桥子模块提出了一种理想戴维南等效模型,并基于关断电阻无穷大和后退欧拉法这两个条件提出了分组排序算法,该排序算法实现了排序算法时间复杂度与子模块个数呈线性增长,且子模块个数越多这一优势将越明显。
文献[14]和[15]中指出关断电阻若取无穷大将会丧失仿真子模块内部故障的能力,而某些情况下的故障研究需要仿真子模块内部故障[16,17],该文献理论证明了线性排序算法在关断电阻为实际值时依然适用于半桥型MMC,并且根据积分方法的不同分组的数目也有所不同,从而将该线性排序算法的应用范围拓展到了文献[5]提出的传统戴维南等效模型中去。
文献[14]和[[15]在排序算法上进行的理论拓展是基于半桥型MMC戴维南等效模型进行的理论证明与仿真验证,并没有涉及到全桥型MMC,而随着直流电网的发展,快速切除直流故障电流成为了关键性的问题,目前基于全桥型MMC的无闭锁直流故障穿越是切除直流故障的一个主流的解决方案,因此有必要分析基于全桥型MMC戴维南等效模型的线性排序算法。
本文通过理论推导,证明了在后退欧拉法或梯形积分法下,线性排序算法在关断电阻为实际值时依然适用于全桥型MMC戴维南等效模型,从而将该线性排序算法的应用范围拓展到传统的戴维南等效模型中,该排序算法与冒泡排序算法严格等效,而该证明方法可以通过简单的改变拓展到半桥型MMC戴维南等效模型的证明中去。最后,通过更具一般性的证明分析了线性排序算法的本质机理,说明了线性排序算法的分组依据并分析了该算法对于基于结构复杂子模块(一般包含不多于两个电容)的MMC戴维南等效模型的适用性。
1 全桥MMC理想线性排序算法
全桥MMC及子模块拓扑如图 1所示。

图1 模块化多电平换流器拓扑结构Fig.1 Topological structure of MMC
全桥MMC采用三相六桥臂结构,每一个桥臂都由N个子模块与桥臂电抗器Larm级联构成,每一个相单元包括上下两个桥臂。图 1中:Udc为直流侧电压;Iarm为桥臂电流;USM为子模块的输出电压;UC为子模块的电容电压;IC为子模块电容电流。
全桥型子模块电路结构如图 2 (a)所示,有正投入、负投入、旁路和闭锁4种工作状态。通过4个开关器件(T1、T2、T3和T4)开关状态的切换,子模块输出电压USM能在0和±Uc之间切换。根据单个桥臂导通子模块的数目、子模块电容电压排序结果及桥臂电流方向,选择相应的子模块触发导通,使得交流侧能够输出多电平波形。

图2 全桥型子模块示意图Fig.2 Schematic diagram of full bridge sub-module
理想情况下用可变电阻R代替IGBT/二极管开关组,且设当IGBT关断时可变电阻阻值为无穷大,采用后退欧拉法或梯形积分法离散化子模块电容,从而得到全桥型子模块的伴随电路如图 2 (b)所示。通过求取子模块戴维南等效电路并求和,可以得到单个桥臂的戴维南等效电路[6]。
当采用后退欧拉法时,在t时刻的状态相同的两个全桥子模块,在一个仿真步长内电容电压增量相等。文献[6]和[7]利用这一规律提出了一种适用于理想戴维南模型的线性排序算法。该排序算法简化了排序过程,排序复杂度与子模块个数呈线性关系。
当采用梯形积分法离散化子模块电容时,电容电压增量与两个时刻的导通状态有关,因此在桥臂输出正电平(或负电平)的状态下,子模块电容电压的增量根据两个时刻的子模块不同的通断状态分为了4种不同的值,因此排序过程将变为分4组排序,其排序复杂度为2N-3[15]。
2 全桥型MMC线性排序算法的推广证明
理想戴维南模型下,一个仿真步长内属于同一组的子模块电容电压增量相同的,所以同一组内的子模块电容电压在更新前后排列顺序不变。而实际开关器件关断电阻为一实际值(PSCAD/EMTDC中通常取1 MΩ),会导致属于同一组的子模块电容电压增量不再相等,对排序结果产生影响。下文通过理论推导,证明了同一组内的子模块电容电压在完成一个步长的更新后,排列顺序仍保持不变,即当开关器件关断电阻为实际值时,线性排序算法依然适用于全桥型MMC的传统戴维南等效模型。
根据文献[18]和[19]对于任意单端口子模块的处理方法,可将图 2 (b)的全桥子模块伴随电路转化图 3所示。

图3 全桥型子模块伴随电路Fig.3 Companion circuit of full bridge sub-module
其中GP为电容的泄露电导。
通过列写节点导纳矩阵,令G1+G2=GL,G3+G4=GS,G2G3G4+G1G3G4+G1G2G4+G1G2G3=GH,则全桥子模块的电容电压如(1)所示。
(1)
在(1)中,VCEQ(t-ΔT)=ICEQ(t-ΔT)·RC。
2.1 采用后退欧拉法时的理论证明
若采用后退欧拉法离散化子模块电容,则有:
(2)
根据式(1)和(2)可得:
(3)
假设第M个子模块和第N个子模块在同一组中,并且在t时刻VCM(t-ΔT)≥VCN(t-ΔT),则根据式(3)可以得到:
(4)
(5)
由于第M个子模块和第N个子模块在t时刻处于同一组中,因此二者通断状态相同,则式(4)和(5)中对应的电导参数均相等,对二式做差可得
VCM(t)-VCN(t)=
(6)
根据前面的假设有VCM(t-ΔT)-VCN(t-ΔT)≥0,则由式(6)可知,VCM(t)-VCN(t)≥0,即在后退欧拉法下,任意两个同组内的子模块电容电压更新前后其大小关系不发生变化。从而证明了在关断电组取实际值的时候,同一组内呈升序排列的子模块电容电压在一个仿真步长内完成更新后,依然为升序排列。排序算法示意图如图 4所示。
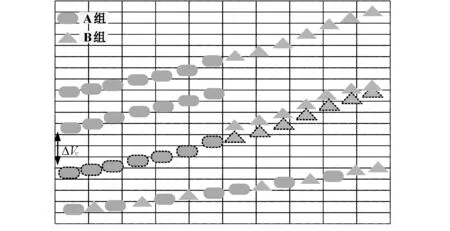
图4 线性排序算法示意图Fig.4 Schematic diagram of linear ranking algorithm
而该算法具体分组的个数的依据可以从式(3)中看出,若想求出VCM(t)-VCN(t)与VCM(t-ΔT)-VCN(t-ΔT)的符号关系,在做差时必需要消去与IARM(t)有关的项,即消去(G1G4-G2G3)项,而该项与全桥子模块的投切状态有关,因此根据全桥子模块的控制方式和投切状态,可以确定在桥臂输出正电平(或负电平)时,在后退欧拉法下,基于全桥子模块的分组排序算法应分两组进行排序,算法复杂度为N-1。
而由于半桥子模块和全桥子模块结构相近,因此该证明过程可以很显然地退化应用到半桥MMC戴维南等效模型中去,即在上述式子中令G3=0,G4→∞即可退化到半桥MMC,其子模块电容电压如(7)所示。该结果与文献[14]中结论一致。
VC(t)=
(7)
2.2 采用梯形积分法时的理论证明
若采用梯形积分法离散化子模块电容,则:
(8)
若想得到VC(t)和VC(t-ΔT)的关系,则应从式(1)和(8)入手,消去VCEQ(t-ΔT)和IC(t-ΔT)。则先求出VC(t)和IC(t)的关系。将(8)的第一行代入(1)中可得:
(9)
则VC(t)和IC(t)的关系可以求出:
(10)
通过(10)可求出VC(t-ΔT)和IC(t-ΔT)的关系,随后将(8)的第二行代入(1)中并根据VC(t-ΔT)和IC(t-ΔT)的关系,在此过程中,由于G1和G2,G3和G4之间为互补关系,因此GL,GS,GH均为常数,最终可以得到VC(t)和VC(t-ΔT)如(11)所示。
VC(t)=
(11)

同理,该证明过程亦可退化应用于半桥型MMC戴维南等效模型[14,15]。因此该线性排序的思想亦可拓展到半-全混合型MMC中去,即先对半桥和全桥子模块电容电压分别进行线性排序,再将全桥和半桥的两组结果再进行一次线性排序,可大幅提高仿真效率。
3 线性排序算法在复杂子模块构成的MMC中的适用性分析
3.1 子模块电容电压的一般性计算方法
上节证明方法是根据具体拓扑,并具体求解出全桥子模块的电容电压的解析解后进行分析的,无法分析线性排序算法是否适用于其他拓扑结构子模块MMC的仿真中。因此,本节通过更具一般性的证明分析了线性排序算法的本质机理和其适用性。
目前出现的子模块绝大多数含有不超过两个电容,因此本节的证明是基于一个新型MMC子模块结构中包含两个电容来进行的。本文中所提出的线性排序算法的证明本质上是求VC(t)和VC(t-ΔT)的关系,若该子模块的电容均连接在内部节点上,由文献[18]和[19]可知,对任一子模块来说,其电容两端节点的电压可以通过式(12)求出,
(12)
因此子模块其中一个电容的电压为VIN中两个对应的元素相减,则有:
(13)
(14)
(15)
在(15)中ICEQ1(t-ΔT)=VCEQ1(t-ΔT)·GC,ICEQ2(t-ΔT)=VCEQ2(t-ΔT)·GC,令A1-A2=A,B1-B2=B,C1-C2=C,D1-D2=D,且由于子模块电容离散化后该电路变为线性电路,可用叠加定理,则不妨设VSMEQ=K1VCEQ1(t-ΔT)+K2VCEQ2(t-ΔT),其中A、B、C、D以及K1和K2均为与子模块开关器件的等效电导有关的系数。因此,式(15)变为
(16)
3.2 复杂拓扑采用后退欧拉法时的理论分析
在后退欧拉法下,其基本公式如式(2)所示,则VC(t)和VC(t-ΔT)可以很显然的求出。对于单电容子模块来说,可以设VCEQ2(t-ΔT)=0,则很显然有:
VC(t)=(A·GC+K1·D)·VC(t-ΔT)+
(17)

对于多电容子模块来说(两个电容),可将子模块类型分为两类,一种为能够实现内部电容间自均压的子模块(如双半桥子模块[20]),另一种为不能实现内部电容间自均压的子模块(如箝位双子模块[21])。对于能够实现内部自均压的子模块来说,由于其控制方式使其内部的两个电容的电压时刻保持相等或相近,因此可认为VCEQ1(t-ΔT)=VCEQ2(t-ΔT),则该种子模块的分组方式与单电容子模块是类似的。而对于不能实现内部自均压的子模块来说,一般这类子模块的电容只起到在闭锁时箝位直流故障电流的作用,而正常运行时两个电容并没有互相充放电的回路,因此可将该类子模块结构简化为几个单电容子模块串联的情况,该种情况的分组与半-全混合拓扑的情况相似。因此,双电容子模块可根据其特性转化为单电容子模块的形式来进行证明,由此可证明,该线性排序算法对双电容子模块型MMC的等效模型也是适用的。
3.3 复杂拓扑采用梯形积分法时的理论分析
在梯形积分法下,其基本公式如式(8)所示。通过3.2的分析,对于多电容子模块可转化为单电容子模块的形式来证明,因此这里仅分析单电容子模块的情况。则式(16)可以整理为下式:
VC(t)=G·VCEQ(t-ΔT)+H·IARM(t)
(18)
其中G和H为与子模块开关器件等效电导有关的系数。则根据式(8)和(18)可得到:
(19)
可以求出IC(t-ΔT),则再根据(18)和(19)可得:
(20)
其后续的证明方式与2.2节提到的相似,即可通过证明得到在VC(t-ΔT)的系数大于0的这一判定条件下,任意两个同组内的子模块电容电压更新前后其大小关系不发生变化。要确定分组的个数,应以消去IARM(t)和IARM(t-ΔT)为出发点,可以看出,分组个数应该根据两个时刻的子模块所处的状态有关,若设子模块共有K种工作状态,那么分组的个数最多为K2个,而若采用后退欧拉法,则至多应分K组。但最终具体分组的个数仍需通过求解具体的解析解来判断。
4 仿真验证
在PSCAD/EMTDC中分别搭建了基于线性排序算法和冒泡排序算法的全桥型MMC戴维南等效模型41电平MMC-HVDC测试系统,直流电压额定值为±200 kV,子模块电容电压额定值为10 kV。本文分别设置了交流侧三相短路故障和直流侧单极接地故障以测试线性排序算法的精确度,并计算了两种模型波形的相对误差。
4.1 仿真波形对比
(1)稳态运行波形
图 5为稳态运行情况下采用不同排序算法搭建的全桥型MMC戴维南等效模型的桥臂电流电压及子模块电容电压的波形。
图中子模块电容电压波形取A相上桥臂子模块中的20个进行展示。从波形中可以看出,基于两种算法的模型的波形几乎完全重合,相对误差均在3%以内,线性排序算法有着很高的仿真精度。
(2)三相故障时运行波形
在系统运行2 s时发生三相短路故障,故障持续0.5 s。图 6为三相故障时的波形对比,并在图中标出了最大相对误差的点。

图5 稳态波形对比:(a) A相上桥臂电流,(b) A相上桥臂电压,(c)冒泡排序算法子模块电容电压,(d)线性排序算法子模块电容电压Fig.5 Steady state waveform comparison:(a) the upper bridge current of phase A, (b) the upper bridge voltage of phase A, (c) the sub-module capacitor voltage of bubble ranking algorithm, (d) the sub-module capacitor voltage of linear ranking algorithm

图6 三相短路故障波形对比:(a) A相上桥臂电流,(b)直流电流,(c)直流电压,(d) A相上桥臂电压Fig.6 Three-phase short circuit fault waveform comparison:(a) The upper bridge current of phase A, (b) DC current, (c) DC voltage, (d) the upper bridge voltage of phase A
图7为三相接地故障时采用两种不同算法的模型的子模块电容电压的波形,选取其中20个的波形进行展示。可以看出,在发生大扰动时,基于两种不同排序算法的模型的波形几乎完全重合,相对误差均在可接受范围内,表明线性排序算法在暂态故障情况下的仿真精度很高。

图7 三相短路故障时子模块电容电压:(a)冒泡排序算法子模块电容电压,(b)线性排序算法子模块电容电压Fig.7 The sub-module capacitor voltage at the state of three-phase short circuit fault:(a) the sub-module capacitor voltage of bubble ranking algorithm, (b) the sub-module capacitor voltage of linear ranking algorithm
(3)直流侧单极接地故障时运行波形
在系统运行2 s时发生单极接地故障,故障发生后3毫秒换流器闭锁,故障持续0.1 s后消失,闭锁持续1 s。图 8为故障时直流电流、直流电压、A相上桥臂电流、A相上桥臂电压的波形。图 9为直流侧单极接地故障时采用两种不同算法的模型的子模块电容电压的波形。其中子模块电容电压选取了其中20个的波形进行展示。

图8 直流侧单极接地故障波形对比:(a) 直流电流,(b)直流电压,(c) A相上桥臂电流,(d) A相上桥臂电压Fig.8 DC side pole to ground fault waveform comparison:(a) DC current, (b) DC voltage, (c) the upper bridge current of phase A, (d) the upper bridge voltage of phase A
两图中的波形证明了全桥子模块在直流故障后闭锁可以有效的隔离直流短路故障电流。可以看出,在发生单极接地故障时,基于两种不同算法的模型的波形吻合度很高,各参量相对误差均很小,基于线性排序算法的波形在直流故障以及闭锁情况下均有着很高的仿真精度。
4.2 CPU时间对比

图9 单极接地故障时子模块电容电压:(a)线性排序算法子模块电容电压,(b)冒泡排序算法子模块电容电压Fig.9 The sub-module capacitor voltage at the state of pole to ground fault:(a) the sub-module capacitor voltage of linear ranking algorithm, (b) the sub-module capacitor voltage of bubble ranking algorithm
本节分别搭建了41电平、101电平、201电平、301电平,采用线性排序算法和冒泡排序算法时的单端全桥子模块MMC系统的戴维南等效模型,并对二者的CPU用时进行了对比,计算了对应的加速比,如表 1所示。仿真总时长为1 s,仿真步长为20 μs。硬件配置为:CPU,英特尔酷睿i7-6700HQ,2.6 GHz;内存,8 GB。
从表 1中可以看出,在仿真高电平MMC时,采用线性排序算法的模型仿真用时要明显少于采用冒泡排序算法的模型,而随着电平数的进一步增加,线性排序算法的优势将更加明显。因此,在仿真由高电平数MMC构成的大规模的直流电网时,线性排序算法在仿真效率上具有很大的优势。

表 1 仿真时间对比
5 结 论
本文以快速嵌套同时求解法为基础,证明了在梯形积分法和后退欧拉法下,关断电阻为实际值时线性排序算法依然适用于全桥型MMC传统戴维南等效模型的求解。该线性排序算法的复杂度与子模块个数呈线性关系,与传统的冒泡法相比大幅提高了仿真效率,具有较强的实用性和理论创新。并且本文所提出的证明方法可以拓展到对半桥型MMC戴维南等效模型线性排序算法的证明中。
通过更具一般性的证明分析了线性排序算法的本质机理,指出了该线性排序算法分组的依据,即分组的个数与积分方法和子模块的工作状态的个数有关。在适用范围上,该线性排序算法适合用于具有相对简单结构子模块的MMC的建模仿真中,对于结构复杂的子模块来说使用该线性排序算法的仿真效率优势将不再明显。
在PSCAD/EMTDC中搭建了基于线性排序算法和冒泡排序算法的全桥型MMC戴维南等效模型,并对二者的精度和仿真效率进行了对比分析,使用线性排序算法的模型有着极高的仿真精度并且相对使用冒泡排序算法的模型提高了仿真效率,在高电平数MMC仿真时,线性排序算法有着很高的效率,因此在仿真直流电网时将具有明显优势。
