求解半线性特征值问题的搜索延拓法

谢资清

（湖南师范大学 数学与统计学院 计算与随机数学教育部重点实验室，湖南 长沙410081）

考虑如下半线性特征值问题

其中，L是一致椭圆算子，Ω⊂Rd是一个光滑有界区域，‖·‖为L2（Ω）范数，f是一个光滑非线性函数且满足f（0）=0.

模型问题（1）广泛出现在现代科学的各个领域，例如：激光传输［1］、电子结构计算［2］、玻色-爱因斯坦凝聚（BEC）［3］等.近年来，人们对模型问题（1）的一个主要研究兴趣是设计计算最小能量特征态（基态）的数值方法和建立相关理论［4-8］.随着科学技术的发展，具有更高能量的特征态（激发态）越来越受到科学家们关注.Bao 等［9］对一些用于刻画BEC的半线性薛定谔特征值问题，使用Hermite 函数构造好的初值，从数值上模拟了问题的基态和几种激发态.Chang 等［10］设计了计算BEC 能级的自适应同伦算法，能有效计算BEC 的不同能级及相应的定态解.此外，Zhou 等［11-12］将他们提出的计算非线性方程多解的局部极小极大方法推广到一类非线性特征值问题，计算了多个特征对，并建立了相关理论.

由于SEM简单、高效的优势，本文对原有SEM进行改进，使其适用于求解半线性特征值问题（1）.为此，首先在由线性算子L 的少数几个特征函数张成的子空间中逼近模型问题，得到小规模非线性代数特征值问题，求解该问题获得模型问题特征对的多个初值；然后，采用L 的更多的特征函数，进一步逼近模型问题的特征对以得到更好的初值；再用合适的数值方法离散模型问题，得到相对大规模的非线性代数方程组（非线性代数特征值问题）；最后用数值延拓法求解此非线性代数方程组，得到每个初值对应的特征对.为提高计算效率，本为将提出一种插值系数Legendre -Galerkin 谱方法用于离散模型问题（1）.

本文结构安排如下：第1 节给出求解模型问题（1）的SEM 的算法步骤和二维情形的插值系数Legendre-Galerkin谱离散格式；第2 节给出求解模型问题（1）的SEM 算法步骤和二维情形的插值系数Legendre-Galerkin 谱离散格式；第3 节应用改进的SEM 求解一类立方非线性特征值问题，给出计算实现的细节，并展示和分析数值结果.

1 求解半线性特征值问题的搜索延拓法

不失一般性，以下考虑L = -Δ的情形，则模型问题（1）的弱形式为：求（u，μ）∈（Ω）×R使其中（·，·）表示L2（Ω）内积，A（u，v）：=（▽u，▽v）.

1.1 SEM算法步骤基于原始SEM的思想，求解半线性特征值问题（1）的SEM 依次在3 层子空间Sk⊂Sn⊂SN上逼近模型问题，分为以下4 个步骤：

第一步 计算线性算子-Δ的特征对众所周知，线性特征值问题

有可数无限多特征值：

第二步 在较小的子空间Sk中逼近模型问题以获得特征对的多个初值.

定义Sk=span｛φnj：1≤j≤k｝，其中nj为互不相同的正整数.求（uk，μk）∈Sk×R使

注意到

在（3）式中，令

并取v=φni，i=1，2，…，k，得到关于k+1 个未知数（a1，…，ak，μk）的非线性代数方程组

其中a=（a1，a2，…，ak），

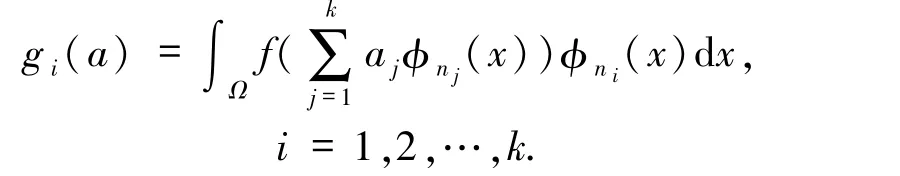
因为k较小，可通过解析方法或牛顿法等求得非线性方程组（4）的多解.特别地，当f 为多项式函数时，可利用数值代数几何方法［19］得到（4）式的所有解.显然，每组解）对应模型问题（1）的特征对的一个初值

第三步 在较大子空间Sn中进一步逼近模型问题的特征对以得到更好的初值.

为进一步逼近模型问题的特征对，取一个适当大的子空间Sn使Sk⊂Sn.设

求（un，μn）∈Sn×R使

类似于第二步的讨论，记

得到关于z=（z1，…，zn，μn）T∈Rn+1的非线性代数方程组

第四步 在大子空间SN中用合适数值方法离散模型问题并求解相应的非线性代数方程组得到最终数值解.

在SN中使用有限元、插值系数有限元或谱方法等离散模型问题（1），并用第二步或第三步得到的每个逼近解（u0，μ0）为初值，采用数值延拓法求解相应的非线性代数方程组，得到最终的数值解（uN，μN）∈SN×R.

由于第三步和第四步都涉及用数值延拓法求解非线性代数方程组，以方程组（5）为例介绍一类典型的牛顿型数值延拓法［15］.记J（z）为F（z）的雅可比矩阵.令G（z）= J（z0）（z - z0）.构造凸同伦函数

显然，H（z0，0）=0.选取适当大的正整数m 和剖分0 =t0＜t1＜t2＜…＜tm=1.考虑子问题

给定精度0 ＜ε≪ε1≪1.求解非线性代数方程组（5）的牛顿型数值延拓法的步骤如下：

1）依次对i=1，2，…，m -1，以zi，0=zi-1为初值，用如下牛顿迭代求解子问题（Pi）

zi，k+1= zi，k-（Ji，k）-1H（zi，k，ti）， k = 0，1，…，其中Ji，k=Hz′（zi，k，ti）=tiJ（zi，k）+（1 -ti）J（z0），直 到 条 件｜zi，k+1- zi，k｜ ＜ε1成 立，得 近 似 解

zi：=zi，k+1.

当｜zk+1-zk｜＜ε，得问题（5）的近似解z*：=zk+1.

1.2 插值系数Legendre-Galerkin谱离散由于谱方法具有高精度的优点，受插值系数有限元方法［1，16］的启发，本文提出一种插值系数Legendre -Galerkin谱方法用于离散半线性特征值问题（1）.下面给出二维情形的离散格式，三维和更高维情形可类似得到.

为简单起见，假设Ω =（-1，1）2.给定适当大的正整数N，考虑多项式逼近空间

其中PN为定义在I =［-1，1］上且次数不超过N的多项式的全体.令为对应于Legendre -Gauss-Lobatto（LGL）点的拉格朗日多项式基（节点基），则二维张量形式的LGL 点和相应的节点基分别为

提出如下插值系数Legendre - Galerkin 谱方法：求（uN，μN）∈SN×R使

其中IN：C（¯Ω）→PN⊗PN是基于二维LGL 点的拉格朗日插值算子，满足：

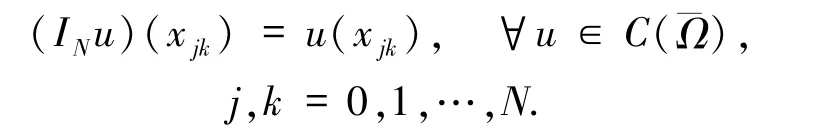
注意，（6）式中的INf（uN）是对f（uN）作整体插值.这是（6）式与标准Legendre -Galerkin 谱方法的重要区别.

注意到f（0）=0，有

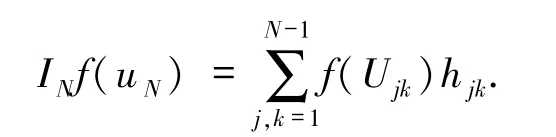
因为uN∈SN，所以

代入（6）式，并取vN=hlm，l，m =1，2，…，q =N -1，得到如下矩阵形式的非线性代数方程组

其中“∶”表示矩阵的Frobenius内积，定义为

记K=B⊗A+A⊗B，M=B⊗B，其中“⊗”表示Kronecker乘积算子，定义为则方程组（7）可重写为

容易得出F的雅可比矩阵J为

其中

由此可见，插值系数法的运用，使得雅可比矩阵的表达式（8）比标准Galerkin谱方法简单.事实上，由于K、M是常数矩阵，每步牛顿迭代中，更新雅可比矩阵的主要工作量仅是计算对角矩阵Df（¯u）.这是插值系数法的主要优点.

2 一类立方非线性特征值问题的计算

取f（u）=u3，Ω=（0，π）2，考虑半线性特征值问题

下面应用第2 节描述的SEM 求（9）式的多特征对（u，μ）.

首先，在SEM的第一步，直接计算得线性特征问题

的特征值和相应的规范正交特征函数分别为

在第二步，考虑Sk是由-Δ的对应同一特征值λ的特征函数张成的子空间.设λ 是k 重特征值，则存在k个不同的正整数对（ip，jp）∈N+×N+使得

其中a=（a1，a2，…，ak），

定理2.1非线性代数方程组（10）至少有3k-1 个解.

证明设（ip，jp）∈N+×N+满足

考虑积分

直接计算可知［15，20］：

i）若（i1，j1）=（i2，j2）=（i3，j3）=（i4，j4），Iλ=9/（4π2）；

ii）若有且仅有2 对（ip，jp）分别相等，Iλ=1/π2；

iii）其他情形，Iλ=0.于是

将（11）式代入（10）式得

设r是向量a=（a1，a2，…，ak）的非零分量个数，显然1≤r≤k.不妨假设，i =1，2，…，r，，可以得到解

下面分别对k =1，2，3，4 情形，考虑Sk由-Δ的k重特征值对应的特征函数张成，给出相应的数值结果.在数值计算中，算法第三步的Sn通常由5～20 个基函数张成.在第四步，取N =32 进行离散.数值延拓法子问题个数取为10、牛顿迭代的精度控制数取为以下特征函数的图像均在一个64 ×64 网格上呈现.

由此得到2 个（9）式的特征对数值解.图1 给出了i=1，2，3 情形得到的（9）的特征函数uii的图像，相应的特征值和初值信息列于表1.

图1 特征函数u11（左）、u22（中）及u33（右）Fig.1 Eigenfunctions u11（left），u22（middle）and u33（right）

表1 图1 所示特征函数u对应的特征值μ及初值（u0，μ0）Tab.1 Eigenvalues μ corresponding to eigenfunctions u shown in Fig.1 and their initial guesses（u0，μ0）

2）重特征情形.取

根据定理3.1，算法第二步得到32-1 =8 个特征对的初值

由此得到8 个（9）式的特征对数值解.对（i，j）=（1，2），（1，3）和（1，5），对应的几种特征函数的数值解图像绘于图2 ～4，相应的特征值和初值信息列于表2.

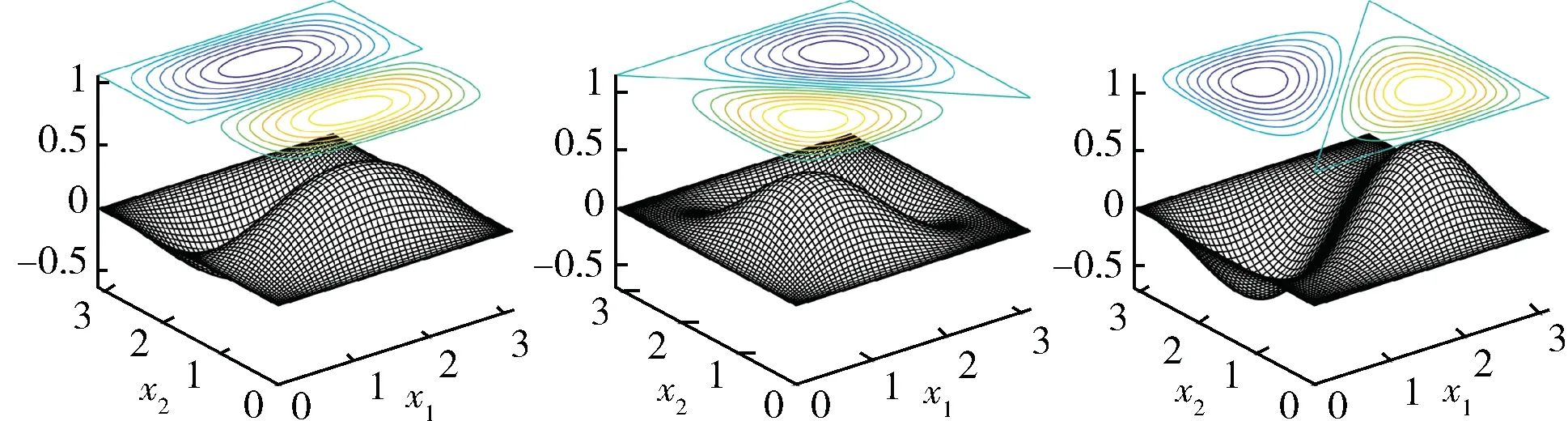
图2 特征函数u12（左）、u12+21（中）及u12-21（右）Fig.2 Eigenfunctions u12（left），u12+21（middle）and u12-21（right）

图3 特征函数u13（左）、u13+31（中）、及u13-31（右）Fig.3 Eigenfunctions u13（left），u13+31（middle）and u13-31（right）

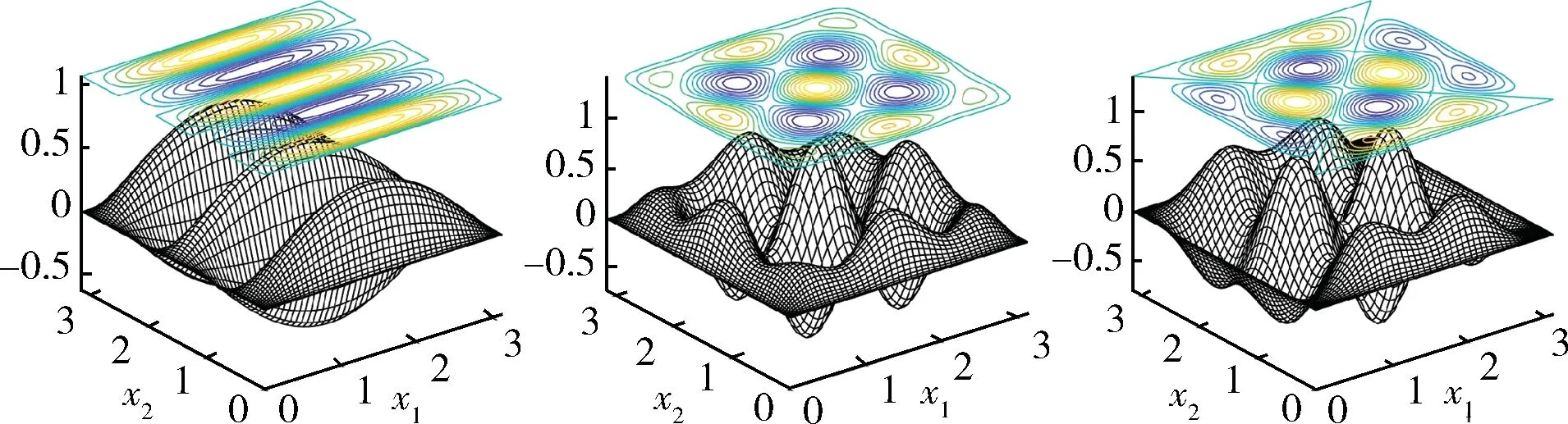
图4 特征函数u15（左）、u15+51（中）及u15-51（右）Fig.4 Eigenfunctions u15（left），u15+51（middle）and u15-51（right）

由此得到26 个（9）式的特征对数值解，其中6 种特征函数的数值解图像绘于图5 和6，相应的特征值和初值信息列于表3.

表2 图2 ～4 所示特征函数u对应的特征值μ及初值（u0，μ0）Tab.2 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.2-4 and their initial guesses（u0，μ0）

图5 特征函数u17（左）、u55（中）及u17+71（右）Fig.5 Eigenfunctions u17（left），u55（middle）and u17+71（right）

图6 特征函数u17-71（左）、u17+55+71（中）及u17-55+71（右）Fig.6 Eigenfunctions u17-71（left），u17+55+71（middle）and u17-55+71（right）

一般地，根据定理3.1，对于-Δ的任何k重特征值λ，可在算法第二步构造3k-1 个（9）式的特征对的初值.因此，理论上可以继续使用-Δ的更高重数的特征值和其对应的特征函数构造初值，并计算相应的特征对的数值解.然而，由于这时解的高度不稳定性，需要使用更大的逼近空间SN才能准确计算相应的数值解.例如最小的5 重特征值和最小的6 重特征值分别为

由于它们的值较大，本文暂未计算它们对应的解.

表3 图5 ～6 所示特征函数u对应的特征值μ及初值（u0，μ0）Tab.3 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.5-6 and their initial guesses（u0，μ0）

图7 特征函数u18（左）、u47（中）及u18+47（右）Fig.7 Eigenfunctions u18（left），u47（middle）and u18+47（right）

图8 特征函数u47+74（左）、u18+47+74（中）及u18+47+81（右）Fig.8 Eigenfunctions u47+74（left），u18+47+74（middle）and u18+47+81（right）

图9 特征函数u18+47+74+81（左）、u18-47+74+81（中）及u18-47-74+81（右）Fig.9 Eigenfunctions u18+47+74+81（left），u18-47+74+81（middle）and u18-47-74+81（right）

表4 图7 ～9 所示特征函数u对应的特征值μ及初值（u0，μ0）Tab.4 Eigenvalues μ corresponding to eigenfunctions u shown in Figs.7-9 and their initial guesses（u0，μ0）

基于上述数值结果，观测到如下现象：

若λ是-Δ的k 重特征值，相应地，半线性特征值问题（9）至少存在3k-1 个不同的特征对（若不区分同一特征值对应的正负特征函数，则问题（9）至少存在对应于λ的（3k-1）/2 个不同的特征对）.也就是说，半线性特征值问题（9）的特征对能按-Δ特征值大小排序，且密度远大于-Δ的特征对.它们的个数和分布类似树形结构，且在-Δ的多重特征值的地方派生出更多树枝.

值得一提的是，这一关于半线性特征值问题的特征对分布的数值观测，与Chen 等［15］提出并被Zhang等［20］证明的关于立方非线性椭圆方程多解分布的猜想非常类似.对上述数值观测的严格数学分析或证明还有待进一步研究.