正态总体下样本方差分布的新证法
2015-03-03常帅
常 帅
(太原师范学院 数学系,山西 太原 030031)
正态总体下样本方差分布的新证法
常 帅
(太原师范学院 数学系,山西 太原 030031)
在概率论与数理统计研究问题中,特征函数是一个重要的概念及工具.文章主要利用特征函数来证明正态总体下样本方差的分布,过程简单,易于理解.
正态分布;样本方差;特征函数;独立性
0 引言
在概率论与数理统计研究问题中,特征函数是一个重要的概念,也是一个有利的工具.特征函数完全刻画了分布函数的特征.利用特征函数,可以求一些随机变量的数字特征(如期望、方差等),也可以求独立随机变量和的分布函数,还可以求随机变量序列的极限分布,以及证明一些定理与不等式[1-2].本文将利用特征函数来证明正态总体下样本方差的分布.
1 预备知识
定义1[1-2]设X是任一随机变量,称φ(t)=E(eitX),t∈R是的特征函数.
定义2[1-2]设(X,Y)是一个二维随机变量,若E[(X-E(X))(Y-E(Y))]存在,
则称此数学期望为X与Y的协方差,记为cov(X,Y)=E[(X-E(X))(Y-E(Y))].

命题1[1-2]在二维正态分布场合下,不相关与独立等价.
命题2[2]若随机变量X与Y相互独立,又f(x),g(x)是两个连续或逐段连续的函数,则f(X),g(Y)相互独立.
命题3[1-2]设X1,X2的特征函数分别为φ1(t),φ2(t),又X1与X2相互独立,则X=X1+X2的特征函数为φ(t)=φ1(t)φ2(t).
命题4[1-2]随机变量的分布函数由其特征函数唯一决定.
命题5[3]假设X1,X2,…,Xn是独立同分布的,具有期望μ与方差σ2,


2 主要结果

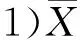
2)为了确定S2的分布,考虑



3 结论
本文利用特征函数对总体为正态分布的样本方差的分布进行推导,过程简单,易于理解.
[1] 茆诗松,程依明,濮晓龙.概率论与数理统计[M].北京:高等教育出版社,2006
[2] 魏宗舒.概率论与数理统计[M].北京:高等教育出版社,2010
[3] Sheldon M Ross.应用随机过程:概率模型导论[M].龚光鲁,译.北京:人民邮电出版社,2007
A New Proof about the Distribution of Sampling Variability from Normal Population
CHANG Shuai
(Department of Mathematics, Taiyuan Normal University, Taiyuan 030031, China)
The characteristic function is an important concept and tool for the study of probability and statistics. We prove the distribution of sampling variability from normal population using characteristic function. The process is simple, easy to understand.
normal distribution;sampling variability;characteristic function;independence
2015-07-16
常 帅(1982-),男,山西大同人,硕士,太原师范学院数学系助教,主要从事概率统计研究.
1672-2027(2015)04-0018-02
O212.1
A
