铁磁金属/绝缘体/铁磁半导体/普通金属(FM/I/FS/NM)磁性隧道结中的隧穿磁电阻效应
2020-03-07李双伶曾柏魁谢征微
李双伶, 曾柏魁, 谢征微
(四川师范大学 物理与电子工程学院,四川 成都610066)
自旋电子学[1],也称为磁电子学,是一门新兴的学科和技术.自旋电子学所涉及的领域很广,其中的一个热点是对自旋相关的隧穿磁电阻(TMR)现象的研究,近些年来该领域无论是在理论上还是在实验上都取得了很大的进展[2-3].早在1975 年,Julliere[4]就在Co/Ge/Fe这种由两层铁磁材料中间夹一薄的绝缘体材料构成的磁性隧道结中,观察到了TMR现象,得到了TMR 随铁磁电极的极化率的增大而增大的Julliere 公式.随后,Moodera 等[5]和Miyazaki等[6]利用Al2O3作为绝缘层,在三明治结构的隧道结中获得大的室温下的TMR,使磁性隧道结的研究得到了快速的发展.TMR在磁记录读写器件以及传感器等方面具有极大的应用价值,与光电传感器相比具有体积较小、可靠性较高以及功耗小等优点,因而如何提高TMR 以及得到大的自旋极化电流引起了人们的普遍关注.TMR效应的产生机理是自旋相关的隧穿效应[4,7-8],根据Julliere 公式,对于普通的铁磁金属/绝缘层/铁磁金属(FM/I/FM)三明治型磁性隧道结,由于FM 层中电子自旋极化率很有限,其TMR 的提高受到了很大的限制.另外,普通的三明治型磁性隧道结的TMR会随外加偏压的增加而迅速下降,也使得该隧道结只能在一个较低偏压下工作[9].为了克服普通三明治型隧道结中的困难,人们提出了各种各样的方案,其中的一种方法是利用电子能带对称过滤效应的Fe/MgO/Fe磁性隧道结,理论和实验上的研究结果显示该类结能得到高达200%的TMR[10-12].最近文献[13 -14]将Heusler 合金与MgO 隧道势垒结合在一起,得到的TMR 在9 K 下高达832%,在室温下达到386%.另外一种较多被人们采用的方法是利用磁性绝缘体的自旋过滤效应,如普通金属/铁磁绝缘体/铁磁绝缘体/普通金属(NM/FI/FI/NM)双自旋过滤磁性隧道结和普通金属/铁磁绝缘体/铁磁绝缘体/普通金属(FM/I/FI/NM)单自旋过滤磁性隧道结[15-16].对单双自旋过滤磁性隧道结的研究结果显示,在该类结构中不仅可以获得极大的TMR和自旋极化电流,而且能够克服普通隧道结中TMR随偏压的增高而急剧下降的缺点,但该类隧道结,由于磁性绝缘层FI厚度很小(1 ~3 nm左右),制备的难度较大.
在磁性隧道结研究的另一方面是Datta 等[17]提出了FM/S/FM(S表示半导体)结构的场效应晶体管,已有的研究结果表明,随着S 层中Rashba 自旋轨道耦合强度的变化,其隧穿磁电阻呈现周期性的振荡[18-23].由于可以通过电场来控制Rashba 自旋轨道耦合效应,实现一种全电学的控制方法,因而半导体中的Rashba 自旋轨道耦合效应在磁性隧道结中的研究和应用引起了人们极大的关注[19-23].
对于FM/I/FI/NM自旋过滤隧道结,其TMR将随FI层厚度的增加而下降,这样要得到大的TMR值,FI层必须很薄,因而带来了制备上的困难.本文在前人所研究的基础上,将FM/I/FI/NM中的FI层用铁磁半导体FS 层代替,研究了FM/I/FS/NM 中TMR随Rashba自旋轨道耦合强度、势垒高度、分子场、及各中间层厚度的变化.相应的计算结果对自旋过滤效应和Rashba 自旋轨道耦合效应在自旋电子器件中的研究和应用具有一定的参考价值.
1 FM/I/FS/NM隧道结的理论模型

图1 为FM/I/FS/NM隧道结的结构示意图,其中自旋量子化轴取为z轴方向,θ为FM层和FS 层中分子场夹角,FM 为铁磁金属,I 为绝缘体,FS 为铁磁半导体,NM 为普通金属.由于在零偏压条件下,对隧穿起主要影响的是垂直入射的电子(沿x轴方向),同时由于横向限制,可假设隧道结具有准一维结构,其各层的Hamilton[21-26]为

图1 FM/I/FS/NM隧道结构示意图Fig.1 The schematic of FM/I/FS/NM tunnelling junction

其中hFM、hFS代表铁磁金属层和铁磁半导体层中分子场大小.
由(1)式,将各层中的波函数表示为


在以上各式中mFM、mFS分别表示FM、FS 材料层中的电子有效质量,h为普朗克常数,kR2为FS层材料中的Rashba自旋轨道耦合效应强度.分别表示上自旋电子和下自旋电子,而均为待定系数.
根据各层界面处波函数连续和一阶导数连续关系,以及旋量变化关系列出如下方程:
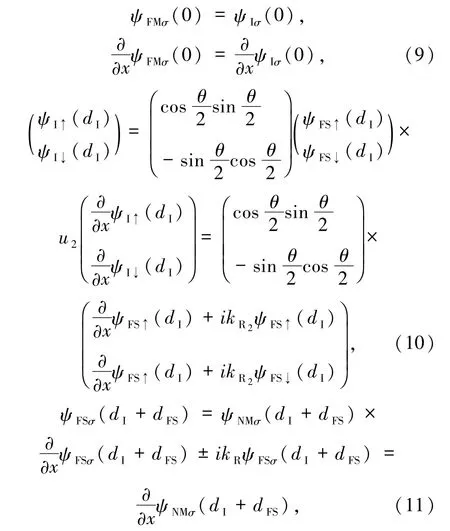
根据Laudauer-Büttiker方程[27],隧穿电导为

其中Tσ(θ)为自旋电子的透射率,TMR 的表达式[7]可写为

由方程(9)和(10)可解得待定系数,从而得到隧穿系数,再由方程(12)和(13)得到隧穿电导和隧穿磁电阻TMR.
2 计算结果讨论
在以下对FM/I/FS/NM 隧道结中电子的隧穿输运特性的计算讨论中,设为自由电子的质量,铁磁半导体FS 中的分子场大小,费米能E =2.47 eV[22],各层能带差
2.1 FM/I/FS/NM 隧道结的TMR 随FS 层厚度以及I层厚度的变化在TMR与FS 层厚度dFS的关系计算中,分别取kR2等于1k0、3k0、5k0,非磁绝缘I层厚度,I层势垒高度计算结果如图2 所示,图2(a)~(c)是FM/I/FS/NM结的计算结果,从中可以看出,在不同的kR2值下,TMR值随FS层厚度的变化而振荡,其振荡曲线的振幅变化呈周期性的趋势.这样对应于FS 层厚度变化,存在一个周期性的区域,在该区域内可获得很大的TMR值.图2(d)是对FM/I/FI/NM 结计算的结果,结果显示FM/I/FI/NM 中的TMR 随FI 层厚度增加下降的很快.图2 中分子场hFM为1.92 eV,hFS和hFI为0.18 eV,绝缘层I 的厚度为1 nm,势垒高度为3.0 eV.由此可见,FM/I/FS/NM 结可以在FS层厚度dFS很大的情况下得到极大的TMR值并可以根据需要选择FM/I/FS/NM结中FS层的厚度,从而避免了自旋过滤磁性隧道结由于磁性势垒层厚度很小而带来的制备方面的困难.
图3 为FM/I/FS/NM结的TMR值在不同自旋轨道耦合强度kR2下随绝缘层厚度dI的变化.计算中取FS层厚度为410 nm(由前面计算结果可知FS层厚度为410 nm时,可以获得460%大的TMR值)其它参数如势垒高度、分子场大小等和图2 一样.从图3 可以看出,当dI小于0.5 nm时,随着dI的增加,TMR值迅速增大,当dI增大到1 nm后,TMR值趋于稳定达到饱和状态.这说明FM/I/FS/NM结中的绝缘层的厚度dI适中即可.
2.2 FM/I/FS/NM 结构中TMR 随铁磁半导体层分子场大小的变化当保持各层厚度和势垒高度不变,对应于FS层中不同的自旋轨道耦合强度,TMR与FS层的分子场大小关系计算结果如图4 所示,计算中势垒高度取为3.0 eV,I 的厚度dI为1 nm,FS 厚度为410 nm,FM 层中的分子场hFM为1.92 eV.从计算结果可看出TMR 随分子场hFS的变化并不是单调增加,并且随kR2的增大,TMR 对应的第一个峰值往后移动.

图2 图(a)~(c)为FM/I/FS/NM隧道结的TMR随铁磁半导体厚度dFS变化;(d)图为FM/I/FI/NM隧道结的TMR随FI层厚度的变化Fig.2 (a)-(c)are the variations of TMR with the thicknesses of the ferromagnetic semiconductor layers in FM/I/FS/NM structures;(d)is the variations of TMR with the FI layer thickness in the FM/I/FI/NM structures

图3 FM/I/FS/NM隧道结中,TMR随绝缘层(I)厚度dI 的变化Fig.3 In the FM/I/FS/NM junctions,the varitations of TMR with dI the thicknesses of the insulator I layer
2.3 FM/I/FS/NM结构中TMR 随Rashba 自旋轨道耦合强度的变化在TMR 值与Rashba 自旋轨道耦合强度的关系计算中,取I 层厚度为1 nm,FS层厚度为410 nm,其他参数保持不变,计算结果如图5 所示.从图5 的计算结果中可以看出,TMR随kR2的增大出现明显的振荡现象.另外,随着kR2的增大,振荡曲线的波峰和波谷都变得越来越尖锐,整个曲线的包络出现周期性变化的趋势.从图5中还可以看到,TMR 值随kR2的变化曲线并不随θ的变化而移动,说明曲线的振荡周期不随FS 层与FM层磁矩的相对夹角的变化而变化.

图4 FM/I/FS/NM隧道结中,TMR随FS层中分子场hFS的变化Fig.4 In the FM/I/FS/NM junctions,the variations of TMR with the hFS in the FS layer
2.4 FM/I/FS/NM 结构中TMR 随绝缘层势垒高度的变化当取绝缘层为1 nm,铁磁半导体层厚度为410 nm,TMR 值和势垒高度的数值计算关系如图6,从该结果看出当势垒高度在0 ~5 eV 范围内变化时,TMR 出现振荡现象,当势垒高度大于5 eV后,TMR 则略趋于稳定,不再振荡.所以在实际情况中可以取合适的绝缘层势垒高度来得到较大或稳定的TMR值.

图5 FM/I/FS/NM隧道结中,对应于不同的θ值,TMR随kR 2的变化Fig.5 In the FM/I/FS/NM junctions,the variations of TMR with kR 2 for different θ
3 结论
本文计算了自旋过滤隧道结FM/I/FS/NM 中TMR和各层厚度、势垒高度以及Rashba 自旋轨道耦合强度的关系.研究结果表明由于FS层中Rashba自旋轨道耦合效应的影响,FM/I/FS/NM结构中TMR随FS 层厚度的增加呈振荡变化,随绝缘层I的厚度变化呈饱和状态,因而可以适当选取FS 层和I层厚度来得到极大的TMR值.和已有的FM/I/SF/NM单自旋过滤隧道结相比,由于FS 层厚度可以做的较大,这样可以克服FM/I/SF/NM单自旋过滤隧道结中TMR随铁磁绝缘层厚度增加而下降的缺点.本文的这些研究结果可对磁性隧道结中的自旋相关电子隧穿输运特性及其与Rashba 自旋轨道耦合的关系的理解提供一定的帮助,对相关的自旋电子器件的设计与应用也具有一定的参考价值.

图6 FM/I/FS/NM隧道结中,TMR随绝缘层势垒高度UI 的变化Fig.6 In the FM/I/FS/NM junctions,the TMR changes with the insulator barrier height UI
