不确定数据流上的离群点检测处理
2020-03-02朱斌钟毓灵王习特白梅
朱斌,钟毓灵,王习特,白梅
(大连海事大学 信息科学技术学院,辽宁大连116026)
离群点检测是数据管理领域的热点问题之一[1],广泛应用于工业损毁、金融诈骗和环境监测等应用场景中,离群点被认为是数据集合中显著区分于其他数据点的数据对象[2].目前,因为基于距离的离群点定义[3]能够直观反映离群点本质而得到广泛的应用,其具体描述为:对于数据集合中任意数据点p,若p在半径r范围内的邻居个数少于k个,那么p被认为是离群点.
近年来,数据以高速度高容量的流式形式应用于工业生产、社会生活中,在这规模庞大、速度极快的流式数据里面,不确定性数据广泛存在于其中[4].数据的不确定性主要分为属性级不确定与存在级不确定,本文主要关注存在级不确定数据[5].目前,传统的离群点检测算法尚无法满足诸多现实需求,以气象监测系统为例,传感器不间断地采集局部气温、气压和紫外线指数等环境信息并以流的形式传输到数据库中,实时识别出离群点(异常气象信息),可以有效地防范自然灾害.但是,受到传感器精度及周围环境等因素影响,产生的数据流具有流速较快、规模较大及不确定性等数据特点,使得传统解决方案无法直接应用到上述问题中[5].因此,设计出一种高效的不确定数据流上的离群点检测算法成为本文的主要研究目标.
文献[6]首次给出了存在级不确定数据中的离群点定义,并提出了DPA算法用以解决集中式环境中的离群点检测问题.随后,文献[7]在文献[6]的基础上将研究内容扩展至不确定数据流环境中,利用网格索引结构管理不确定数据,并采用动态规划思想来求解离群概率值用以避免可能世界的空间膨胀.但因该算法在批量过滤时不可避免地需要近邻空间的查询,这就使得在处理多维数据时具有一定的局限性,另外,由于其忽略了离群概率值求解的递推规律,使其在概率值求解中也无法避免冗余计算.文献[8]也关注于该研究问题并提出了PCUOD算法,该算法通过估算数据点的离群概率范围进行概率剪枝,从而减少了必要的计算成本.但是,由于PCUOD算法中的界限估算方法在近邻数目急剧增加时会产生失效的情况,从而也造成了一定的局限性.总之,目前相关解决方案中仍存在诸多不足,无法高效地满足现实应用的需求.
本文主要研究快速不确定数据流上的离群点检测算法(Fast Outlier Detection algorithm Over Uncertain Data Streams,FOD_OUDS),旨在提高算法的执行效率.主要贡献包括以下几个部分:
1)采用分层次划分思想给出了不确定数据流环境中索引的构建方法,利用这种索引结构可以克服传统索引对多维数据管理的局限性.与此同时,本文通过对索引结构中的叶子子块增加部分存储信息,可以快速地完成新到达数据点的批量过滤,极大地减少了数据更新过程中的计算代价.
2)通过深入分析离群概率值求解的递推规律后,提出了一种新的离群概率值求解方法.该方法尽最大可能地避免了全近邻集合的迭代计算,从而极大地减少了冗余计算.
3)利用大量的对比实验,验证本文所提出的FOD_OUDS算法的有效性.
1 不确定数据流离群点检测算法
1.1 问题描述
本文主要研究不确定数据流环境中基于距离的离群点检测问题.首先,给出不确定数据流中基于距离的离群点定义;然后,简要描述在基于计数的滑动窗口上的处理流程.表1列出了本文使用的符号及其含义.
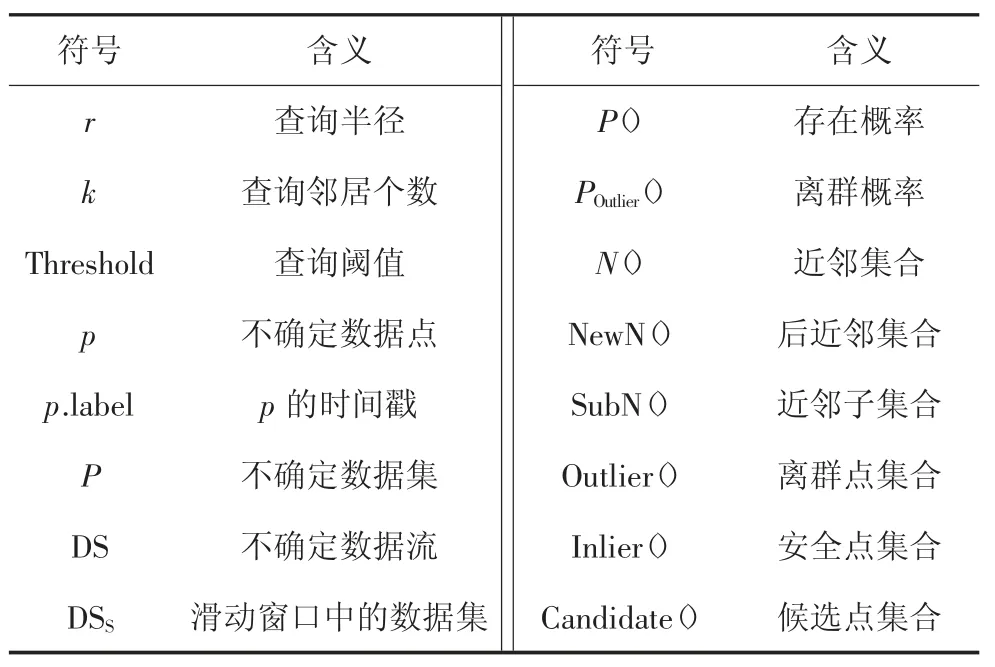
表1 符号列表Tab.1 List of symbols
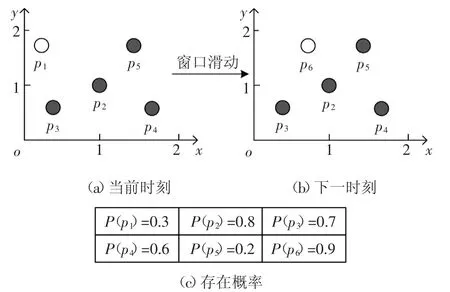
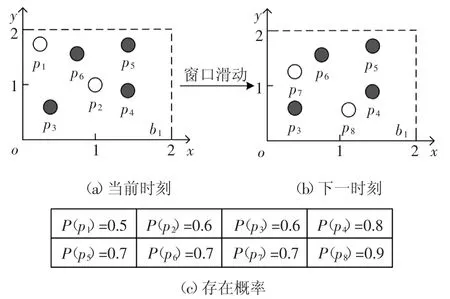
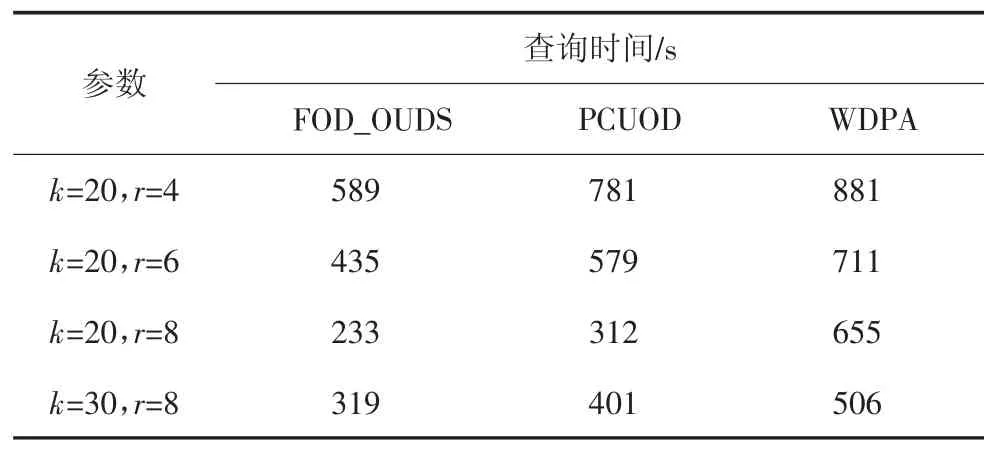
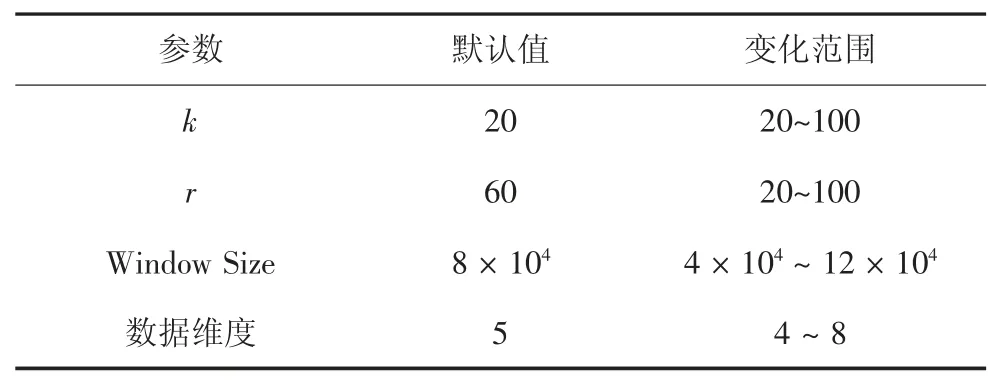
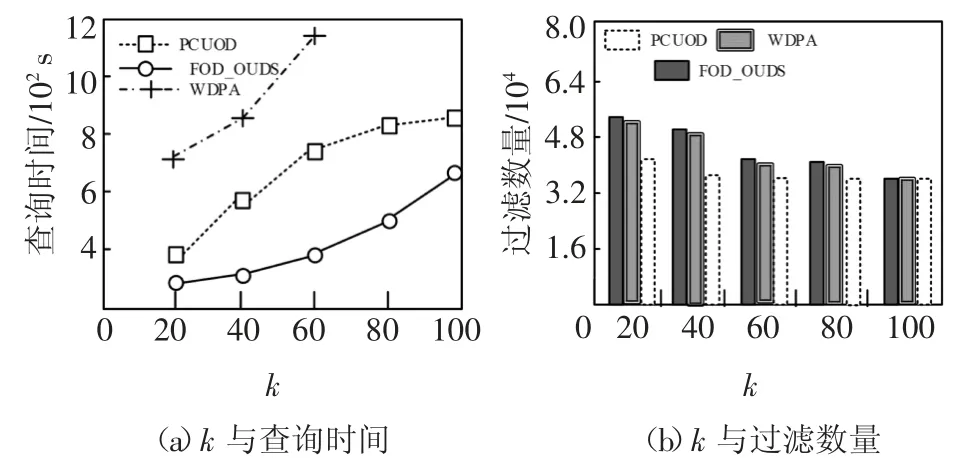
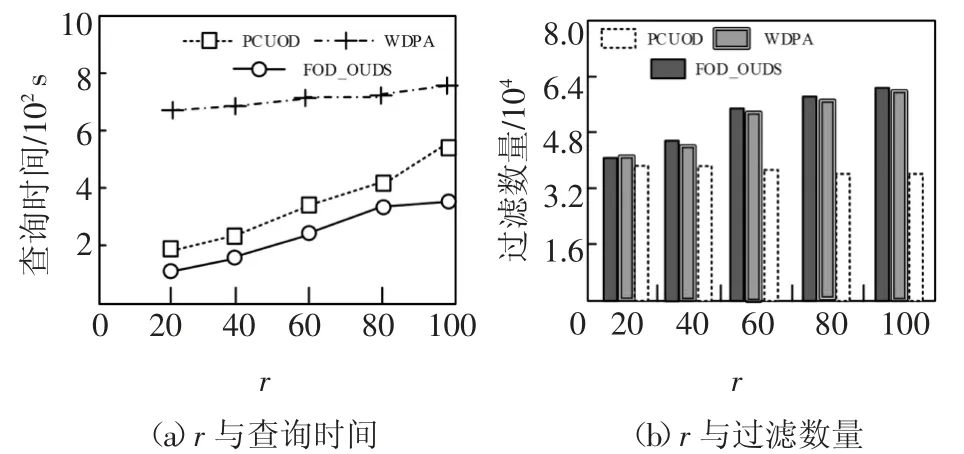
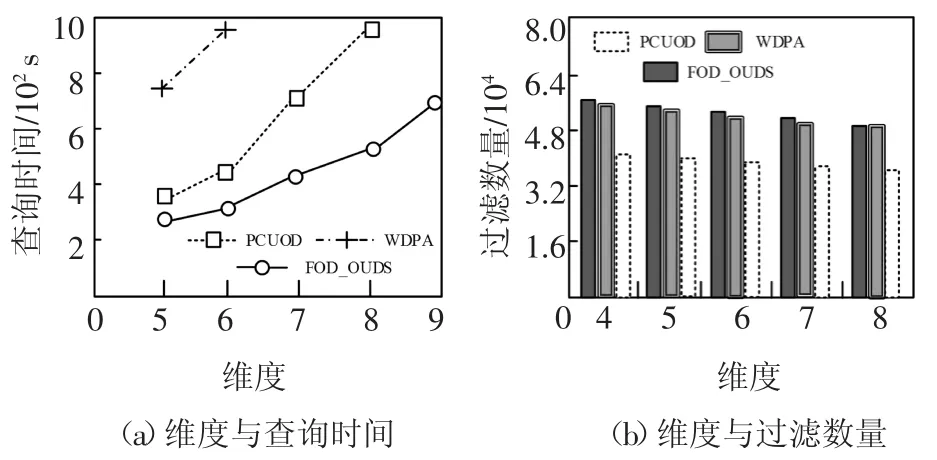
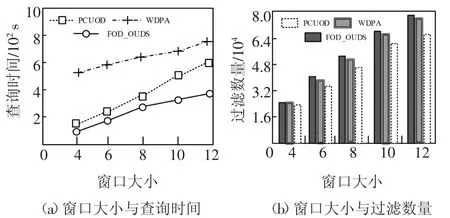
DS表示具有d维属性的不确定数据流,在DS中任意数据点p都有一个存在概率P(p)(0 定义1(r-近邻)给定数据集P和查询半径r,点p在P内的近邻集合是p在r范围内包含的所有点的集合,即N(P,p)={p′|p′∈P,dist(p,p′)<r}. 定义2((r,k)-离群点)给定数据集P和查询邻居个数k,若点p是P内的(r,k)-离群点,则p在半径r范围内的邻居个数小于k,即 在数据集P中每个可能世界W都是P的子集.W的存在概率为: 定义3(Threshold-离群点)给定查询阈值Threshold,若点p的离群概率POutlier(p)>Threshold,那么p是Threshold-离群点. 可知,所有满足定义3的点组成了数据集P中的离群集合Outlier(P)={p|p∈P,POutlier(p)>Threshold}. 在不确定数据流DS上,采用基于计数的滑动窗口模型管理数据,严格按照数据点p到达窗口的先后次序标记p的时间戳p.label.当窗口大小是S时,窗口内的数据集记作DSS,窗口内的点的生存周期是[p.label,p.label+S].同时,窗口中保存且仅保存最近到达的S个数据点,因此每当窗口中扩充一个新的点pnew时将对应一个旧的点pold消失. 具体描述为,滑动窗口中的不确定离群点查询就是返回当前窗口中所有离群概率大于阈值的数据点的集合,就是Outlier(DSS)={p|p∈DSS,POutlier(p)>Threshold}. 例1图1(a)(b)分别给出了当前时刻与下一时刻滑动窗口内的数据点集,图1(c)给出了每个点的存在概率.假设窗口大小S=5,查询半径r=3,查询邻居个数k=3和查询阈值Threshold=0.6,数据点按照p1~p6的次序到达.以点p2为例,根据上述定义,当前时刻p2的离群概率POutlier(p2)≈0.63,可知p2是离群点.下一时刻,随着窗口的滑动点p6到达而点p1消失,p2的离群概率变为POutlier(p2)≈0.42,可知,随着窗口的滑动,下一时刻p2将变为非离群点. 图1 处理流程示例Fig.1 The example of process flow 首先,采用分层次划分索引结构管理不确定流数据;然后,提出了全新的过滤方法;最后,给出了离群点查询动态维护的更新方法. 1.2.1 索引模型 采用分层次划分索引结构管理不确定流数据.这种索引结构:一方面,可以克服传统索引对多维数据管理的局限性;另一方面,能够避免过多空白子块的产生,减少了存储空间的浪费.同时,利用划分子块内不确定数据点的特性,可以快速批量过滤数据点,从而加速最终结果的查询. 在文献[9]工作的基础上,采用相同的划分策略构建索引结构.为便于后续批量过滤,将每个划分子块b内的数据点按照存在概率由大到小的顺序排序,并记录块内数据点个数b.num和块内空间最大距离b.dis. 1.2.2 过滤方法 首先,给出了空间数据点的批量过滤方法,利用这种方法可以在遍历划分子块的过程中,通过快速估算出子块内数据点整体的离群概率上界限值来完成批量过滤操作;然后,提出了一种新的离群概率值计算方法用以减少离群概率值的计算代价,该方法尽最大可能地避免了全近邻集合的迭代运算,从而减少了大量的运算成本,提高了算法的运算效率. 批量过滤方法具体的理论依据由引理1给出. 引理1[9]给定查询半径r.在b.dis<r的划分子块b中,若点p1的存在概率小于点p2的存在概率,那么在b中p1的离群概率一定小于p2的离群概率. 批量过滤时,利用引理1,按照存在概率值由大到小的顺序计算出数据点在划分子块b内的离群概率,若某一数据点的离群概率小于Threshold,那么在子块b中存在概率不大于该点的点均为非离群点,由此可以完成划分子块b中数据点的批量过滤操作. 离群概率值计算方法通过深入分析离群概率值求解的递推规律后给出了一种新的解决方案,该方案可以最大可能地避免全近邻集合的迭代计算从而减少运算成本的消耗.具体的理论依据由定理1给出. 定理1给定不确定数据点p和点p的近邻集合N(p),如果n_MaxSubN(p)是近邻集合N(p)中存在概率最大的n个近邻点组成的子集合,那么在所有由N(p)中n个近邻点组成的子集合里,点p在子集合n_MaxSubN(p)中成为离群点的概率值最小. 证明:给出查询邻居个数k,不确定数据点p和点p的近邻集合N(p).其中,n_SubN(p)是由近邻集合N(p)中n个点组成的近邻子集合. 当n<k时,点p在近邻子集合n_SubN(p)中成为离群点的概率值等于点p自身的存在概率值,即POutlier(p,n_SubN(p))=P(p). 易知,当n=k时,若n_SubN(p)是由N(p)中存在概率最大的k个点组成的子集合,则点p在子集合n_SubN(p)中成为离群点的概率值最小. 当n>k时,假设点p在由N(p)中存在概率最大的n个点组成的子集合n_MaxSubN(p)中成为离群点的概率值最小.那么当n_MaxSubN(p)中扩充一个数据点p′(p′∈N(p)∧p′∉n_MaxSubN(p))时,点p在新的近邻子集合中成为离群点的概率值为: 其中:P(a-n_MaxSubN(p))是子集合n_MaxSubN(p)中a个数据点发生的概率.由此可见,不确定数据点p′的存在概率越大,点p在新扩充的子集合中成为离群点的概率值越小.综上,可证明结论成立. 证毕. 由定理1可知,在求解数据点p的离群概率值时,按照近邻集合中近邻点存在概率值由大到小顺序来计算,可以保证每一次的计算中点p在当前近邻集合中成为离群点的概率值都是最小的.那么,为了快速判定点p是否为非离群点,进一步给出引理2. 引理2[9]给定数据点p和p的近邻集合N(p),p的离群概率随着N(p)中点的个数的增加而减少. 由引理2可知,若数据点p在其近邻子集合中成为离群点的概率值小于查询阈值,那么点p将是一个非离群点.也由此可知,根据定理1按照近邻集合中近邻点存在概率值由大到小的顺序来求解点p的离群概率值,若点p是非离群点则可以在最少的迭代计算中判定出来.具体示例由例2所示. 例2图2展示了b1.dis 图2 批量过滤示例Fig.2 The example of batch filtering 1.2.3 更新方法 为节省窗口滑动时数据更新所带来的计算成本,本小节中首先分析了不确定数据流中离群点的性质,并将滑动窗口内的数据进行归类,用以避免对部分数据点的重复计算.然后,对当前窗口中的叶子划分子块增加了部分存储信息,使得新到达窗口中的数据点可以利用存储信息直接完成批量过滤,从而达到减少计算成本的目的. 首先,给出定理2用以确定窗口中不可能成为离群点的数据点,以此避免重复计算. 定理2给定不确定数据点p,若点p在后近邻集合NewN(p)中的离群概率值小于查询阈值,那么点p不可能成为离群点. 证明根据引理2可知,若点p在近邻子集合中的离群概率值小于查询阈值,那么点p的离群概率值一定小于查询阈值.又因为NewN(p)中的近邻点到达窗口都比点p晚,所以若点p在后近邻集合NewN(p)中的离群概率值小于查询阈值,则点p将不可能成为离群点. 证毕. 由此更新维护时,对于满足定理2的点将永远不可能成为离群点,也就不需要被更新计算. 具体地,可将当前窗口内的数据DSS分为以下3类集合:1)当前窗口内的离群点的集合Outlier(DSS).2)当前窗口内是非离群点但随着窗口滑动可能成为离群点的候选集合Candidate(DSS).3)所有满足定理2的安全点的集合Inlier(DSS). 然后,对当前窗口中的叶子子块增加部分存储信息并利用这些存储信息来直接完成新到达数据点的批量过滤.与此同时,给出了划分子块中批量过滤的动态维护过程. 对于叶子划分子块将增加部分存储信息,包括3个部分:1)记录b内是非离群点且存在概率最大的点p的存在概率b.temp;2)记录包括点p和点p按照定理1满足它在b中的近邻子集合中是非离群点的近邻子集合的集合b.SubN;3)b.SubN中最早消失的数据点的时间戳b.label. 下面,主要介绍批量过滤的动态维护,包括处理失效数据点pold和处理新插入数据点pnew. 1)失效数据点pold的处理.对于pold映射到的划分子块b,若pold属于b.SubN,则需要更新b的记录信息并更新b中的批量过滤.若pold不属于b.SubN,则直接删除pold. 2)新插入数据点pnew的处理.检测pnew映射到的划分子块b,如果P(pnew)<b.temp那么pnew是非离群点并加入到候选集;如果b.temp<P(pnew),那么需要更新b的记录信息并更新b中的批量过滤,用以过滤更多数据点. 例3展示了利用划分子块的存储信息完成新到达数据点的批量过滤并给出了动态维护的过程. 例3图2(a)(b)分别展示了当前时刻与下一时刻划分子块b1内的数据点集.假设r=3,k=3和Threshold=0.6.当前时刻b1的记录信息b.label=2、b.temp=0.8和b.SubN={p4,p5,p6,p2}.根据引理1,b1内的点均为非离群点,其中,p1是安全点,其他点是候选点.下一时刻,b1中点p6和p7到达而点p1和p2消失.首先处理消失点:当p1消失时,不会影响b1中的过滤;当p2消失时将重新计算b1中的记录信息,有b.label=3、b.temp=0.8和b.SubN={p4,p5,p6,p3},此时b1中各点均为候选点.然后处理新插入点:当插入p7时,因P(p7)<b.temp可直接判定p7是候选点;当插入p8时,因b.temp<P(p8)需要更新b1的记录信息,经计算b.label=6、b.temp=0.9和b.SubN={p8,p7,p6}.此时,b1中各点均是非离群点,其中p8、p7和p6是候选点而其他点是安全点. FOD_OUDS算法描述:输入:滑动窗口数据集DNS,查询阈值Threshold,查询邻居个数k,查询半径r,待删除点pold,待插入点pnew;输出:离群集合Outlier(DNS)1.WHILE pnew插入到当前窗口中DO 2.IF滑动窗口已满DO //处理失效点pold 3.删除待消失数据点pold;4.IF pold在b记录的集合b.SubN中THEN 5.更新b的记录信息,并更新b中的批量过滤;6.ENDIF 7.集合D←近邻集合N(pold)中未被处理更新的点;8.FOR遍历集合D中的数据点p DO 9.计算属于候选集中的点p的离群概率,如果p的离群概率大于阈值,那么将p移入到离群集中.10.ENDFOR 11.ENDIF//处理插入点pnew 12.根据P(pnew)将其插入到所映射的划分子块b中;13.IF P(pnew)大于b的b.temp THEN 14.更新b的记录信息,并更新b中的批量过滤;15.ENDIF 16.集合D←近邻集合N(pnew)中未被处理更新的点;17.FOR遍历集合D中的数据点p DO 18.计算属于候选集或离群集中的点p的离群概率,若p的离群概率小于阈值,根据定理2,将其加入到候选集或安全集中;19.ENDFOR 20.IF pnew未被b中过滤THEN 21.计算pnew的离群概率,若pnew的离群概率小于阈值,则将pnew加入到候选集,否则加入到离群集;22.ENDIF 23.ENDWHILE 在检测过程中,首先,判断当前滑动窗口内数据是否已满,若是,则每当有新的点pnew到达窗口时都将对应一个旧的点pold失效(算法中行2),并考虑删除pold后对它近邻点和对它映射到划分子块的批量过滤的影响,其近邻集合中的某个原来属于候选集的点,有可能变为离群点(算法中行3~行11).然后,对于新插入的点pnew,一方面需要考虑pnew的到达对它近邻点和它映射到划分子块的批量过滤的影响,并做出相应的调整.另一方面,检测pnew是否能被批量过滤,若不能则计算它的最终结果(算法中行12~22). 实验采用C++编程语言实现不确定数据流上的离群点检测算法.环境配置为Inter Core i5 3230 2.6 GHz CPU,6 GB内存,Winsows10操作系统. 在对比实验中,对本文提出的FOD_OUDS算法与WDPA(Dynamic Programming Algorithm for Window)算法[7]和PCUOD(Probability Pruning for Continuous Uncertain Outlier Detection)算法[8]分别在真实数据集和人工模拟数据集中进行性能对比.其中,真实数据集采用的是森林环境监测数据,共包含120 000个数据点和4个属性维度,其中,每一个属性值均被映射在0~100范围内.由于真实数据并非是概率数据,所以对每一个数据点随机生成一个存在概率值来增加概率属性.实验中主要对比的是查询时间,表2展示了对比实验的实验结果. 表2 实验结果Tab.2 Experimental result 表2展示了真实数据集中3种算法的性能对比,其中,由于WDPA算法采用网格索引结构管理不确定数据并在批量过滤时不可避免地需要近邻空间查询,因而在4维数据中的检测代价相对较高.而对于PCUOD算法,由于其在近邻数目较多时过滤性能将会减弱,因而过滤性能相对较低,从而导致需要精确计算的数据点增多使得查询较为缓慢.相比之下,由于FOD_OUDS算法采用分层次划分索引,因而能够较好地管理多维数据,并且在过滤方法中避免了近邻空间的查询,也最大可能地避免了全近邻集合迭代计算,因而拥有较好的处理性能. 在人工模拟数据集的对比实验中,默认的测试数据具有5个维度属性,每个维度属性值被映射到0~1 000内,并对每个数据点随机生成一个存在概率值.实验中主要考察查询邻居个数k、查询半径r、数据维度以及窗口大小S变化对查询时间和过滤数量的影响.其中,固定设置查询阈值为0.6,具体参数如表3所示. 表3 参数设置Tab.3 Parameter setting 图3为查询邻居个数k对算法性能的影响.随着k值的增大,3种算法都需要消耗更多的查询时间并且过滤数量都相应减少.主要是因为k值的增大导致离群点数目增多,使得算法的计算成本相对增加.通过对比发现,FOD_OUDS算法的查询时间明显低于另外2种算法,这主要是因为FOD_OUDS算法的离群概率值计算可以尽最大可能地避免全近邻集合的迭代计算,从而有利于非离群点的高效过滤使得整体查询时间较短. 图3 参数k对算法的影响Fig.3 The effect of k for the algorithm 图4为查询半径r对算法性能的影响.随着r值的增大,几种算法都需要消耗更多的查询时间.在过滤数量上,随着r值增大,PCUOD算法的过滤数量逐渐减少,FOD_OUDS算法和WDPA算法的过滤数量逐渐增多.对于PCUOD算法,由于其过滤性能的减弱将直接导致其计算成本增大;对于WDPA算法,由于在批量过滤时不可避免地需要近邻空间查询,所以利用网格索引结构维护多维数据会产生非常高昂的空间查询代价.相对来说,FOD_OUDS算法利用分层次划分索引在空间查询代价相对较低且批量过滤时并不需要近邻空间查询,所以性能相对较好. 图4 参数r对算法的影响Fig.4 The effect of r for the algorithm 图5为数据维度变化对算法性能的影响.随着维度的增大,算法的查询时间都明显增大,过滤性能也都减弱.主要是因为随着维度的增大,空间搜索和索引更新都将更加耗时,但是FOD_OUDS算法的处理性能相对较优,主要是因为FOD_OUDS算法所采用的索引在多维数据中的搜索能力和更新性能相对较好,并且通过增加索引结构中的部分存储信息,在一次索引映射中就可以直接完成数据点的批量过滤,也使得其查询时间大幅减少. 图5 维度对算法的影响Fig.5 The effect of dimensionality for the algorithm 图6为窗口大小变化对算法性能的影响.随着窗口增大,算法的查询时间都明显增多,这是因数据量的增多增加了计算成本.同时,过滤数量也明显增多,主要是因为随着数据量的增大导致非离群点数目逐渐增多,使得几种算法均容易满足过滤条件.但是,整体性能上FOD_OUDS算法较优. 图6 窗口大小对算法的影响Fig.6 The effect of window size for the algorithm 综上所述,FOD_OUDS算法在针对不确定数据流环境中的离群点检测问题上的检测时间更短并且过滤性能更优,从而验证了本文提出的FOD_OUDS算法的有效性与高效性. 本文针对不确定数据流环境中的离群点查询问题,提出了FOD_OUDS算法.首先,采用分层次划分思想给出了索引构建策略,使其具备良好的过滤性能.然后,在分析了不确定数据点的离群概率值求解的递推规律后,提出了优先过滤非离群点的概率值求解方法,从而加快了过滤速度.其次,给出了动态维护的更新方法,以减少更新过程中的必要计算代价,从而提高了算法的运算效率.最后,通过实验验证了FOD_OUDS算法具有较高的查询效率与较好的过滤性能.
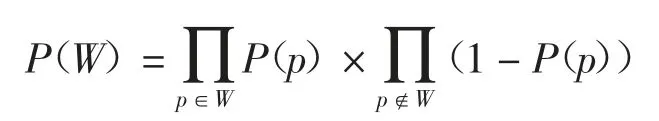

1.2 不确定数据流上的离群点检测处理
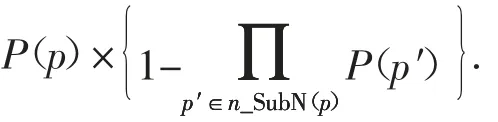

1.3 算法描述


2 实验分析
3 结论
