缩小样本空间——解决条件概率问题的钥匙

龚卫东(特级教师)

条件概率的概念及相关计算公式在高中数学《选修2-3》中以较小的篇幅进行了简单介绍,但却是高中数学学习的难点,高考中偶有涉及,学生得分情况不尽人意．主要原因是学生没有深刻领会“条件”发生后的影响,将样本空间与条件发生前的样本空间混为一谈,如著名的三门问题,生男孩女孩问题等．

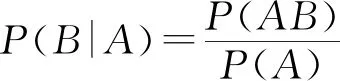
图1

对定义给出的公式如果不能透彻理解,生搬硬套,就会产生很多疑问,从而得出如“抓阄先后概率不同”等荒谬结论．本文结合教学实际经验,给出基于韦恩图(如图1)总结解决条件概率问题的方法，即根据条件,缩小样本空间,在新样本空间中求后发生事件的概率．

例1从一副不含大小王的52张扑克牌中不放回地抽取2次,每次抽1张,已知第一次抽到A,求第二次也抽到A的概率.

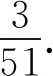
例2老王向老张介绍“这是我女儿”,老张问“你有几个孩子?”老王答“3个”.求老王有儿子的概率.

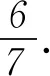
例3(2014年新课标卷Ⅱ理5) 某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,那么随后一天的空气质量为优良的概率是( )．

A. 0.8 B. 0.75

C. 0.6 D. 0.45

解析 设一天的空气质量为优良是事件A,连续两天为优良是事件B,如图1，本题所求的事件中，B一定是A的真子集，A是B的条件,则

例4(2015年北京卷文17) 某超市随机选取1 000位顾客,记录了他们购买甲、乙、丙、丁四种食品的情况,整理成统计表，如表1所示.其中“√”表示购买,“×”表示未购买.

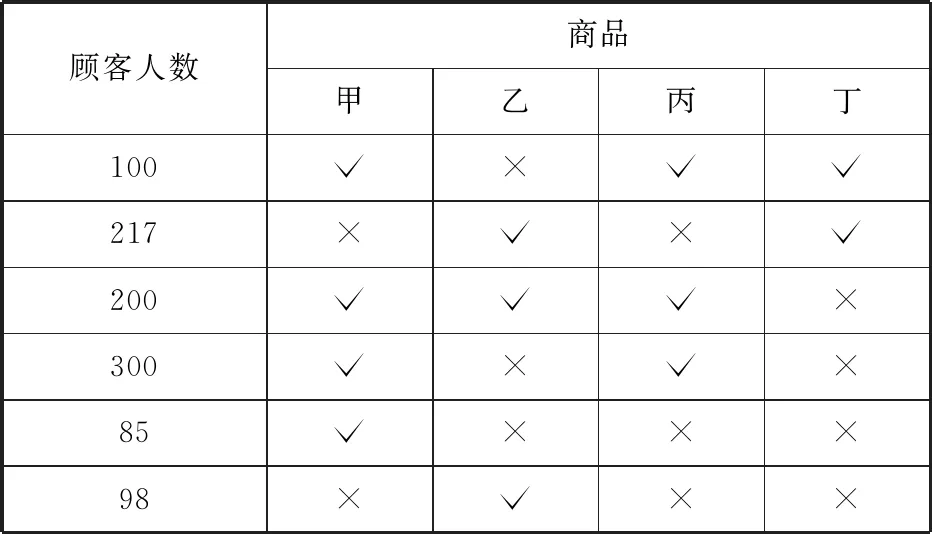
表1

(1)估计顾客同时购买乙和丙的概率；

(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；

(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品可能性最大？

解析 (1)0.2； (2)0.3(具体求解过程略).

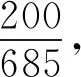
因此,顾客购买了甲,该顾客同时购买丙的可能性最大.

例5(2016年全国卷Ⅱ理18)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度的出险次数的关联如表2所示.

表2

设该险种一续保人一年内出险次数与相应概率如表3所示.

表3

(1)求一续保人本年度的保费高于基本保费的概率;

(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率.

解析 (1)设A表示事件:“一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故

P(A)=0.2+0.2+0.1+0.05=0.55.

(2)设B表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故

P(B)=0.1+0.05=0.15.

又P(AB)=P(B),故

例6有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8,在这批种子中随机抽取一粒,则这粒种子能成长为幼苗的概率是( ).

解析 本题中,设“发芽率”为事件A,出芽后的幼苗成活率0.8是条件概率P(B|A),“这粒种子能成长为幼苗”的含义是“发芽且长成幼苗”,其概率是P(AB),代入公式可得P(AB)=0.72,故选A.

由此可见,利用韦恩图能够帮助学生很好地理解条件的作用,条件越多,新样本空间越小,后发事件在新样本空间中的概率就会变大．以上问题基本囊括高中阶段条件概率涉及的问题类型,基于韦恩图,深刻理解条件,主动缩小样本空间,就获得了解决条件概率问题的钥匙．