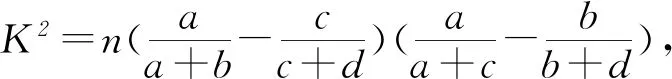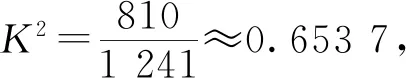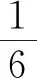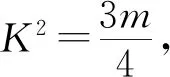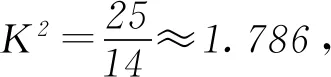独立性检验的诠释与备考
2020-02-29甘大旺特级教师
甘大旺(特级教师)
在各个版本最新的高中数学教材中,统计内容的份量均再一次增加,但相应的学法研究、复习辅导并没有随之“升温”.因此,本文就高中概率统计的一个知识点“独立性检验”进行诠释,例谈其在高考备考中的应用.
1 知识诠释
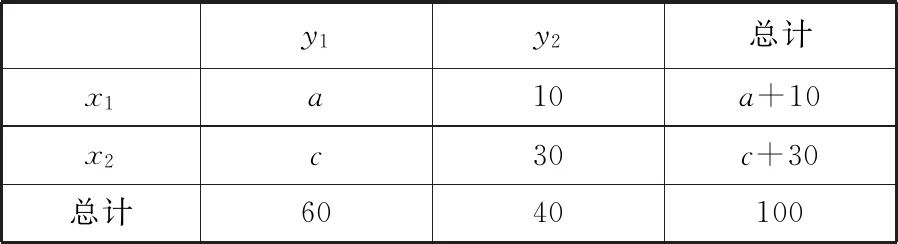
独立性检验是统计学中两种卡方检验之一,高中数学中独立性检验的第一步是依题意完善或作出2×2列联表,如表1所示.
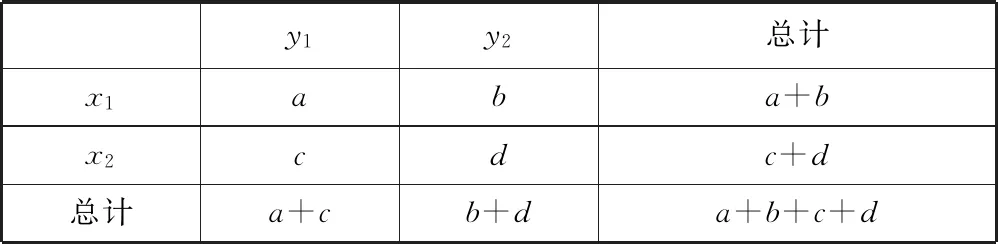
表1
其中,x1,x2是一类变量X的两个互斥状态,y1,y2是另一类变量Y的两个互斥状态,a,b,c,d是分别具有状态x1与y1,x1与y2,x2与y1,x2与y2的样本频数,且都要求频数均不小于5.
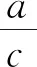
诠释2改变列联表中第2行与第3行的位置、第2列与第3列的位置,都不会改变随机变量K2值的大小,如下列3种变换(如图1),也分别满足
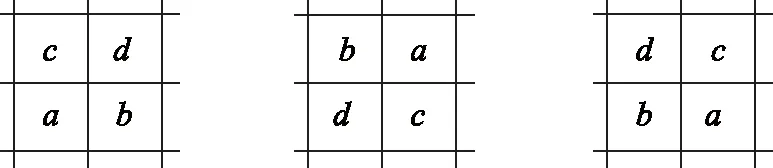
图1
(cb-da)2=(ad-bc)2,
(bc-ad)2=(ad-bc)2,
(da-cb)2=(ad-bc)2.
高中独立性检验的第三步是根据下列统计学上的概率临界值表,间接判定两类变量“X与Y有关系”的可信程度(如表2).
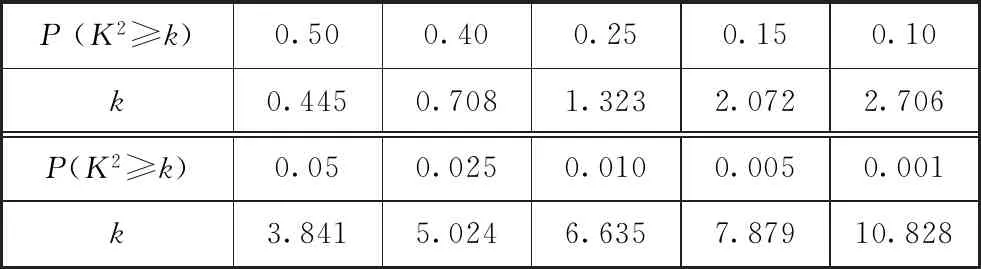
表2
诠释3因为独立性检验的基本思想类似于反证法,所以直接用所算K2值对比表2中临界值k就可查找两类变量“X与Y有关系”出错的至多概率,从而“X与Y有关系”判断正确的至少概率(把握性)是1-P(K2>k).
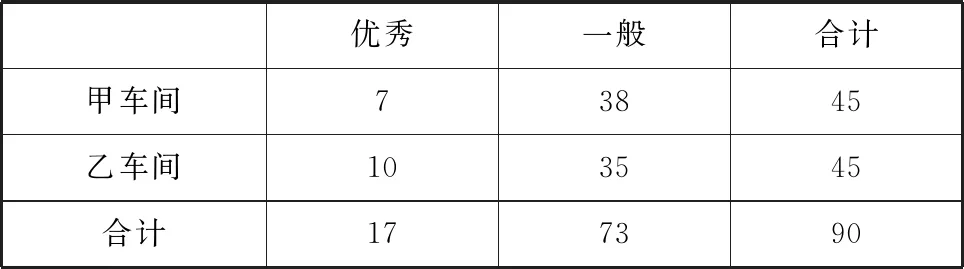
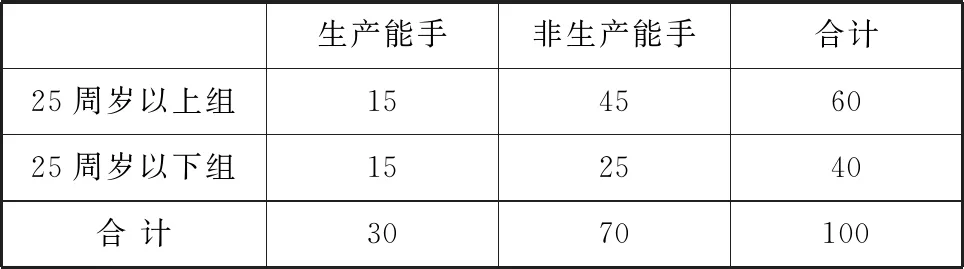
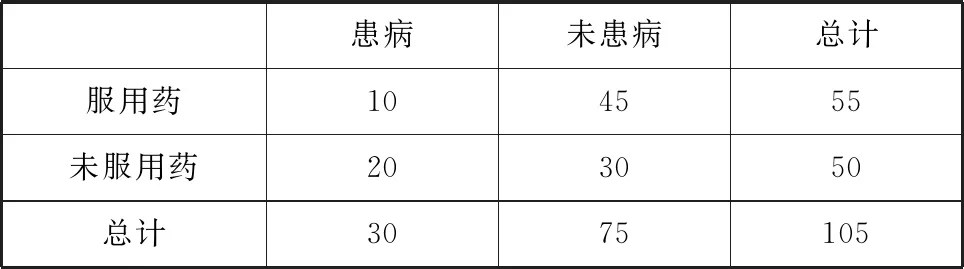
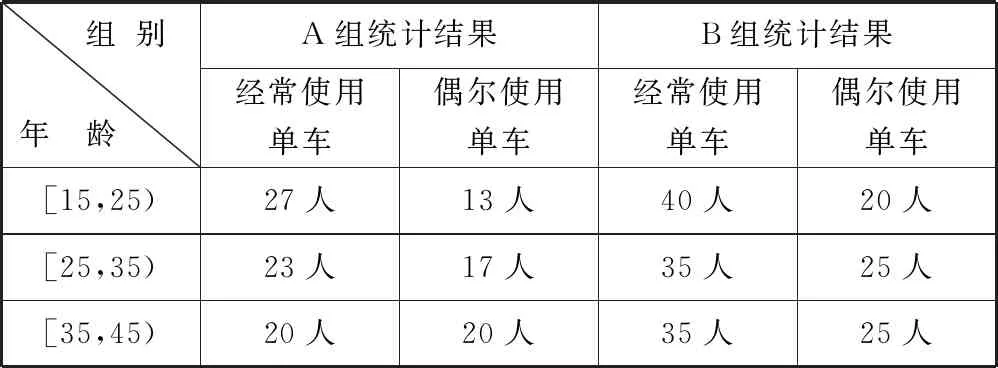
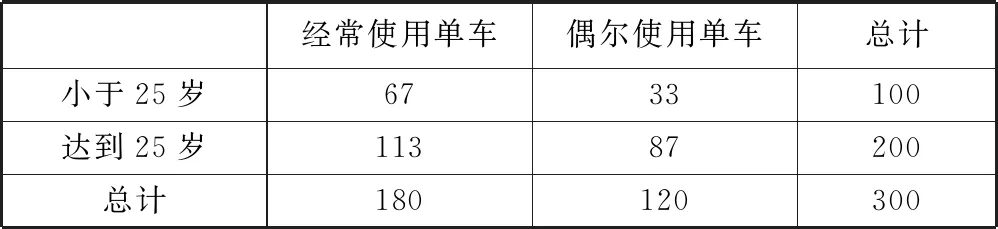
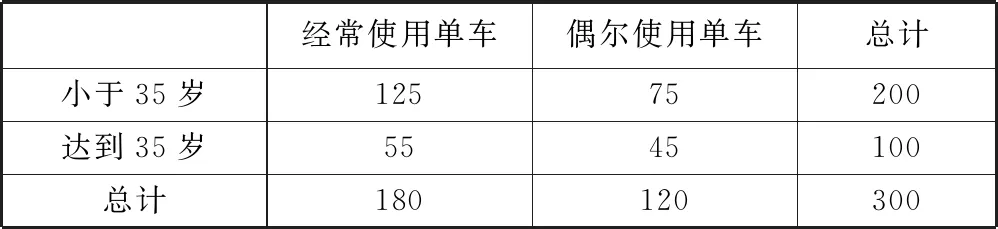
诠释4借助概率临界值表,可以逆向延伸和理解K2 例1为了考察某种药物预防疾病的效果,进行动物试验,得到如表3所示的药物效果与动物试验的列联表. 表3 由以上数据给出以下结论:① 能在犯错误的概率不超过0.05的前提下认为药物有效;② 不能在犯错误的概率不超过0.025的前提下认为药物有效;③ 能在犯错误的概率不超过0.010的前提下认为药物有效;④ 不能在犯错误的概率不超过0.005的前提下认为药物有效. 其中,正确结论的个数是________. 解析 根据列联表,计算得 查概率临界值表知,结论①成立的充分条件是K2≥3.841,所以结论①正确;结论②成立的充分条件是K2<5.024,所以结论②错误;结论③成立的充分条件是K2≥6.635,所以结论③错误;结论④成立的充分条件是K2<7.879,所以结论④正确. 综上所述,正确结论的个数是2. 点评 查阅独立性检验的概率临界值表时,要贴近实际问题,看准、看懂、用准“有关”或“无关”“出错误”或“有把握”“至少”或“至多”等关键词. 例2某共享单车经营企业欲向某市投放单车,为制定经营策略,该企业在已经投放单车的乙市分两组进行随机调研,针对15至45岁的人群,按比例随机抽取300份问卷,统计结果见表4. 表4 (1)从统计数据可直接得出“是否经常使用共享单车与年龄界限(记作m岁)有关”的结论,在用独立性检验的方法说明该结论正确时,为使犯错误的概率尽量小,年龄m应该取25还是35?请说明理由. (2)对于(1)中所取的年龄界限m的值,大约有多少把握认为“经常使用共享单车与年龄达到m岁有关”? 解析 (1)取m=25,整理数据绘制列联表(如表5所示). 表5 再取m=35,整理数据绘制列联表(如表6所示). 表6 点评 对于两类分类变量X与Y的2×2列联表,相应算出的K2越大(小),判定“X与Y有关”的出错概率就越小(大),即认为“X与Y有关”的把握性就越大(小). 练习1如果两个分类变量X与Y的2×2列联表如表7所示. 表7 对于同一样本,以下数据说明X与Y有关系的可能性最大的一组是( );可能性最小的一组是( ). A.a=45,b=15 B.a=40,c=20 C.a=35,c=25 D.a=30,c=30 练习2某工厂两个车间的工人在一次技术比赛中的成绩,可以绘制成列联表(如表8). 表8 于是,推断“比赛成绩与车间有关系”错误的概率属于区间( ). A. (0.3, 0.4) B. (0.4, 0.5) C. (0.5, 0.6) D. (0.6, 0.7) 练习4某制造企业有25周岁以上(含25周岁)职工300名,25周岁以下职工200名.为调查职工的日平均生产量是否与年龄有关,现从中分层抽取了100名职工,先统计了他们某月的日平均生产件数,然后按员工年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组职工的日平均生产件数分成5组分别进行统计,得到如图2所示的频率分布直方图.企业授予日平均生产件数至少80件的职工为“生产能手”. 图2 (1)绘制职工类别(“生产能手”与“非生产能手”)与年龄的2×2列联表; (2)试问:有多大的把握认为“生产能手与所在的年龄组有关”? 提示:(1)“25周岁以上”年龄组有60人,“25周岁以下”年龄组有40人,再对照两个频率分布直方图,绘制2×2列联表,如表9所示. 表92 备考举例
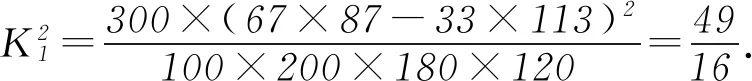
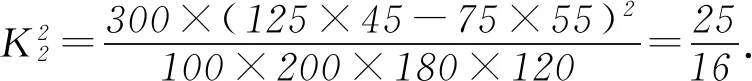

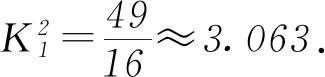
3 备考练习