大气湍流下圆偏振调制性能研究

张莉, 汪井源, 郑吉林, 张晗, 蒲涛∗

(1 南京邮电大学电子与光学工程学院微电子学院, 江苏 南京 210023;2 陆军工程大学通信工程学院, 江苏 南京 210007;3 中船重工724 研究所, 江苏 南京 211153)

1 引 言

与传统的开关键控(OOK)和相位移位键控(PSK)调制方式相比,POLSK 调制对相位噪声具有较强的抗干扰能力而且不受频率啁啾的影响[5,7]。圆偏振移位键控调制(CPOLSK)是在POLSK 调制的基础上提出来的,与POLSK 调制相比主要有两方面的优点:一是无需发送端和接收端对准;二是圆偏振光在经历粒子散射时,光强分布更加均匀[4]。理论和实验结果表明,激光圆偏振在大气信道中的状态变化不大,圆偏振调制技术可以提高自由空间光通信系统的性能[8]。文献[4]分析了OOK、脉冲位置调制(PPM)等强度调制的包误码率与信噪比的关系,得出CPOLSK 的性能最优。文献[9,10]将POLSK 调制方式与光码分多址(OCDMA)技术相结合用于FSO 湍流信道系统中,得出POLSK-OCDMA 方式的误码性能优于OOK-OCDMA 的结论。文献[11]提出将POLSK 调制方式与波分复用(WDM)FSO 系统结合来提高通信容量,仿真分析了不同湍流强度条件下POLSK 和幅度移位键控(ASK)两种调制方式的误码率与接收功率的关系,结果表明,基于POLSK 调制的WDM-FSO 系统的性能优于ASK 调制。目前,FSO系统湍流模型主要有对数正态分布(LN)和双伽马(Gamma-Gamma)分布模型,其中LN 模型适应于弱湍流,Gamma-Gamma 模型适应于中强湍流[12～14]。文献[15]利用LN 和Gamma-Gamma 模型对OOK 调制FSO 通信系统的平均信道容量进行了研究,仿真分析了大气湍流强度、波长和传输距离与信道容量的关系。文献[16]在同时考虑大气湍流和瞄准误差的条件下利用Gamma-Gamma 模型对OOK 调制FSO通信系统的平均信道容量做了进一步研究。文献[17,18]利用Gamma-Gamma 模型分别研究了直接接收和相干接收CPOLSK 系统的误码率与信噪比的关系,同时对中断概率也进行了分析。文献[10,19]利用Gamma-Gamma 模型对POLSK-WDM-FSO 系统进行了研究。文献[20]对基于CPOLSK 调制的空-地FSO 通信系统的性能进行了分析,基于从日本通信卫星OICETS 上测量到的斯托克斯参数数值,对系统的性能进行了评估并与OOK 调制方案的性能进行了比较。文献[21]分析了大气湍流和瞄准误差联合效应下OOK 调制FSO 系统的性能,但是没有对孔径平均效应对系统性能的影响进行研究。

本文结合孔径平均技术,对大气湍流和瞄准误差联合效应下CPOLSK 调制的FSO 系统性能进行了研究。基于MeijerG 函数,推导了CPOLSK 调制误码率和中断概率的闭合表达式。仿真分析了归一化波束宽度、归一化抖动标准差以及接收孔径对系统误码率和中断概率性能的影响,并与OOK 调制的误码率性能进行了比较。利用蒙特卡洛方法对其数值仿真得到的结果进行了验证。

2 信道模型

在同时考虑湍流效应和瞄准误差的条件下,信道状态可以表示为[16]

式中ha表示大气湍流效应引起的衰减,hp表示瞄准误差引起的衰减。

ha的概率密度函数采用Gamma-Gamma 分布模型,可表示为

式中Kυ(·)为第二类贝塞尔函数,Γ(·)为Gamma 函数。在平面波情况下,α 和β 分别表示为[22]

661 Prevalence of skin diseases among marine-training soldiers stationed in east coastal area and its influencing factors

式中fh/ha(h/ha)为大气湍流衰减ha存在下的条件概率密度函数,其可表示为

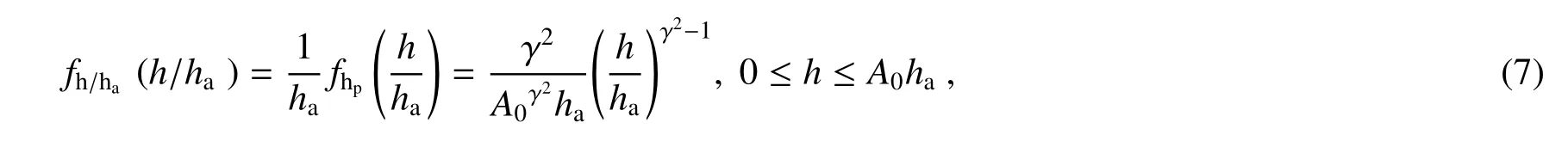
将(2)式和(7)式代入(6)式,得

由MeijerG 函数[24]知

代入(8)式并根据文献[24]进行化简得

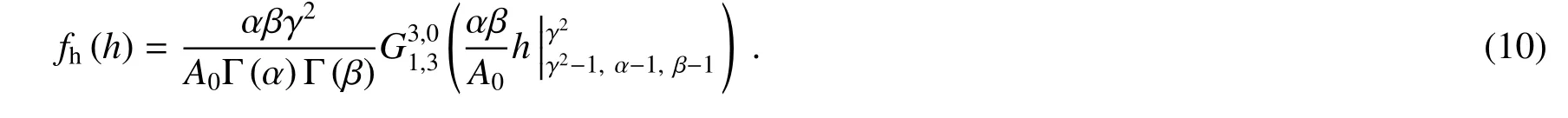
3 性能分析

3.1 误码性能

根据文献[4]中给出的调制解调方案,可以得到OOK 调制和双路差分接收CPOLSK 调制在无光强闪烁条件下的误码率分别为

式中R 为光电转换效率,Pr为接收光功率,σn为信道噪声方差。

在光强闪烁存在的情况下,OOK 和CPOLSK 调制的条件误码率为

平均误码率为

令平均信噪比RSN= R2Pr2/σn2,将(10)式代入(15)、(16)式,并利用MeijerG 函数[24]对其求解闭合表达式,可得

而(17)、(18)式就是两种调制方式下平均误码率的闭合表达式。

3.2 中断概率性能

中断概率主要用来评价系统的可靠性,它是指系统误码率大于某一目标误码率的概率,也就是信噪比低于某一值时的概率[21,25]。设γth0为信噪比的门限值,根据文献[4]的双路差分接收方案,CPOLSK 调制方案的信噪比为

则根据上述中断概率的定义,CPOLSK 调制的中断概率可以表示为

将(19)式代入(20)式得

即

式中RSN/(2γth0)为归一化门限值[25],记为γth,且

将(10)式代入(23)式得

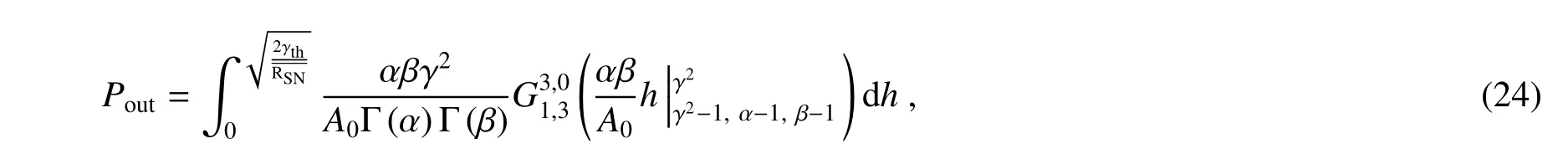
利用MeijerG 函数[24]得CPOLSK 调制方式下中断概率的闭合表达式

4 结果分析与讨论

4.1 误码率性能

Fig.1 为接收尺寸D=5 cm,归一化抖动标准差σs/r 分别取值为0.5、1、2 时,归一化波束宽度ωz/r与平均误码率(BER)之间的关系,并给出了OOK 调制和CPOLSK 调制的性能对比图。由Fig.1 可见,当σs/r = 0.5,在ωz/r=2 附近误码率有最小值;当σs/r = 1,在ωz/r=4 附近误码率有最小值;当σs/r = 2,在ωz/r=6 附近误码率有最小值。即归一化波束宽度对系统性能的影响是非线性的,存在最优值。

Fig.2 为D = 5 cm、ωz/r=2,不同信噪比条件下归一化抖动标准差与平均信噪比之间的关系。随着归一化抖动标准差的增大,平均信噪比也随之增大。

Fig.1 Average BER versus the normalized beamwidth and the normalized jitter

Fig.2 Average BER versus the normalized jitter and the average RSN

Fig.3 为D=1、5、10 cm 时,平均信噪比与误码率之间的关系,并给出了OOK 调制和CPOLSK 调制的性能对比图,其中,1 km 处波束的宽度ωz= 10 cm,瞄准误差偏移量标准差σs= 2.5 cm。在同一孔径尺寸条件下,CPOLSK 调制的误码率性能优于OOK 调制。Table 1 给出了平均信噪比为50 dB 时不同方案下误码率性能的对比关系。从Table 1 可以得出:不同接收尺寸条件下,CPOLSK 调制的性能均优于OOK 调制。同一调制方式下,5 cm 孔径接收机的误码率性能比1 cm 孔径提升了3 ～4 个数量级,10 cm孔径接收机的误码率性能比1 cm 孔径提升了7 ～8 个数量级。提高接收孔径尺寸可以有效地提高系统的性能。数值计算结果与蒙特卡洛仿真拟合较好,说明了数值计算结果的正确性。

Table 1 Average BER versus the receiving aperture size with OOK and CPOLSK modulation

4.2 中断概率性能

Fig.4 为D = 5 cm,归一化抖动标准差σs/r 分别取0.5、1、2 时,CPOLSK 调制方式下归一化波束宽度ωz/r 与中断概率之间的关系。从Fig.4 中可以看出,当σs/r = 0.5,在ωz/r=2 附近中断概率有最小值;当σs/r =1,在ωz/r=3 附近误码率有最小值;当σs/r =2,在ωz/r=4 附近中断概率有最小值。

Fig.5 为接收尺寸D = 5 cm、ωz/r=2 时,不同信噪比条件下CPOLSK 调制方式归一化的抖动标准差与中断概率之间的关系。随着归一化抖动标准差的增大,中断概率不断增大,并趋近于1。

Fig.6 为D = 2、5、10 cm 时,CPOLSK 调制方式下,归一化阈值信噪比与中断概率之间的关系,其中,1 km 处波束的宽度取值ωz为7.5 cm,瞄准误差偏移量标准差σs取值为2.5 cm。Table 2 给出了归一化阈值信噪比为30 dB 时不同方案下中断概率性能的对比关系。从Table 2 可以得出:5 cm 孔径接收机的中断概率性能比2 cm 孔径提升了1 个数量级,10 cm 孔径接收机的中断概率性能比2 cm 孔径提升了4 个数量级。提高接收孔径尺寸可以有效地提高系统的中断概率性能。数值计算结果与蒙特卡洛仿真拟合较好,说明了数值计算结果的正确性。

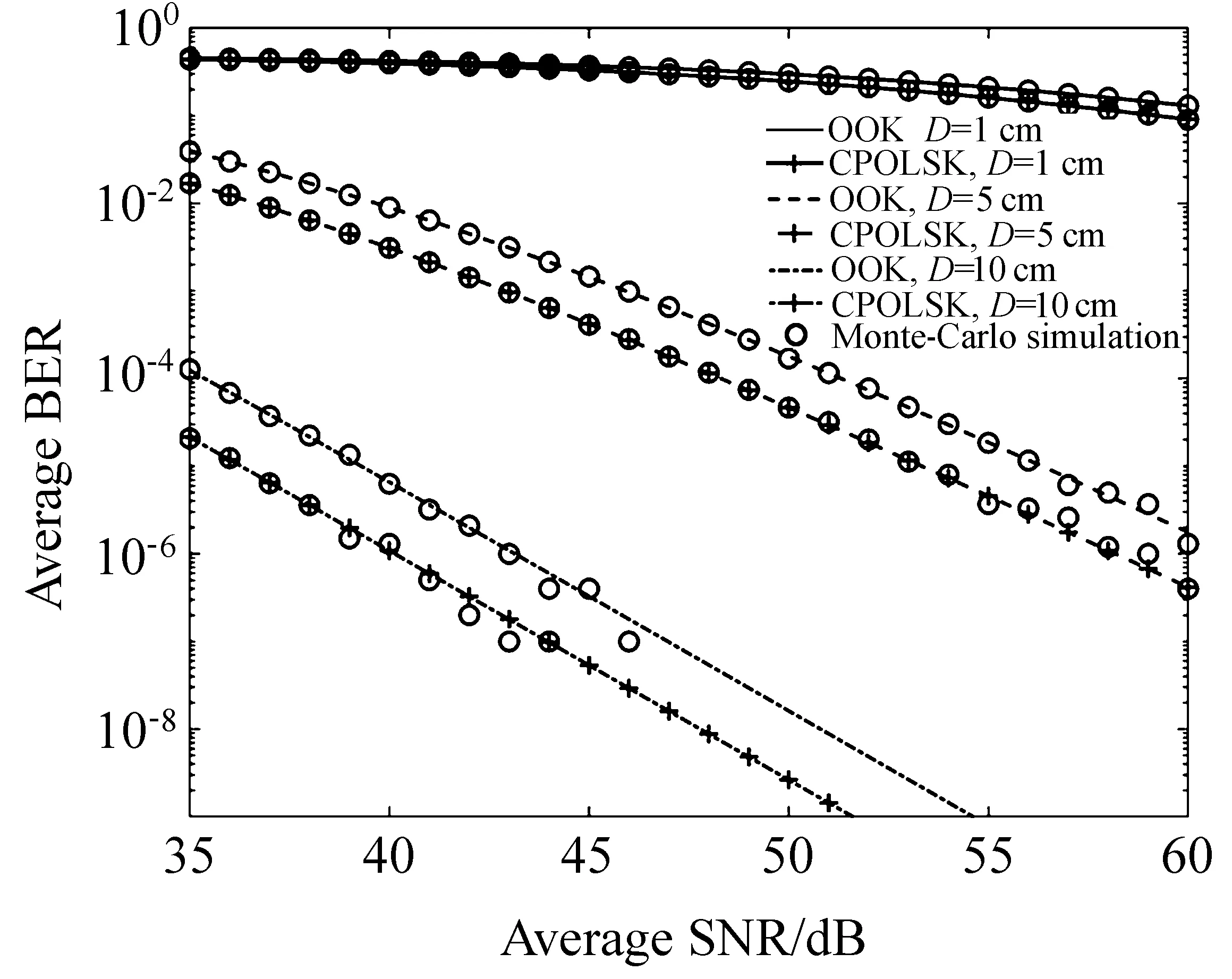
Fig.3 Average BER versus the average RSN and the receiving aperture size

Fig.4 Average BER versus the normalized beamwidth and the normalized jitter

Table 2 Average BER versus the receiving aperture size with CPOLSK modulation

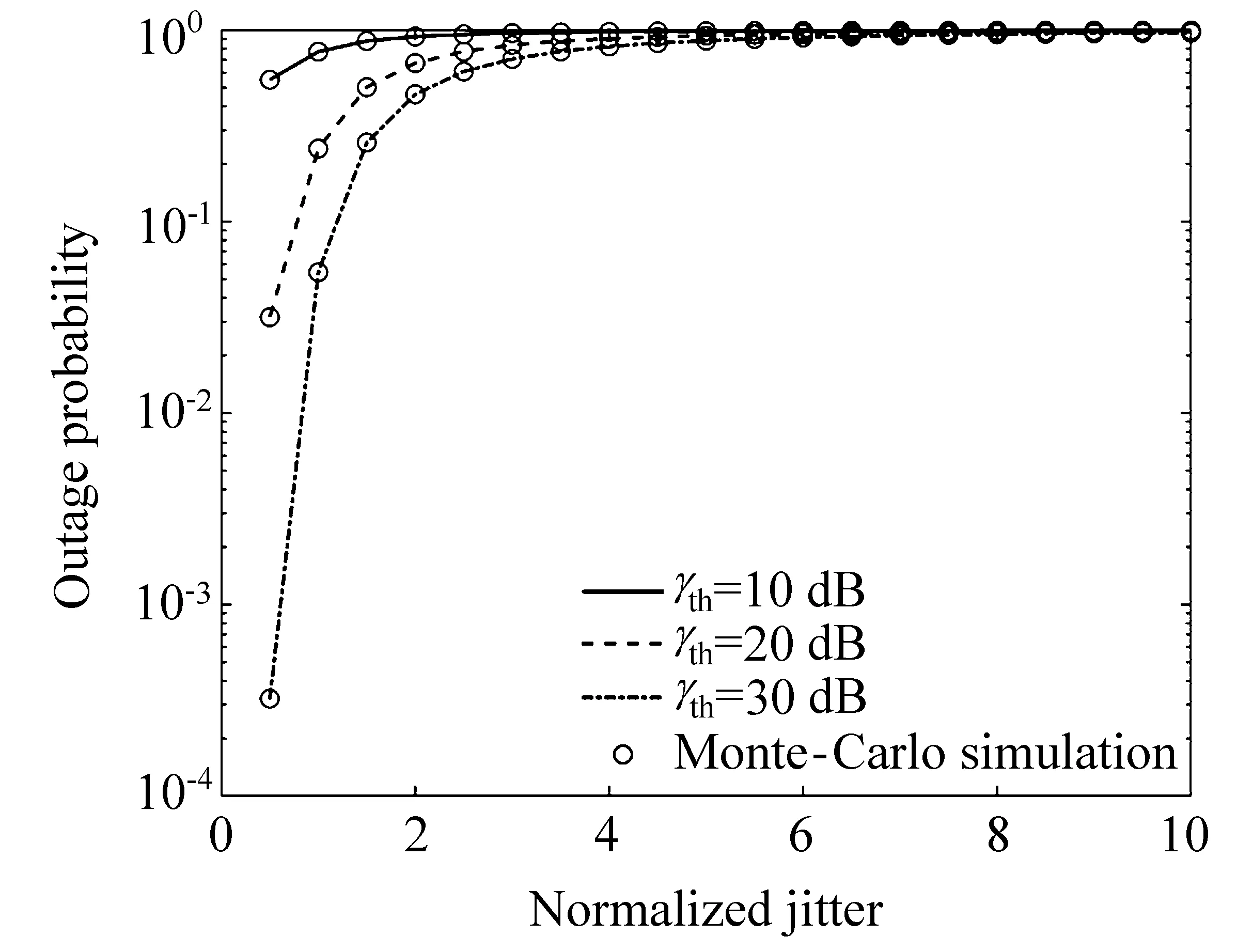
Fig.5 Outage probability versus the normalized jitter and the normalized threshold

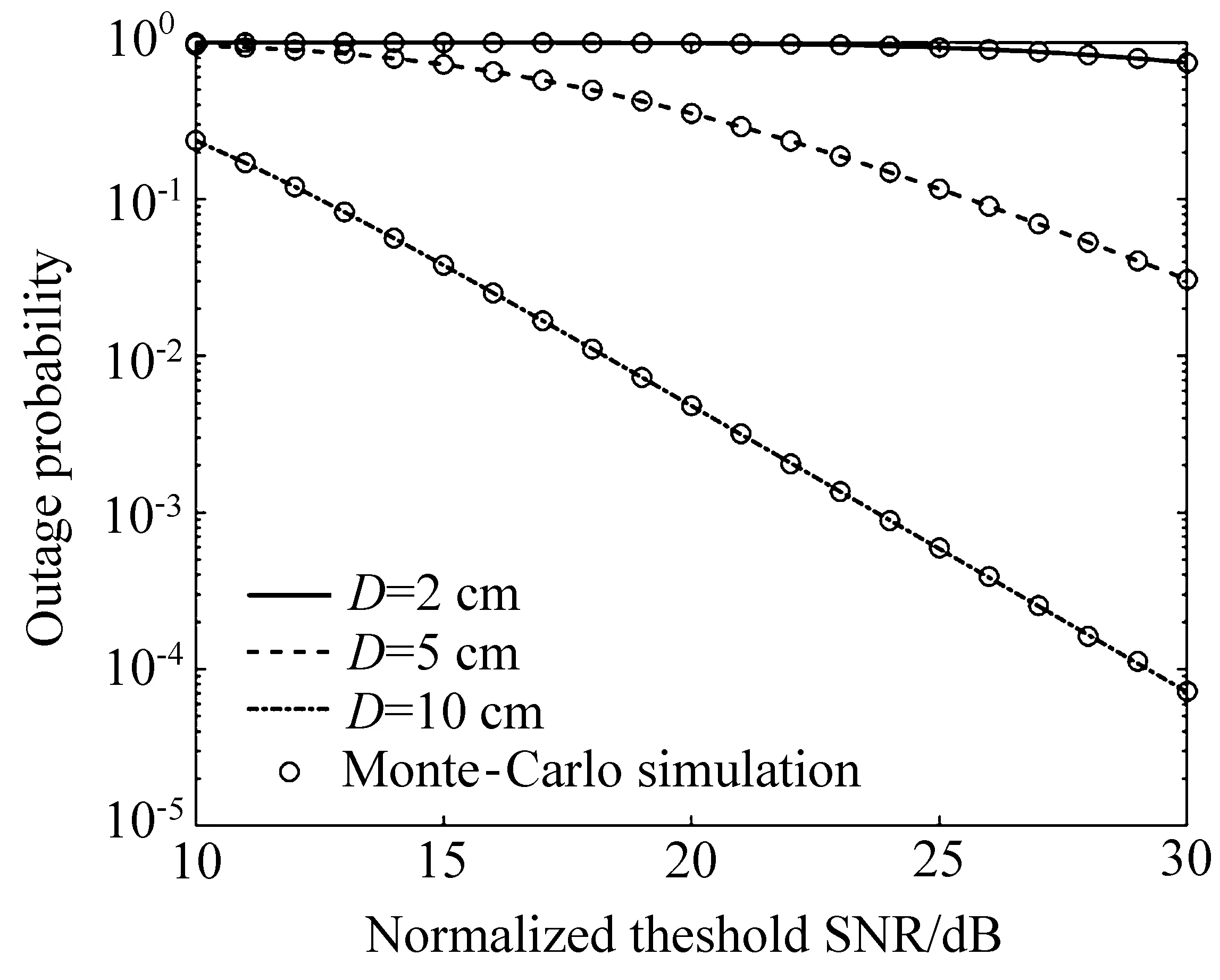
Fig.6 Outage probability versus the normalized threshold and the receiving aperture size

将蒙特卡洛方法得到的结果与数值仿真分析结果进行对比,验证了基于偏振调制的FSO 系统性能数值仿真分析结果的正确性。由于蒙特卡洛方法运行比较耗费时间,在运用该方法进行数值仿真结果验证时,实验点选取为107,通过产生符合Gamma-Gamma 分布模型和瞄准误差模型的随机变量并根据系统误码率性能和中断概率性能的理论分析过程,完成蒙特卡洛仿真。

5 结 论

采用孔径平均技术提高湍流和瞄准误差联合信道模型下的CPOLSK 调制误码率和中断概率性能。仿真研究了归一化波束宽度、归一化抖动标准差以及接收孔径对系统误码率和中断概率的影响,并与OOK 调制的误码率性能进行比较。利用蒙特卡洛方法对基于偏振调制的FSO 通信系统性能的数值仿真结果进行了验证。结果表明：同一条件下,CPOLSK 调制的误码率性能优于OOK 调制;归一化波束宽度对系统性能的影响是非线性的,存在最优值;随着归一化抖动标准差的增大,系统的性能会下降;增大接收孔径尺寸,可以有效地提高系统的性能。研究结果对FSO 通信系统的设计具有实际指导意义,后续会开展相关实验,进一步推动CPOLSK 调制方式在FSO 通信系统中的应用。