非马尔科夫环境对海森堡XXZ自旋链模型中量子隐形传态的影响

迪丽达尔·海依提江, 阿拉帕提·阿不力米提, 白慧婷, 阿依尼沙·牙生,艾则孜古丽·阿不都克热木, 艾合买提·阿不力孜

(新疆师范大学物理与电子工程学院, 新疆 乌鲁木齐 830054)

1 引 言

在实际的物理环境中量子通讯成为了研究热点,其中量子纠缠扮演着重要角色,其在量子隐形传态中展现出的神奇特性以及潜在的应用价值激起了人们的极大兴趣[1,2]。然而在实际的物理环境中,不存在真正意义上的封闭系统,任何量子系统都将与无法控制的环境相互作用,这些受环境或其它自由度影响的系统的关联特性降低,其动力学过程可区分为马尔科夫过程和非马尔科夫过程[3,4]。从系统中流向环境的能量和信息不再流回到系统,即此过程为系统对历史没有记忆的马尔科夫过程。然而,实际环境和系统强耦合或者环境是人为构造的情况[5]普遍存在,流入到环境的能量和信息流回到系统中去,该过程必然改变系统的状态和性质,因此必须考虑非马尔科夫效应。在某种程度上,虽然马尔科夫过程能够较为准确地描述开放量子系统的某些动力学演化特性,但是由于其表示形式太过简单,可能会导致理论计算与实际的物理情况不相符,甚至有可能会漏掉一些比较重要的动力学性质[6～8]。因此,研究有记忆效应的非马尔科夫过程的动力学演化特性非常重要。

Laine 等[9]发现,用纠缠光子极化态进行量子隐形传输时,即使是在混合光子极化态情况下,由两个光子的局域环境间存在的初始关联记忆效应能够使得完美量子隐形传态成为可能。到目前为止,量子隐形传态已在很多不同体系中实现,如具有易集成性和可扩展性特点的固态体系[10,11]。然而,固态体系因与周围环境耦合自由度多,退相干效应也比较强。如何克服固态体系中的退相干效应是一个极具实际意义的课题,固态体系与其环境耦合强的特点带来的非马尔科夫性已被用来在一定程度上解决该问题。比如,Diosi 等[12,13]提出量子态扩散方法,可以用来探索开放量子系统的非马尔科夫动力学。文献[14～16]利用量子态扩散方法(Quantum state diffusion,QSD)研究了两个二能级原子与一个共同玻色库强耦合的模型,结果证实两个非相互作用的量子位的纠缠完全是由环境记忆产生的。调研发现,利用此方法研究开放量子系统的动力学问题仅局限于量子纠缠,因此可利用此方法研究开放量子系统的量子通讯特性。

本文第2 节引入一对耦合的量子比特模型,并介绍了QSD 理论方法[14,17]。第3 节介绍量子隐形传态基础理论。第4 节重点利用QSD 方法探究海森堡自旋链被用来当量子隐形传态信道时,零温玻色库环境的非马尔科夫性对隐形传态保真度的作用。此外,根据海森堡自旋链实际应用情况,理论分析了在非马尔科夫环境下外加磁场及DM 相互作用对隐形传态的作用,前者可以用来实现各种量子逻辑门操作,而后者作为一种自旋-轨道耦合相互作用已被用于操控自旋链体系中的量子纠缠。

2 模型与量子态扩散方法

考虑两比特海森堡XXZ 模型(等效于一对耦合的二能级原子)与零温玻色库相互作用,总哈密顿量表示为(设ħ=1)

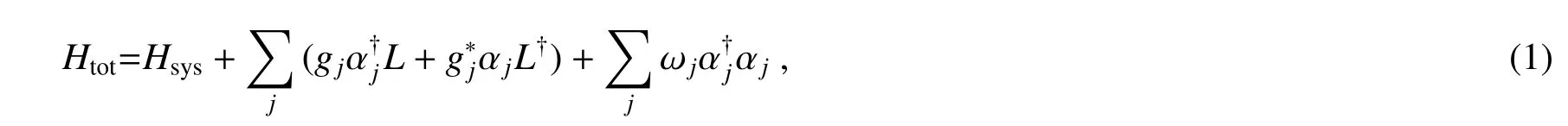
式中L=kAσ1−+kBσ2−是系统与环境耦合的Lindblad 算符,kA、kB是常量,描述两个自旋链与各自环境的不同耦合强度;Hsys选为含z 方向的DM 相互作用和外加磁场的海森堡自旋链哈密顿量,可写为

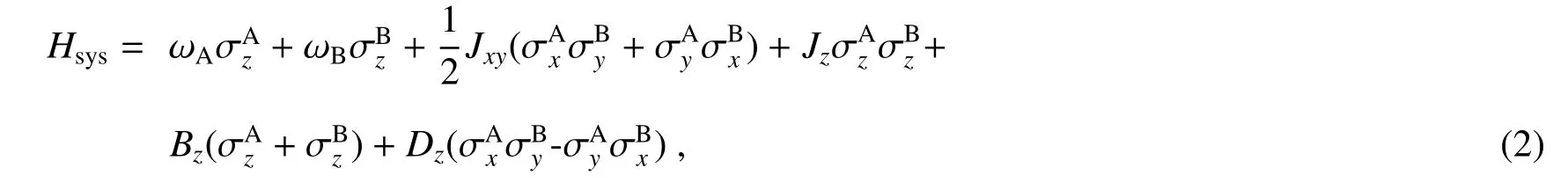
式中J 为x、y、z 方向上的耦合常数,此处取Jx= Jy= Jxy;σ±= (σx±iσy)/2 为二能级原子的产生(湮灭)算符;ωA和ωB为两个原子的能级跃迁频率;Bz为z 方向均匀外加磁场;Dz代表z 方向DM 相互作用,它源于自旋与轨道之间的耦合。

基于海森堡模型所产生的纠缠在量子信息传输等领域中扮演着重要角色,尤其是包含Dzyaloshinskii-Moriya(DM)相互作用的海森堡自旋链的纠缠特性备受关注[18,19]。根据QSD 理论,相互作用自旋系统的非马尔科夫随机扩散方程(NMQSD)可写为[20]

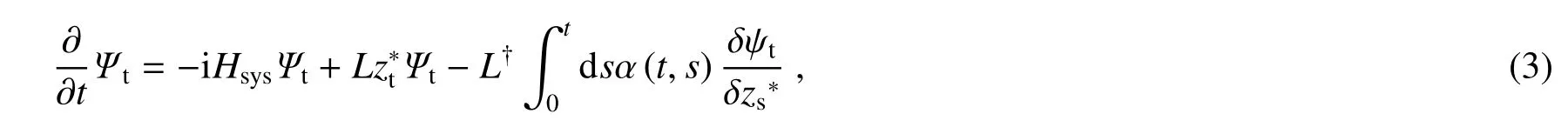
其中M[·] 表示经典噪声zt的系宗平均值。将噪声选为Ornstein-Uhlenbeck 噪声时, 其关联函数为α(t,s) = (γe−γ|t−s|)/2,其中的参数γ 反映库的记忆效应,以γ 的取值就可以区别马尔科夫和非马尔科夫过程。当γ 趋近于无穷时,关联函数是一个Dirac delta 函数,此时系统完全处于马尔科夫环境中,反之处于非马尔科夫环境[17]。

通常可以利用(3)式推导出精确的非马尔科夫近似主方程[17]来求解系统约化密度矩阵ρt,即

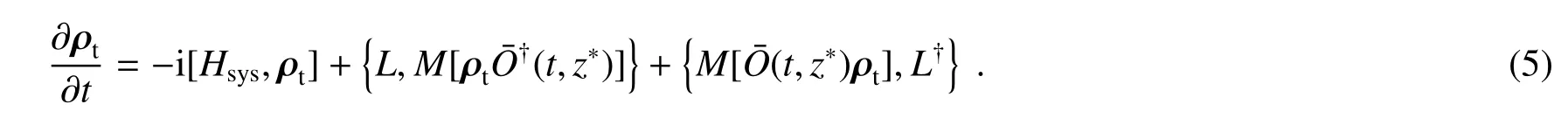
值得一提的是主方程(6)可以很好地替代精确的非马尔科夫主方程(5)[12]。文献[13]发现在实验数据计算时非马尔科夫过程中一阶近似和零阶近似结果相似,尤其在零阶近似中数学计算过程被简化。因此,将通过零阶近似情况下的主方程来求解系统的约化密度矩阵。

3 标准量子隐形传态协议下传递单比特量子态的平均保真度

在标准量子隐形传态协议下[21],以最大纠缠态作为量子信道,如四个Bell 态

中的一个,则作为被传输的信息,任意未知的单粒子纯态可写为

式中0 ≤θ ≤π,0 ≤φ ≤2π。隐形传态后总输出态可以表示为[22]

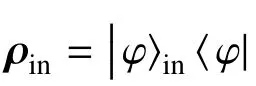
然而,量子隐形传态的输入态是未知的,这更有利于计算量子隐形传态中所有可能被输出态的平均保真度。平均保真度的公式为[24]

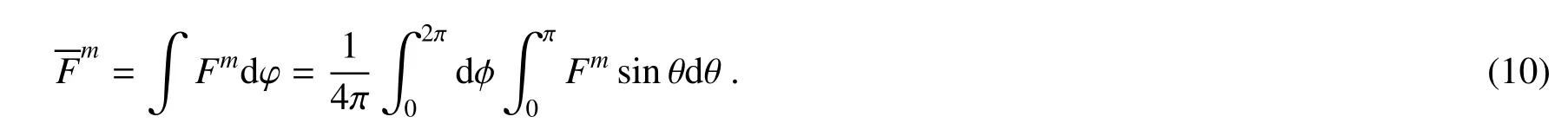
4 数值结果与讨论

基于平均保真度(10)式,利用非马尔科夫近似主方程(6)式进行数值计算,并研究以最大纠缠态为量子信道传输未知量子态时,受环境非马尔科夫性系数γ、耦合常数Jxy、Jz影响的量子通信过程。Fig.1给出了在最大纠缠态量子信道传输过程中,γ 取不同值时平均保真度随时间的演化图像。对于参数的取值,只考虑一个简单的情况,参数都对称的两个qubits,即ωA=ωB=0.5ω,kA=kB=1。当量子信道由最大纠缠态构成时,随着γ 的减小,即非马尔科夫记忆效应增强,F 增大。这是因为原来系统中耗散到环境中的信息和能量部分返回到系统,表明非马尔科夫环境的记忆效应有助于保持和提高隐形传态平均保真度。

Fig.1 Average fidelity for different memory times of the noise. The other parameters are Jxy =1,Jz =0,ωA =ωB =0.5ω,kA =kB =1

Fig.2 Time evolution of average fidelity for different anisotropic coupling parameters in non-Markovian environment. The other parameters are|ψ〉=1/(|01〉+|10〉),ωA =ωB =0.5ω,kA =kB =1. (a) Jz =0;(b) Jxy =1

为进一步弄清非马尔科夫环境中自旋耦合常数对保真度的作用, Fig. 2 给出量子信道由|ψ〉 =1/(|01〉+|10〉)构成时,在非马尔科夫机制下(γ =0.1)耦合常数Jxy、Jz对F 的影响。Fig.2(a)描述了当Jz=0,即该模型退化为海森堡XX 自旋链模型,Jxy分别取不同值时F 随时间的变化关系。由Fig.2(a)可见Jxy= Jz=0 时,这两个非相互作用的量子位的保真度完全受环境记忆的作用,然而随Jxy增大而增大,表明Jxy在隐形传态过程中起着积极的作用。Fig.2(b)显示,在非马尔科夫机制下且取Jxy= 1 时, Jz取值越小越大。也就是说在实际模型中可以选择XX 自旋链模型实现较为理想的隐形传态。

还发现不同的自旋-自旋耦合常数对隐形传态保真度的影响并非总是不变的。如Fig.3,当选取不同

Fig.3 Time evolution of average fidelity for different anisotropic coupling parameters in non-Markovian environment.The other parameters are|ψ〉=1/(|00〉+|11〉),ωA =ωB =0.5ω,kA =kB =1.(a)Jz =0;(b)Jxy =1

Fig.4 Time evolution of average fidelity for different DM interaction and external magnetic field in non-Markovian environment.The other parameters are|ψ〉=1/(|01〉+|10〉),Jxy =1, Jz =0,γ=0.1,ωA =ωB =0.5ω,kA =kB =1.(a)Dz =0;(b)Bz =0;(c)Dz =1;(d)Bz =1

的量子信道时, Jxy与Jz对的影响与Fig.2 正好相反。从图中还可以看出,保真度随时间的震荡幅度及频率也与自旋耦合常数有关。总之,Fig.2 和Fig.3 表明,量子信道的选取影响随时间的演化特性。因此,选择合适的纠缠态作为量子信道尤为关键,环境噪声关联系数γ 和两比特间耦合常数Jxy、Jz可以有效地控制平均保真度。接下来讨论非马尔科夫环境下,均匀外加磁场Bz和DM 相互作用Dz对的影响。Fig.4 给出了当量子信道由纠缠态|ψ〉 = 1/(|01〉+|10〉)构成时, Bz和Dz的引入对量子隐形传态的影响。Fig.4(a)显示,无DM 相互作用时,外加磁场对平均保真度有明显的积极作用。从Fig.4(b)中可以看出没有外加磁场只有Dz时,Dz越大,的频率和振幅同时增大,峰值可达最大值1。为了弄清磁场和DM 相互作用同时存在时随时间的演化特性,给出了Fig.4(c)。发现两者都取相同值时保真度的质量不如一个取值比另一个小的情况。而且两者取值差别越大保真度越好。

5 结 论

利用非马尔科夫QSD 方法研究了在海森堡XXZ 自旋链模型中量子隐形传态的理论实现。详细讨论了环境非马尔科夫性系数、不同的量子信道、两比特间不同的耦合常数、z 方向的DM 相互作用以及均匀外加磁场对平均保真度的影响。研究结果表明: 量子隐形传态的平均保真度随环境的记忆效应的增大,即环境关联系数γ 的减小而增大,说明环境记忆效应对量子隐形传态起到积极作用。另外,不同的量子信道下,不同的自旋耦合常数对量子隐形传态平均保真度的影响不尽相同。最后,如果想得到最大保真度,外加磁场和DM 相互作用不能同时存在。在实际情况下,如两种因素同时存在,通过增大两者取值间差距也可以得到较为理想的保真度。