关于一维XXZ海森堡自旋开、闭链模型关联特性的对比研究

韩文娟, 强睿, 彭定燕

(六盘水师范学院物理与电气工程学院, 贵州 六盘水 553004)

1 引 言

近年来,无序体系所具有的很多力学、磁学特性是理论模拟和实验研究的热点内容,关于其实验结果的理论方法很好地解释了一些合金的热力学性质以及临界行为[1];朗道理论在定性分析物质的相结构时具有很大价值[2]。量子多体关联系统中,量子相变[3]是一种非常重要而奇特的现象,它是由于系统参数改变(如一个外加磁场或耦合常数的改变)而引起的量子涨落,量子相变反映系统基态结构的变化,与系统基态及系统本征态密切相关的量子特征可用来侦测量子相变的发生。

由于氧化物高温超导材料的发现,量子海森堡模型备受关注,物理学家尝试用很多数值方法来研究它,如密度矩阵重整化群方法[4]、量子蒙特卡洛方法[5]等。海森堡自旋链[6,7]作为一种能够在固态系统中实现的理论模型,其研究方法和结果可为其他量子多体系统的研究提供依据,吸引了大量的关注并取得了很多进展,如利用量子无序(Quantum discord,QD)研究一维具有次近邻相互作用的自旋1/2 海森堡链的量子相变,利用自旋系统进行量子信息的传输[8]等。又因海森堡XXZ 自旋链模型能够很好地用来描述固体体系中比特之间的相互作用,经常用作量子纠缠及固体中各种量子相变机制的研究,如一维自旋1 键交替XXZ 链中的量子纠缠和临界指数研究[9]等。

以往研究中较多为海森堡模型的开链情况,本文对一维海森堡自旋开、闭链半填满(每个格点都填且只填一个电子)时不同位型[N,k](N 代表总格点数,k 代表格点中填放自旋方向朝上的电子数目,则剩余格点中填放自旋方向朝下的电子数目为N −k,k ≤N/2,以下同)的基态、激发态能量及磁矩情况进行研究,分析讨论了该系统的量子关联特性及量子相变情况,为深入了解海森堡模型量子关联特性提供参考信息。

2 理论模型及相关定义

2.1 一维海森堡自旋开、闭链模型概貌

Table 1 为一维海森堡自旋开、闭链模型的概貌,表中圆圈代表格点,↓、↓代表自旋向上或向下。格点是被对称单占据Halffilling(即半填满,自旋链每格点都填且只填一个电子,以下同)情况。

?

2.2 一维XXZ 海森堡自旋链模型的哈密顿量

一维XXZ 海森堡自旋链模型的哈密顿量为[10]

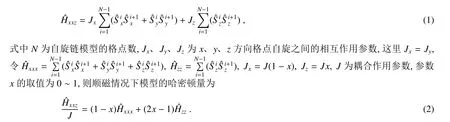
一维XXZ 海森堡自旋链模型的哈密顿量由XXX 和ZZ 模型的哈密顿量组合而成,开链时中i 值从1 取到N −1 即可。闭链时,需附加周期性边界条件,第i 与第i+N 格点位置的自旋与分别相等。

2.3 能量矩阵的构建及能量的获取方法

2.3.1 置换群产生完备基矢[11]

1)构建最原始基矢

2)求出置换群中的陪集

利用置换群算符描写一维海森堡体系的哈密顿量形式为

农村体育教师除了阅读教学专业杂志外，还应适当阅读核心体育科研杂志，如《体育科学》《中国体育科技》《体育与科学》《体育学刊》以及各个体育学院的学报等，这些核心期刊刊登的文章都是国内著名体育专家、教授、科研工作者的科研资料和多年的经验总结，通过阅读这些体育专业科研杂志，可使农村体育教师了解国内最新、最前沿的体育科研成果、信息和方向，开阔农村体育教师的视野，提升农村体育教师的素养。

4)完备基矢排序

把(w1, w2)中的(w1)部分看作是n 维矢量。如果(w1−)中最后一个非零分量小于0,就把(w1, w2)排在(,)之前,这时候,在排好序的基矢下相应的能量矩阵的矩阵元为w| ˆH/J|w〉, (w)是正规序列,(w)=(w1, w2)。

2.3.2 算符作用于完备基矢形成能量矩阵

2.3.3 获取能量

获取不同位型[N, k]、不同参数时一维XXZ 海森堡自旋链模型能量矩阵的本征值并排序,得到基态及不同激发态能量。

3 磁化强度

自旋链各格点中自旋用σ 表示,σ=±1,自旋向上为+1,自旋向下为−1, M =(∑σi)/N, M 为体系的平均磁化强度。

4 计算结果

Table 2 为一维XXZ 海森堡自旋开、闭链模型在参数x = 0.2,位型[5, 2]、······、[9, 4]时的基态能量(E);Table 3 为一维XXZ 海森堡自旋开、闭链模型位型[8,3]在参数x 从0.1 到1.0 时的基态能量(E);Table 4 为一维XXZ 海森堡自旋开、闭链模型在参数x=0.2,位型[6, 1]、······、[7,3]的第一、第二激发态与基态的能差(ΔE);Table 5 为一维XXZ 海森堡自旋闭链模型位型[5,2]在参数x 从0.1 到1.0时的第一、第二激发态的能差(ΔE);Table 6 为一维XXZ 海森堡自旋闭链模型位型[3, 1]、······、[8,3]时的平均磁化强度(M)。

限于篇幅,此处只罗列了部分数据结果的图表。

Table 2 Ground-state energy E of [5, 2],······,[9, 4]of XXZ Heisenberg model of the open and closed spin chain in one-dimension when x is 0.2

Table 3 Ground-state energy E of[8,3]of XXZ Heisenberg model of the open and closed spin chain in one-dimension when x ranges from 0.1 to 1.0

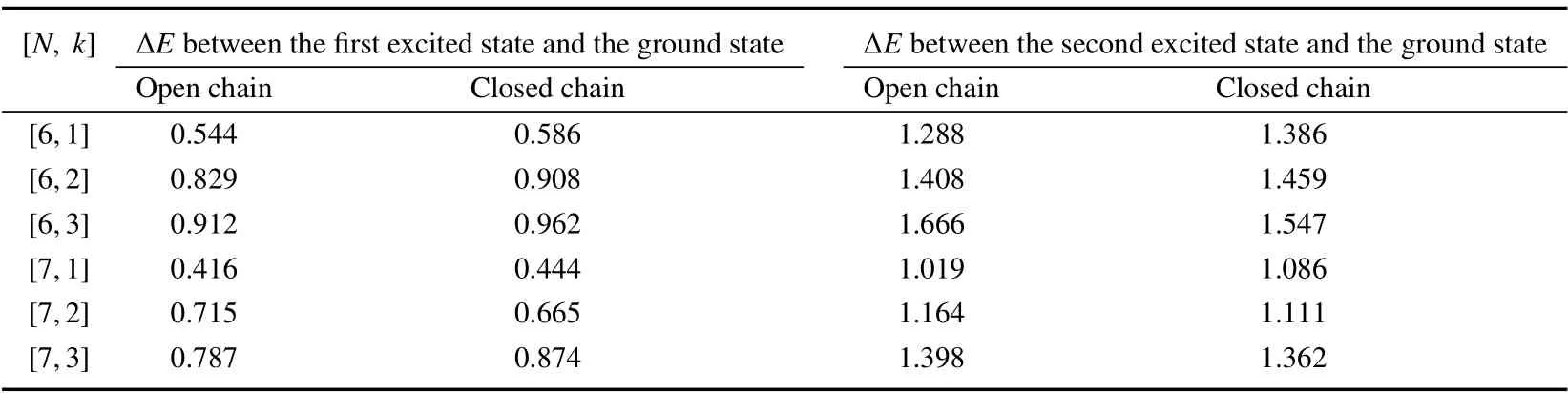
Table 4 Energy difference ΔE between the first,second excited state and ground state of[6, 1], ······ , [7, 3]of XXZ Heisenberg model of the open and closed spin chain in one-dimension when x is 0.2

Table 5 Energy difference ΔE between the first,second excited state and the ground state of[5,2],[6,2]of XXZ Heisenberg model of the open and closed spin chain in one-dimension when x ranges from 0.1 to 1.0

Table 6 Mean magnetization of[3,1],······,[8,3]of XXZ Heisenberg model of the open and closed spin chain in one-dimension

5 计算结果分析

5.1 能量分析

1)基态能量情况分析

Table 2 中参数x = 0.2 时, 位型[5,2]、[6,2]、[7,2] 开链相应的基态能量分别是−1.12、−0.889、−0.605,闭链相应的基态能量分别是−1.141、−0.959、−0.508,位型[7,2]、[7,3]开链时相应的基态能量分别是−0.605、−1.60,闭链时相应的基态能量分别是−0.508、−1.616。由此得出开、闭链情况下在x 和k 相同时,位型[N,k]的基态能量随N 增加而增加,而x 和N 相同时,位型[N,k]的基态能量随k 的增加而减小。系统的基态能量大,说明系统的基态结构不易改变,内在关联大;反之系统的基态能量小,系统的基态结构易改变,内在关联小。本模型中系统的基态能量情况很好地反映了系统的关联程度和系统改变的难易程度。Table 3 中,当x 从0.1 到0.9 时,位型[8,3]开链时相应的基态能量是−1.54、······、−1.08,闭链时相应的基态能量是−1.61、······、−0.99。当参数x = 1.0 时,开链时相应的基态能量从−1.08 降低到−1.25,闭链时相应的基态能量从−0.99 降低到−1.5,由此得出在开、闭链情况下,同位型[N,k]的基态能量随x(0 < x < 1.0)的增加而增加,在x = 1.0 处突然减小出现拐点,有突变。Fig.1、Fig.2 中可直观看出当x 从0.1 到1.0 时,开、闭链位型[4,2]、[6,3]、[8,4]的基态能量变化趋势先增加后减小,趋近x=1.0 时基态能量突然减小。量子多体体系中,多体系统的基态结构随着某些参量变化使系统发生突变的行为称为量子相变,量子相变是自发对称破缺的典型体现。在朗道理论中,当系统基态拥有的对称性变化时系统就发生了自发对称破缺,按临界点对称性思想,在相变临界区中可能存在新的对称性,本模型中系统的基态能量在x=1.0 的突变行为说明此处对称性发生了变化, x=1.0 是体系的相变点,此处体系发生相变。

Fig.1 E of[4,2],[6,3],[8,4]of the open spin chain versus x

Fig.2 E of[4,2],[6,3],[8,4]of the closed spin chain versus x

Fig.3 ΔE between the excited states and ground state of[6,2]of open spin chain versus x

Fig.4 ΔE between the excited states and ground state of[6,2]of closed spin chain versus x

2)激发态能量情况分析

Table 4 中,当x = 0.2 时:①开链位型[6,1]、[6,2]、[6,3]相应的第一激发态与各自基态能差ΔE 分别是0.544、0.829、0.912,闭链位型[6,1]、[6,2]、[6,3]相应的第一激发态与各自基态能差ΔE 分别是0.586、0.908、0.962;开链时相应的第二激发态与各自基态能差ΔE 分别是1.288、1.408、1.666,闭链时相应的第二激发态与各自基态能差ΔE 分别是1.386、1.459、1.547。②位型[6,1]、[7,1]开链时相应第一激发态与各自的基态能差ΔE 分别是0.544、0.416,闭链时相应第一激发态与各自的基态能差ΔE 分别是0.586、0.444;开链时相应第二激发态与各自的基态能差ΔE 分别是1.288、1.019,闭链时相应第二激发态与各自的基态能差ΔE 分别是1.386、1.086。由此得出在开、闭链情况下,当x、N 相同而k 增加时,位型[N,k]的第一、二激发态与各自基态能差ΔE 越来越大,说明系统的关联度增强,难以激发;而当x、k 相同而N 增加时,系统第一、二激发态与基态能差值ΔE 减小,说明系统的关联度变弱,较易激发。x、N、k 变化时的能量变化行为反映了系统改变难易程度、激发难易程度,很好地体现了系统的关联度。

Table 5 中,当x 从0.1 到1.0 时,开、闭链位型[5,2]相应的的第一激发态与各自基态能差ΔE 分别是1.12、1.02、······、0.5 和1.287、1.15、······、0,开、闭链位型[5,2]相应的第二激发态与各自基态能差ΔE 分别是1.95、1.75、······、0.5 和1.88、1.72、······、0。由此得出在开、闭链时随着参数x(0< x <1.0)增加,[N,k]的第一、第二激发态与基态能差ΔE 都呈减小趋势,参数x = 1.0 时有能级简并;从Fig.3、Fig.4 又可直观看出参数x 从0.1 到1.0 时,开、闭链时位型[5,2]、[6,2]的第一、第二激发态与各自基态能差ΔE 随x 增加而减小,参数x=1.0 时,降至最低并出现能级简并。量子力学中,能级简并是指一个能量值对应多个本征态,它是动力学对称性哈密顿量的一种集体表现,哈密顿量是表征体系特征的,体系的简并度与哈密顿量的某种对称性有关,简并度越大,对称性越高。一般来说,一个对称性往往对应一系列特定的能级简并,可通过寻找能级简并系列的方法来考察潜在的对称性,能级简并表明在临界区中存在着潜在的临界区对称性。Table 5 中参数x=1.0 时能级有简并,出现了临界区的对称性,按临界点对称性思想,在相变临界区中存在新的对称性,说明此处体系发生相变,x=1.0 是体系的相变点。

综上分析得出,开、闭链情况下, x、N、k 变化时能量的变化行为能很好地体现系统的关联度及相变情况。

5.2 磁化强度分析

磁化强度是单位体积内磁矩的矢量和,是在无外力场作用下,温度低于某一温度时,其内部原子磁矩自发有序排列的现象。自发磁化强度M 能描述系统的有序程度,可视作序参量。系统自旋取向的对称性被破坏时出现自发对称性破缺。磁矩取向较杂乱时M 较小,系统的对称性较高而有序度较低,若磁矩间交换相互作用使磁矩排列趋于平行,出现某一方向上的M,系统的有序度升高而空间对称性突然降低。相变是一种内部微观结构的有序和无序之间斗争的宏观外在表现,材料体系内部分子和原子之间的相互作用导致有序,热运动会引起无序和混乱。系统的无序会随着温度降低而降低,当一种相互作用的能量和热运动相比拟时,物质的状态会发生突变。当热运动的能量不足以破坏系统内部由于相互作用造成的有序,就发生相变现象。海森堡模型中对于磁性有贡献的电子被局域在原子范围内形成一个固有磁矩的模型,电子与电子之间的交换作用导致了自发磁化的产生。

Table 6 中,海森堡开、闭自旋链模型中位型[3,1]、[4,1]、[5,1]相应的M 值分别为1、2、3,位型[4,1]、[4,2]相应的M 值分别为2、0,可看出开、闭链时,k 相同,位型[N,k]的M 值随N 增加而增大,磁矩有序性增强,系统的对称性降低而有序度变高,磁矩间交换相互作用,使磁矩排列趋于平行,使得宏观总磁矩表现不为零,关联度增大;N 相同,位型[N,k]的M 值随k 的增加而减小,M 减小,磁矩取向趋向于杂乱,系统的对称性变高而有序度变低,关联长度变小,自发磁化用自旋波理论解释能反映有限晶格系统自旋能隙的存在。位型[N,k]中M 值随N、k 的变化规律为M = N −2k, [N,N/2]的M 值为0,对称性最好,有序性最低,本模型中M 很好地体现了海森堡开、闭自旋链的自旋排列、系统的对称性和有序度情况。利用海森堡模型自旋链模型, M 作为序参量来描述磁性物质的有序程度,为揭示铁磁性自发磁化的本质提供参考。

6 结 论

使用一维XXZ 海森堡自旋开、闭链模型在半填满、不同参数、不同位型[N,k](k ≤N/2)时的基态、激发态能量及平均磁化强度分析了系统的关联度及相变情况。当参数x、自旋链总格点数N、格点自旋方向朝上的电子数k 变化时的能量变化行为很好地体现了系统的关联度情况,由基态能量随x 变化时出现的拐点、激发态与基态能差ΔE 随x 变化时出现的简并情况找出体系的相变点。利用磁化强度M 作为序参量来描述磁性物质的有序程度, M 的计算结果很好地说明了物质的相结构发生变化时的序程度。开、闭链所做计算结果大体相同,闭链相比开链模型的计算效果要更直观、明显。总的来说,使用一维XXZ 海森堡自旋开、闭链模型的能量和平均磁化强度计算情况很好地反映了该体系的关联度及相变情况,为深入了解海森堡模型量子关联特性提供了一定参考。