忆阻器多涡卷混沌系统及其滑模控制同步

李晓霞, 冯志新, 张启宇, 王雪

(1 河北工业大学省部共建电工装备可靠性与智能化国家重点实验室, 天津 300130;2 河北工业大学河北省电磁场与电器可靠性重点实验室, 天津 300130)

1 引 言

作为第四种基本的双端电路器件,1971 年Chua[1]在理论上预测的忆阻器以其独特的性质而具有极大的应用价值。2008 年惠普实验室成功开发出忆阻器的实物,掀起了研究者们探索忆阻器的热潮[2～4]。忆阻器具有非线性的特性,将其引入电路后更容易产生混沌现象进而形成混沌系统。混沌系统在安全通信[5～7]、图片加密[8～11]等领域应用广泛,因此,构建具有多样性的混沌系统,使其在应用到保密领域后更难以被破解具有极大的研究意义,而忆阻器的引入为混沌系统的构建提供了新的思路。所以,人们采用各种方法构建忆阻混沌系统,并对其进行了深入的研究。Yang 等[12]提出了一种分数阶广义忆阻器,并用这种忆阻器替代传统的蔡氏二极管,得到了一种基于分数阶忆阻器的混沌电路。Bao 等[13]用忆阻器替代一个三维混沌电路的耦合电阻,形成了一种具有无限多隐藏吸引子的超混沌系统。Wang 等[14]利用三个忆阻器设计了一个六阶混沌电路,观察到了不同的吸引子相图,并研究了各忆阻器能量信号之间产生吸引子的情况。

同步现象广泛存在于物理、化学、生物等各个领域[15～18]。混沌系统之间的同步现象更是人们研究的热点。从完全同步[19]、广义同步[20]到组合同步[21]、准投影同步[22],人们在混沌同步方向取得了丰硕的成果[23～27]。但是,以前研究者主要关心系统之间是否能实现同步,而很少关注同步的速度是否可以更快,抗干扰的能力是否可以更强。

基于以上问题,本文将反映忆阻器性质的项及其他非线性项引入Yang 系统[28],提出了一个具有丰富多样性的混沌系统。改变系统的参数和状态变量的初始值可以得到单涡卷、双涡卷和三涡卷的混沌吸引子。然后以三涡卷时的系统为例,通过系统对初始值的敏感性、时域谱、功率谱、Poincare 截面、Lyapunov 指数和维数分析了系统的动力学特性,证实了该系统的混沌特性。接下来研究了忆阻混沌系统与加入了干扰信号的Chen 系统[29]的同步,利用滑模控制方法动态响应快、对外界干扰和模型的不确定性敏感度低的特点,设计了滑模控制器及参数自适应律。应用Lyapunov 稳定性理论得出了实现同步的充分条件。最后将该同步方法与没有使用滑模控制方法设计的控制器进行比较,结果显示该方法具有更快的同步速度和更强的抗干扰能力。

2 忆阻混沌系统模型

Yang 系统[28]可以描述为

式中x=(x1,x2,x3)T∈R3为状态向量,当α=35、β=3、γ=35 并且x1、x2、x3的初始值分别取1.15、3.5、3.3 时该系统处于混沌状态。然后,在描述Yang 系统的三个微分方程中各增加一项,得到忆阻混沌系统

式中x=(x1,x2,x3)T∈R3为系统的状态变量,a、b、c、d、g、h、m 为系统的参数, f(·)为系统中反映忆阻性质的函数,此处选用Bao 等[30]提出的光滑忆阻器模型,此模型具有三次单调上升的非线性特性曲线,其电荷与磁通的关系可以描述为

式中α′>0、β′>0 为忆阻器系统的参数,则它的忆导为

当α′= β′= 1 时,(3)式描述的是一个归一化磁控忆阻器。令系统(2)中的f(·)满足(3)式的形式,并令α′=β′=1,得

式中x3表示向忆阻器中输入的磁通, f(x3)表示忆阻器积累的电荷。将(5)式代入系统(2)中,选取系统(2)的参数为a = 16.5、b = 5、c = 15、d = 4、g = 10、h = 7、m = 6,且选取初始值为x1(0) = 1.74、x2(0) = 2.88、x3(0) = 0.8,利用四阶龙格库塔算法,仿真时间设置为300 s,可得到如Fig.1(a)的单涡卷吸引子。此外,选取系统(2)的参数为a = 17、b = 9、c = 15、d = 7、g = 10、h = 7、m = 0,初始值为x1(0)=1.7、x2(0)=1.9、x3(0)=1.5 时可得到双涡卷混沌吸引子,如Fig.1(b)所示。当系统(2)的参数为a=17、 b= 9、c=15、d = 7、g=10、h=7、m=6 且初始值为x1(0)=1.7、x2(0)=1.9、x3(0)=1.5时可得到三涡卷混沌吸引子,如Fig.1(c)所示。下面以三涡卷吸引子时的系统为例,讨论忆阻混沌系统的性质。

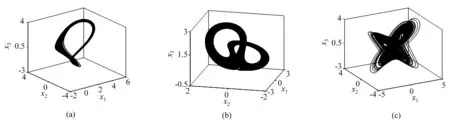
Fig.1 (a)Single-scroll attractor;(b)Double-scroll attractor;(c)Triple-scroll attractor

3 忆阻混沌系统的动力学特性分析

3.1 系统的初值敏感性及时域图分析

对初始值的高度敏感性是混沌系统的重要特征。对于同一个混沌系统，从两个极其相近的初始值出发进行演化，两组状态变量的值在短时间内相差不大,但是随着时间的推移必然呈现出显著的差异。Fig.2(a)反映了初始值相差10−8时忆阻系统的状态变量随着系统的演化而呈现出的差异,其中实线的初始值取值为(1.7,1.9,1.5),虚线的初始值取值为(1.7,1.9,1.5+10−8)。由图可见,开始时两个变量的波形重合,但随着系统的演化,两个波形的差异越来越大,最后成为完全不同的波形。说明该忆阻系统对初值有高度敏感性,符合混沌系统的特征。

Fig.2 (a)Initial value sensitivity verification;(b)Time domain waveform

系统(2)的x1时域波形如Fig.2(b)所示,系统呈现出一种类似随机的状态,而该系统方程的参数都是已确定的,不存在随机因素,由此可以判断系统确实存在混沌行为。

3.2 系统的功率谱及Poincare 截面分析

功率谱方法的基本思想是将动力系统的运动展成傅氏级数或傅氏积分,利用展开式的系数给出各频率成分的相对强度,分析频谱的相对强度的分布可以确定运动的特征[31]。系统(2)的功率谱如Fig.3(a)所示,该系统的功率谱是呈现噪声背景的宽峰连续谱,这是由于混沌运动具有内在的随机性特征。并且由于倍周期分叉,功率谱中还出现了许多峰值谱线。这些现象符合混沌系统功率谱的特征,说明系统(2)是一个混沌系统。

Poincare 截面又称Poincare 映射,其原理是从三维或高维连续系统到Poincare 截面上离散系统的映射,通过该方法,可以将动力系统的轨道转换成轨道与一个截面的交点来进行研究,从而可以在Poincare截面上观察系统形态随着时间的演化情况。当Poincare 截面上的图形是一段连续曲线或是具有分形结构的密集点时,可判定系统处于混沌状态。系统(2)中,x2=0 时的Poincare 截面如Fig.3(b)所示,符合混沌系统的特征,可判定系统(2)是一个混沌系统。

3.3 系统的Lyapunov 指数和维数

Lyapunov 指数是判断非线性系统是否存在混沌现象的重要依据。忆阻系统(2)的Lyapunov 指数谱如Fig.3(c)所示。三个Lyapunov 指数为L1=2.19、L2=0.014、L3=−16.75,并且L1+L2+L3<0。其中L1> 0 表示在该方向上相邻轨道迅速分离,系统的初始条件对系统长时间的演化有影响,即系统是初始值敏感的,运动呈现混沌状态;L2趋于0,对应稳定状态,初始误差不放大也不缩小;L3< 0 表示系统在该方向上相体积收缩,在整体上是稳定的。忆阻系统的Lyapunov 维数为2.13,出现了分数维,具有复杂的分形结构,符合混沌系统的特征,说明系统(2)是一个混沌系统。

4 混沌系统的广义同步

4.1 忆阻混沌系统与Chen 系统的滑模控制广义同步

选取忆阻系统(2)为驱动系统,将(5)式代入(2)式,并将(2)式的右端展开整理,令其参数的下标为1,可以得到

为便于说明,令q1=d1+1。

将加入了外界扰动和控制器的Chen 系统[29]作为响应系统,参数的下标为2,则

式中u1、u2、u3为广义同步的控制器,r1(t)、r2(t)、r3(t)为外界扰动,是不受状态变量约束的自由项,但为有界量,即|ri(t)|≤ηi, i=1,2,3,ηi>0 为常数。

定义广义同步的误差为

式中e=(e1,e2,e3)T, x=(x1,x2,x3)T, y=(y1,y2,y3)T,Φ(x)为广义同步映射函数,对(8)式求导可得

式中D 为雅各比矩阵算子,即DΦ(x)为Φ(x)的雅各比矩阵,二者选取如下

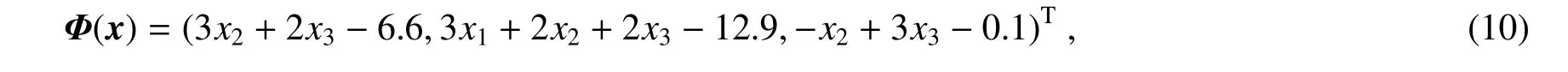
则其雅各比矩阵为

将(6)、(7)、(11)式代入(9)式得

选取滑模控制的滑模面为

式中s=(s1,s2,s3)T, λ=diag(λ1,λ2,λ3),且λ1,λ2,λ3均为大于0 的常数。广义同步的控制器为

将(14)式代入(12)式得参数自适应律为

选(13)式为滑模控制的滑模面,(14)式为控制器,(16)、(17)式为参数自适应律,则有如下定理成立。

定理:对于误差系统(15),如果满足k > ηi(i = 1,2,3),则广义同步误差e 沿着滑模面s 渐近趋于0,即驱动系统与响应系统实现广义同步。证明: 选取Lyapunov 函数为

当ηi−k<0,即k>ηi, i=1,2,3 时V˙ ≤0。根据Lyapunov 稳定性定理,误差系统e 的零解是渐近稳定的,即‖e(t)‖=0,驱动系统(6)与响应系统(7)实现广义同步。

数值仿真中选择滑模控制的滑模面为s=(4.5e1,1.5e2,5.5e3)T,即λ1=4.5,λ2=1.5,λ3=5.5。外部干扰信号是独立于状态变量的有界信号,不妨选择三角函数信号,即

驱动系统选用三涡卷混沌吸引子系统的参数和初值, 即a1= 17、b1= 9、c1= 15、q1= 8 (d1=7)、g1= 10、h1= 7、m1= 6, 这些参数为待估计的“未知”参数, 系统状态变量的初值(x1,x2,x3) =(1.7,1.9,1.5)。响应系统为Chen 系统,参数为a2=35、b2=3、c2=28,且状态变量的初值为(y1,y2,y3)=(1,−2,2), 其中a2、b2、c2也是“未知”参数。待估计的“未知”参数的初始值为:(0) = 14、(0) = 7、(0) = 16、ˆq1(0) = 7、(0) = 10、(0) = 9、(0) = 8、(0) = 38、(0) = 4、(0) = 24 且k=2.3>η1=η2=η3=0.5,满足定理中的条件。则可以得到广义同步误差随时间的演化曲线如Fig.4(a)所示,“未知”参数的估计值随时间的演化如Fig.4(b)～(d)所示。可以看出误差系统迅速趋于0,参数的估计值趋于其真实值。由于q1=d1+1,所以d1的估计值是7。

Fig.4 (a)Evolution of e with time. Estimation of(b)a1,b1,c1,(c)q1,g1,h1,m1 and(d)a2,b2,c2

4.2 同步的速度及抗干扰能力

同步控制器是实现混沌同步的重要因素。其设计的优劣直接影响混沌同步能否实现以及同步质量的好坏。同步的质量包含着对同步的各种要求,例如达到同步状态的速度以及同步的状态对外界干扰信号的抵抗能力。达到同步状态的速度可以通过同步误差e 趋于0 的时间长短来衡量,而同步的抗干扰能力可以通过观察同步误差e 趋于0 后加入干扰信号是否产生振荡来衡量。在本部分中,将加入了滑模控制方法的控制器与没有加入滑模控制的控制器进行比较,研究了当不加入干扰信号和加入由三角函数定义的干扰信号这两种情况下两个控制器对同步质量的影响。

前面已经介绍了滑模控制广义同步的控制器,下面给出当不采用滑模控制时忆阻混沌系统与Chen系统之间实现广义同步的各种必要参数以方便比较。

广义同步的误差为

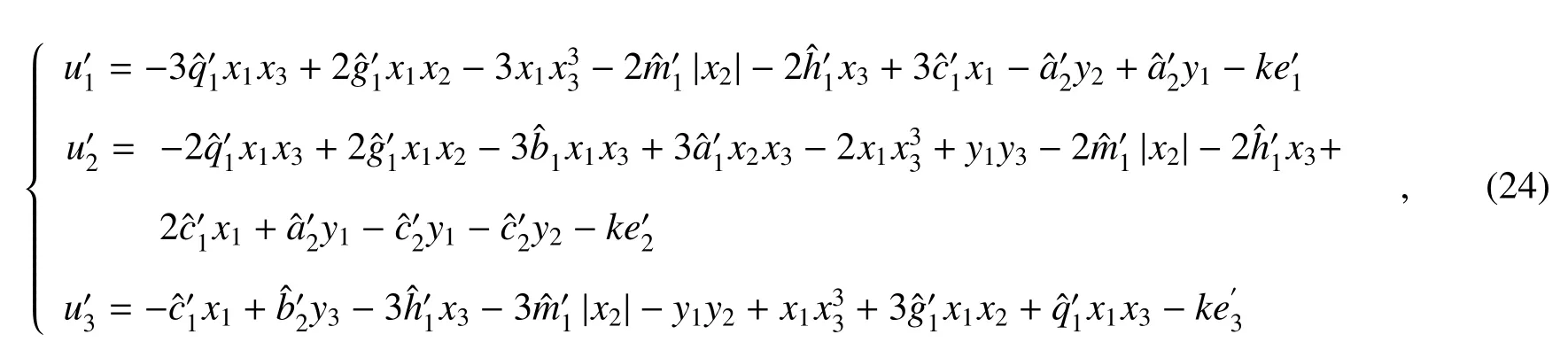
参数自适应律为

当不加入外界干扰信号,即(r1(t),r2(t),r3(t))T=(0,0,0)T时,若同步所需要的参数与上文中加入了滑模控制方法的对应参数选择相同的值,则此时未加入滑模控制方法的广义同步误差e′随时间的演化如Fig.5(a)所示。去除干扰信号后带有滑模控制的同步误差e 如Fig.5(b)所示。在Fig.5(a)中, e′大约13 s 时结束大幅度的振荡而趋于0,但在20 s 附近仍有小幅度的振荡。Fig.5(b)中,误差e 在5 s 时就结束大幅度振荡,并且没有再出现振荡,说明在两个控制器下忆阻系统与Chen 系统均能达到广义同步的状态,且滑模控制方法可以缩短误差趋于0 的时间,即提高了同步的速度。

Fig.5 (a)Synchronization error e′ without sliding mode control;(b)Synchronization error e with sliding mode control

当加入(22)式定义的三角函数干扰信号时,对应的参数值仍选择上述的参数值,则没有加入滑模控制方法的e′随时间的演化如Fig.6 所示,加入了滑模控制方法的e 随时间的演化已经在Fig.4(a)中给出。对比两图可知,没有加入滑模控制的情况下e′已经出现了振荡而无法趋于0,即两个系统在外界的干扰信号作用下无法维持同步状态,而加入滑模控制方法后两个系统仍能达到同步,说明滑模控制方法可以增强同步的抗干扰能力。

Fig.6 Synchronization error e′ without sliding mode control under the disturbance of trigonometric function signal

5 结 论

通过在Yang 系统中添加反映忆阻器性质的项和其他的非线性项,提出了一个忆阻混沌系统。改变系统参数的取值以及状态变量的初始值,得到了单涡卷、双涡卷和三涡卷的混沌吸引子。通过分析呈现三涡卷吸引子时系统的动力学特征,验证了其混沌的特性。基于Lyapunov 稳定性理论,应用滑模控制方法,设计了同步的控制器和参数自适应律,实现了所提出的混沌系统与加入了外界扰动的Chen 系统的广义同步。最后将应用与未应用滑模控制方法得到的同步误差进行了比较。仿真结果表明两个系统实现了同步,参数得到了准确估计,滑模控制方法使同步速度更快且抗干扰能力更强。