单镜面附近激发态极化原子的自发辐射

唐文涛

（荆楚理工学院，荆门448000）

1 引 言

It is well-known that the lifetime of excited atoms（or molecules）is determined by their spontaneous emission rate，which originates from the interplay of them and the zero-point fluctuation of radiation field such that can enhance or reduce the SE rate by changing environment conditions［1］.The effective control of atomic SE processes would play a critical role in many physics branches and have recently aroused great interest in connection with attempts to achieve amplification of quantum optoelectronic devices such as the solar cell，semiconductor laser，photodiode，single photon source，even quantum information processing.Up to now，the decay properties of atoms and molecules in thin films［2，3］，in photonic crystals［4，5］have been extensively studied.By means of the quantum electrodynamics（QED），Urbach and Rikken calculated spontaneous emission of atoms embedded in the nonabsorbing dielectric film［2］.The numerical results they got were accorded with the experimental results well.With photon closed-orbit theory（COT），Wang Fu-he，Wang Shu-bao and Jia Zheng-mao had investigated the spontaneous emission rate of atoms near an dielectric interface，inside a dielectric slab and near a perfect reflecting mirror［6-8］.Compared with the early work done by Bjork and Yamamoto which studied a thin quantum well sheet enclosed by a one-dimensional dielectric microcavity，Wangs and Du used quantum electrodynamics（QED）formulas to calculate the spontaneous emission rate.They found the frequencies of the oscillation calculated using QED matched very well with the prediction from closed-orbit theory，which suggested the photon closed-orbit theory is correct.Recently，Yun-Song Zhou et al.studied the switching control effects of SE by polarized atoms in two-dimensional photonic crystal.They found it was the orientation of the atomic dipole moment rather than pseudo photonic band gaps（PBG）can significantly bring about the switching effect between the inhibition and enhancement of the atomic SE and the decay lifetime may be enhanced to 33times［9］.In this paper，the spontaneous emission rate of polarized atom in the vicinity of a perfect reflecting mirror is calculated using Fermi's golden rule and semi-infinite response Green function approach.Scaling variables and Fourier transformations，which are standard tools of closed-orbit theory（COT）created by Delos and Du［10，11］，are used when we analyze the oscillations in the emission rate as a function of atomic position.Different with the work finished by Jia［7］，we find the emission rates exhibit damping sine-like oscillations pattern which depend not only on the atomic position，but also on the polarized orientation of atomic dipole moments.

The schematic diagram of the system under consideration is shown in Fig.1.One semi-infinite nonabsorbing dielectric material with real refractive index nand a mirror form a single plane interface at z=0.The material is assumed to be nonmagnetic.At Cartesian coordinate system，the origin is located at the interface and the zaxis is perpendicular to the interface.A polarized atom is placed at z point near the interface，its polarization direction can be turned in the xzplane，andθ represents the inclined angle between the atomic polarization direction and the xdirection.The y coordinate can be ignorable because the structure possesses translation invariance along the ydirection and symmetry of up and down reversion about the zaxis.We only need to talk about our questions under this two-dimensional system in this paper.According to Fermi's golden rule，the spontaneous emission rate of excited atom can be written as

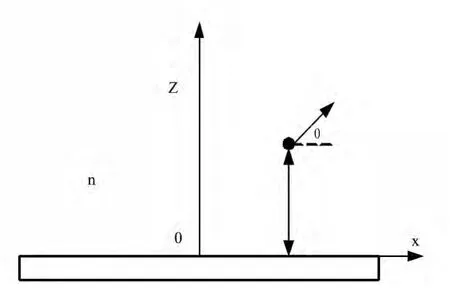
Fig.1 The schematic of the spontaneous emission of polarized atom in vacuum near a single mirror plane.The black dot denotes the atom.

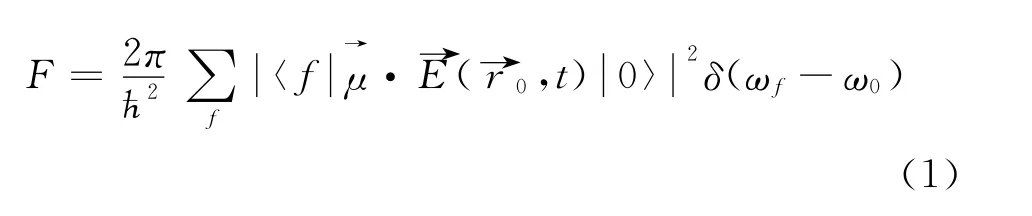
where the positive and negative frequency parts are the photon annihition and creation operators.Substitution of Eq.（2）into Eq.（1）yields

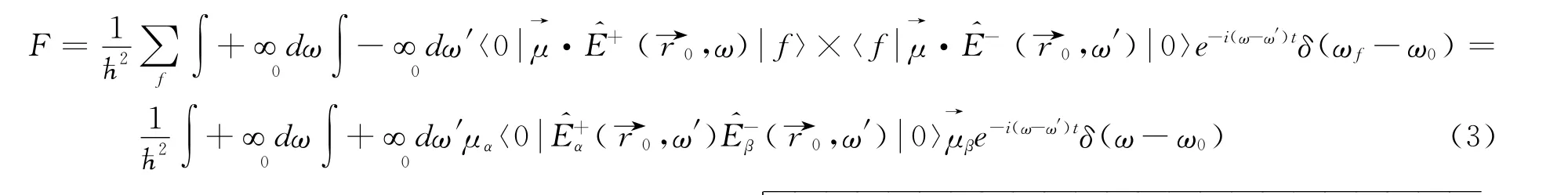
Taking advantage of the gauge in which the scalar potential vanishes，that is

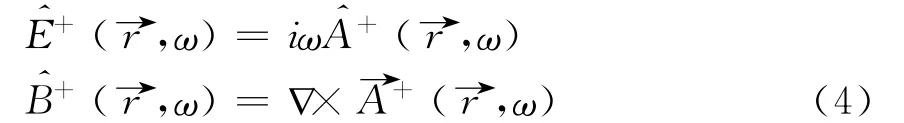
the electric field correlation function is related to the imaginary part of the vector potential Green function by using the fluctuation dispersion theorem and the Kubo's formula

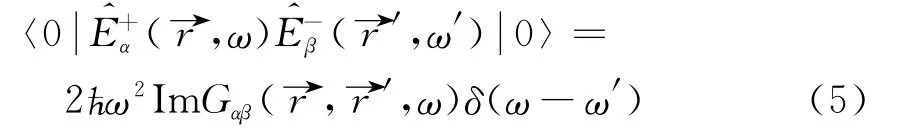
Employing Eq.（5）and pay attention to=，expression（3）can be reduced as

The explicit form of the coordinate space Green function in this configuration can be written as

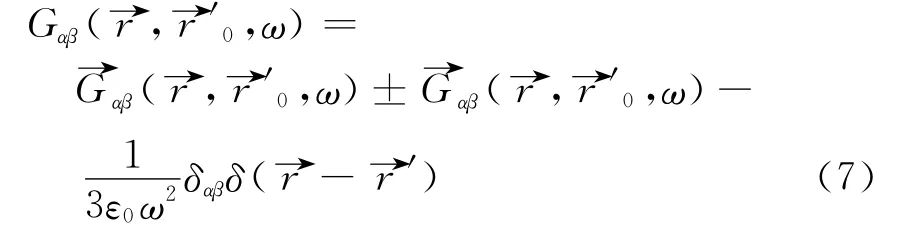
where the plus sign holds forαβ=xz，yz，zz and the minus sign holds for the other components.The tensor→Gαβ（→r，⇀r′i，ω）is given by［12］

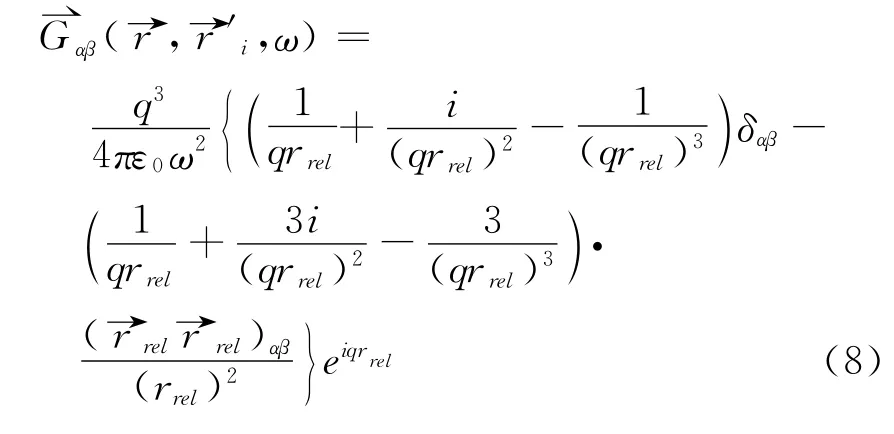
where→rrel→rrelis the normal Cartesian dyadic and

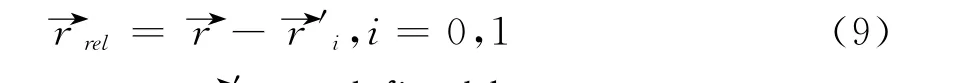
The vectors→r′iare defined by

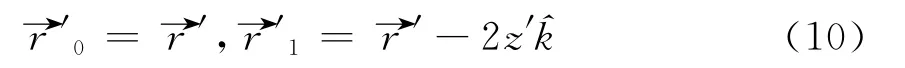
Substitution of Eqs.（7～10）into Eq.（6），we have

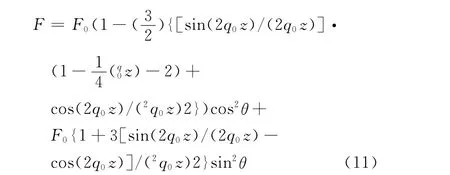
where q0=ω0／c，zis the position of the emitting atom，F0is the decay rate of the polarized atom in free space

whereε0is the permittivity of vacuum，cis the velocity of light.

We first calculate the spontaneous emission rate F of atom polarized in several given directions，for instance，θ=0°，30°，60°，90°.In order to describe the properties of the decay rate conveniently，we introduce a scaling variableαto measure the distance of the atom to the interface，that's z=αd0，where d0=λ0=510nm is a typical size of the system.In Fig.2（a～d）theFis plotted as a function ofαwith a step sizeΔα=0.05for different polarizationθ=0°，30°，60°，and 90°，respectively.All curves show damping sinelike oscillations in these four figures.But as the increase of the angleθ，the oscillation becomes more decreased.Whenθ=0°，the atomic polarization is parallel to the mirror plane，the relative amplitude of the oscillation reaches quite large.Asθ=90°，the perpendicular case，corresponding to smaller oscillatory amplitude that almost is not visible as shown in Fig.2（d）.This reason can be explained exactly in the following of our paper by using the photon COT.

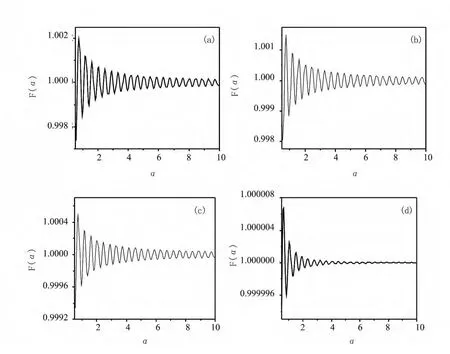
Fig.2 The spontaneous emission rate（relative to the value invacuum）as a function of the atomic relative positionα=d／d0for different polarized directions（a）θ=0°，（b）θ=30°，（c）θ=60°，and（d）θ=90°，respectively

In order to extract the frequency in the damping sine-like oscillations of the spontaneous emission rate，we follow the standard approach in the COT，using modified Fourier transform（FT）defined by

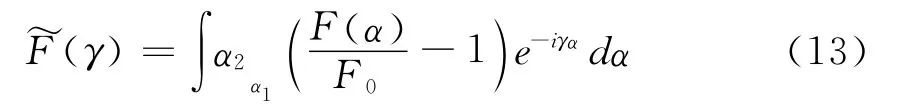
Fig.3（a～d）displays the absolute value of～F（γ）corresponding to the（SE）rate in Fig.2（a-d）.One can identify only a single peak at 12.62in each figure of Fig.3.But with the increase ofθ，the strength of the peak becomes gradually smaller，and whenθ=90°，the peak structure is al-most vanished，as seen in Fig.3（d）.In order to understand these properties，we extend electron closed（COT）to photon（COT）to analyze the oscillations in the spontaneous emission rate.According to COT，the formula of the spontaneous emission rate reads：

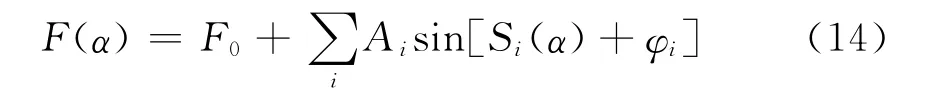
where F0represents a background term relating to the（SE）rate of vacuum case n=1.0.It associates with the direct emission process in which the emitted photon leaves the atom and never returns back to atom.The sum includes all permitted classical closed orbits of emitted photon going out from and returning back to the emitting atom；the emitted photon obeys the laws of speculum reflection at mirror plane and refraction when it travels in these closed trajectories；Si（α）=kLiis the action of the photon along the ith closed-orbit，kis the wave number，and Liis the geometric length of the closed orbit；the amplitude Aivaries slowly and is a measure of the intensity of the returning family of photon trajectories.The phase accumulations，including Maslov phase corrections，are denoted inφi.

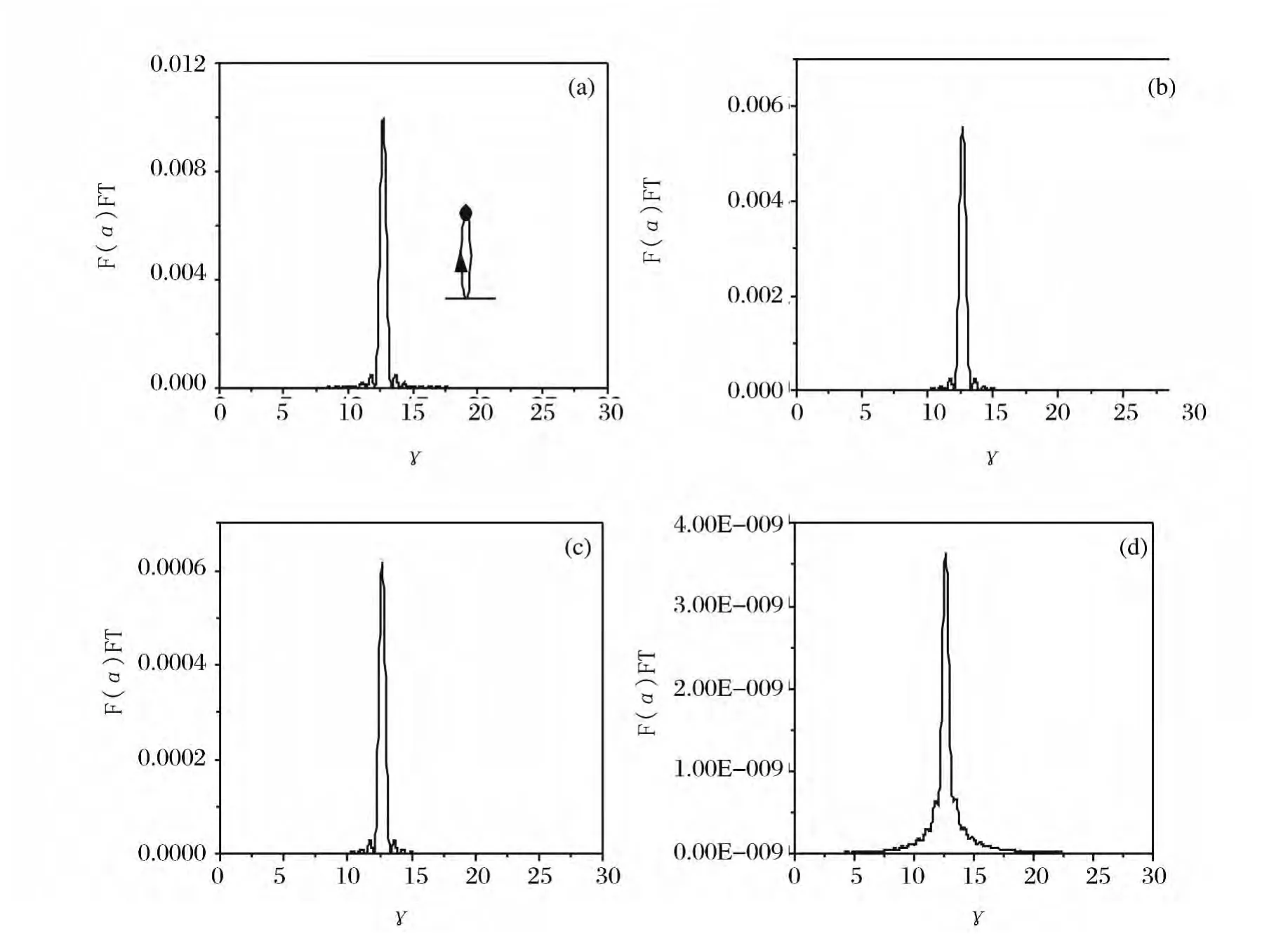
Fig.3 Fourier transform of the spontaneous emission rateF（α）in Fig.2for different polarized directions（a）θ=0°，（b）θ=30°，（c）θ=60°，and（d）θ=90°，respectively

Fourier transforms of Eq.（14）also gives peak position determined by the actions of emitted photon around closed orbits.BecauseSi=，when the system sizeα=1，=k0Liis the reduced action of the ith closed orbit.COT predicts the ith peak atin the Fourier transform.In the casen=1.0，COT gives the photon closed orbit at the position S0=（2π／λ0）（2λ0）=4π=12.57，agrees well with the numerical calculations by using Fermi's golden rule，semi-infinite response Green function and Fourier transform.

The physical image for the spontaneous emission process can be elucidated in the scheme of the photon（COT）as follows：when the polarized atom makes a transition from the excited state to a lower one，an electromagnetic wave representing the emitted photon is created near the atom.This photonic wave involving whose propagation can be approximated by semiclassical mechanics and related to outgoing classical trajectories，when a family of trajectories leaves away from the atom to a large distance and hit the mirror interface，some of the associated waves are returned back to the atom.The returning waves interfere with the outgoing electromagnetic wave to produce the visible oscillations in the spontaneous emission rate.

The oscillations in the spontaneous emission in Fig.2can be explained as quantum interference between emitted photon wave near the atom and the photon waves returning back to the atom.Each closed orbit makes an oscillatory contribution to the rate with a characteristic frequency determined by its action.Since the action of the photon closed orbit is irrelevant to the atomic polarization，therefore the peak position in each plot of Fig.3is the same.But with the increase of the angleθ，the rate of the photon waves returning back reduces，causes the decreasing of the oscillations in the emission rate.Whenθ=00，the atomic polarization parallel to the mirror plane，the relative height of the peak implies relative large returning back rate，such that results in the amplitude of the oscillation relative large.And whenθ=90°，the perpendicular case，the peak is almost vanished，very few photonic waves coming back to the atom to interfere with the emitted one，the oscillation in the decay rate almost is not visible，as seen in Figs.2（a，d）and 3（a，d）.

In conclusion，we have derived a formula for the（SE）rate of polarized atom in the vicinity of a mirror plane using Fermi's golden rule and Green function approach.The results show that the decay rate of the polarized atom displays damping sine-like oscillations around the real refractive index of the medium surrounding the atom，which depend on the scale parameter of the system，and are closely related to the distance of the atom to the mirror plane and the polarized direction of the atom.For present situation，the oscillation strength in the（SE）rate is decreased with the increase of the polarized angleθ.In the view of the closed-orbit theory，each closed photonic orbit produces a visible oscillation，and its oscillatory frequency can be extracted by Fourier transformation.The position spectrum of the peak agrees with the action of the emitted photon well.And the decreasing of the oscillation in the decay rate could be explained as the decreasing of the photon waves returning back.This study suggests that the atomic spontaneous emission process can be controlled effectively by changing the polarized orientation of the atom near a mirror plane.And it is a successful sample by using the closed-orbit theory to represent the oscillation in the spontaneous emission rate of atom in environments.

［1］ Jia Z M，Wang S B，Lin S L.Lifetime distribution of the spontaneous emission of atoms in a dieletric microcavity［J］.J.At.Mol.Phys.，2008，25（3）：607.

［2］ Urbach H P，Rikken G L J A.Spontaneous emission from a dielectric slab［J］.Phys.Rev.A，1998，57：3913.

［3］ Yablonovitch E，Gmitter T J，Bhat R.Inhibited and enhanced spontaneous emission rate from optically thin AlGaAs／GaAs double heterostructures［J］.Phy.Rev.Lett.，1988，61：2546.

［4］ Lenac Z.Spontaneous emission from a qusi-two-dimensional Winger crystal in a multilayer configuration［J］.Phys.Rew.A，2001，63：033815.

［5］ Wang X H，Kivshar Y S，Gu B Y.Giant lamb shift in photonic crystals［J］.Phys.Rev.Lett.，2004，93：073901.

［6］ Wang F H，Jin Y P，Gu B Y，et al.Application of closed-orbit theory to the spontaneous emission of atoms near a single dielectric interface［J］.Phys.Rev.A，2005，71：044901.

［7］ Du M L，Wang F H，Jin Y P，et al.Oscillations in the spontaneous emission rate of atoms in a dielectric slab：Effects of photon closed orbits［J］.Phys.Rev.A，2005，71：065401.

［8］ Jia Z M，Zhou-Hui，LIN Sheng-lu.Application of closed-orbit theory to the spontaneous emission of an atom in the vicinity of a mirror［J］.J.At.Mol.Phys.，2008，25（6）：1427.

［9］ Zhou Y S，Wang X H，Gu B Y，et al.Switching control of spontaneous emission by polarized atoms in two-dimensional photonic crystals［J］.Phys.Rev.Lett.，2006，96：103601.

［10］ Du M L，Delos J B.Effect of closed orbits on quantum spectra：Ionization of atoms in a magnetic field.I.physical picture and calculations［J］.Phys.Rev.Lett.，1988，38：1896.

［11］ Du M L，Delos J B.Effect of closed orbits on quantum spectra：Ionization of atoms in a magnetic field.Ⅱ.deviation of formulas［J］.Phys.Rev.Lett.，1988，38：1913.

［12］ Matloob R.Casimir effect between two conducting plates［J］.Phys.Rev.A，1999，60：3421.