输气管道第三方破坏数值分析及安全评价方法
2020-02-24黄雪松周兆明谭金松
黄雪松, 张 佳, 周兆明*, 谭金松
(1.中原油田分公司石油工程技术研究院,濮阳 457001;2.西南石油大学机电工程学院,成都 610500)
中国油气管道工程在近20a得到了快速发展,截至2015年底,在役油气管道总里程约15万km,油气长输管道总里程位列全球第三,其中天然气管道约7.7万km,占管道总里程的51.3%[1-3]。EGIG数据调查报道,输气管道事故的主要因素是第三方破坏(占总事故的50%)、腐蚀(占站事故的15%),材料缺陷(占总事故率的16%),其中,第三方破坏是造成管道失效的主要原因[4-5]。随着输气管道铺设距离的延长,管道面临的第三方破坏问题更加严重,且呈上升趋势,严重影响管道安全运行[6-8]。2010年美国德州、旧金山和2015年美国加州天然气管道因第三方挖掘作业时造成管道破坏,发生严重的爆炸事故。2013—2015年,中国先后在广西北海、安徽芜湖、山东青岛等地发生严重的第三方破坏管道事故,造成严重的人员死伤和经济损失。通常,第三方破坏后管道可能出现漏孔,气体从漏孔漏出;或管道未发生泄漏,管道只是局部出现屈曲、凹坑,若不及时更换,在连续服役之后管道凹坑可能会演变为更严重漏孔,导致管道出现泄漏。在外国,1992年,Muhlbauer编写的《管道风险管理手册》详细介绍了管道风险管理措施[9-10]。1999年,美国机械工程师协会开始实施标准ASMEB31.8《输气和配气管道系统》,经连续修正完善,形成了完整的管网完整性管理风险评价[11]。2002年,Brooker[12]针对负荷作用下的管道损伤情况进行了研究分析,应用有限元仿真软件ABAQUS研究挖掘机斗齿齿形、管径等参数对载荷的影响,并得出计算斗齿载荷方程。2004年,Brooker[13]研究了不同机械斗齿齿形的静态穿透力,验证了载荷方程可行性评价。Guerreiro等[14]介绍了一种用于估算膜应变有限元方法。并结合弯曲应变和膜应变,给出了缩进管内外表面的总应变场,使用不同分辨率的虚拟几何工具对管道凹痕进行了准确的安全评定。在中国,2011年和2015年,徐涛龙等[15]、周立国等[16]研究了管道第三方破坏成因、影响因素、风险评价方法及相应预防措施,取得了较大研究成果。景勇等[17]通过海底管道的凹坑缺陷实例,考虑二级评价和三级评价,得出该段海管的更换建议。徐尊平等[18]根据凹坑缺陷不同的分布状况,采用了不同的方法进行评定,结果表明其对应的评定点落在评定曲线定义的安全范围内[19]。张镇等[20]对不同地区天然气管线建立第三方破坏模型,对管道第三方破坏失效进行了定性研究分析,得出第三方破坏是引起管道失效的主要因素,并提出管道遭受破坏的预防措施。
中国管道更换修复措施虽取得较多进步,但存在较多知识不系统、技术不先进等问题。现通过数值仿真分析,对挖掘机斗齿作用管道过程及破损管段更换给出合理更换建议;提出适用于挖掘机斗齿作用下的破损管道修复更换的评价准测,并结合具体案例对管线进行安全性能分析。
1 管道第三方破坏更换理论
目前,国际上有两种管道更换依据:①管道表面凹坑深度超过6%的名义管径时需进行更换;②依据管道应变准则,以外表面凹坑最大应变的6%为标准更换破损管段。目前中外学者只对凹坑长度和深度做了相应分析,但都没考虑破损管段外表面凹坑形状及薄膜应变分量,结果不够精确。依据经典薄壳弹性基础理论,弯曲和薄膜应变作用下壳体模型发生的变形,采用薄壳弹性的基础理论公式计算,z曲面沿轴向和周向的应变如式(1)、式(2)[21-23]所示。
(1)
(2)
采用弧长法推导薄膜应变,基于最小二乘拟合的四阶B样条曲线拟合[24-25],薄壳轴向和周向薄膜应变如式(3)、式(4)所示。
(3)
(4)
式中:Lx为凹坑轴向弧长,mm;W(x)为凹坑轴向轮廓曲线方程;Ly为凹坑周向弧长,mm;W(y)为凹坑环向轮廓曲线方程。
依据Von Mises准则,推导出总等效应变εeq为。
(5)
式(5)中:εx为轴向应变;εy为环向应变;εz为轴向应变;v为泊松比,取v=0.5。
最大应变发生在凹坑最深处的内外表面,因此,总的等效应变如式(6)、式(7)所示。
(6)
(7)

从式(6)和式(7)可知,进行输气管道凹坑分析时,取管道凹坑最深处的外表面总等效应变的较大者与允许应变进行比较,当管道凹坑的最大应变大于等于许可应变时,说明该管段需进行更换和维修。
2 斗齿作用管道过程仿真研究
2.1 数值模型建立
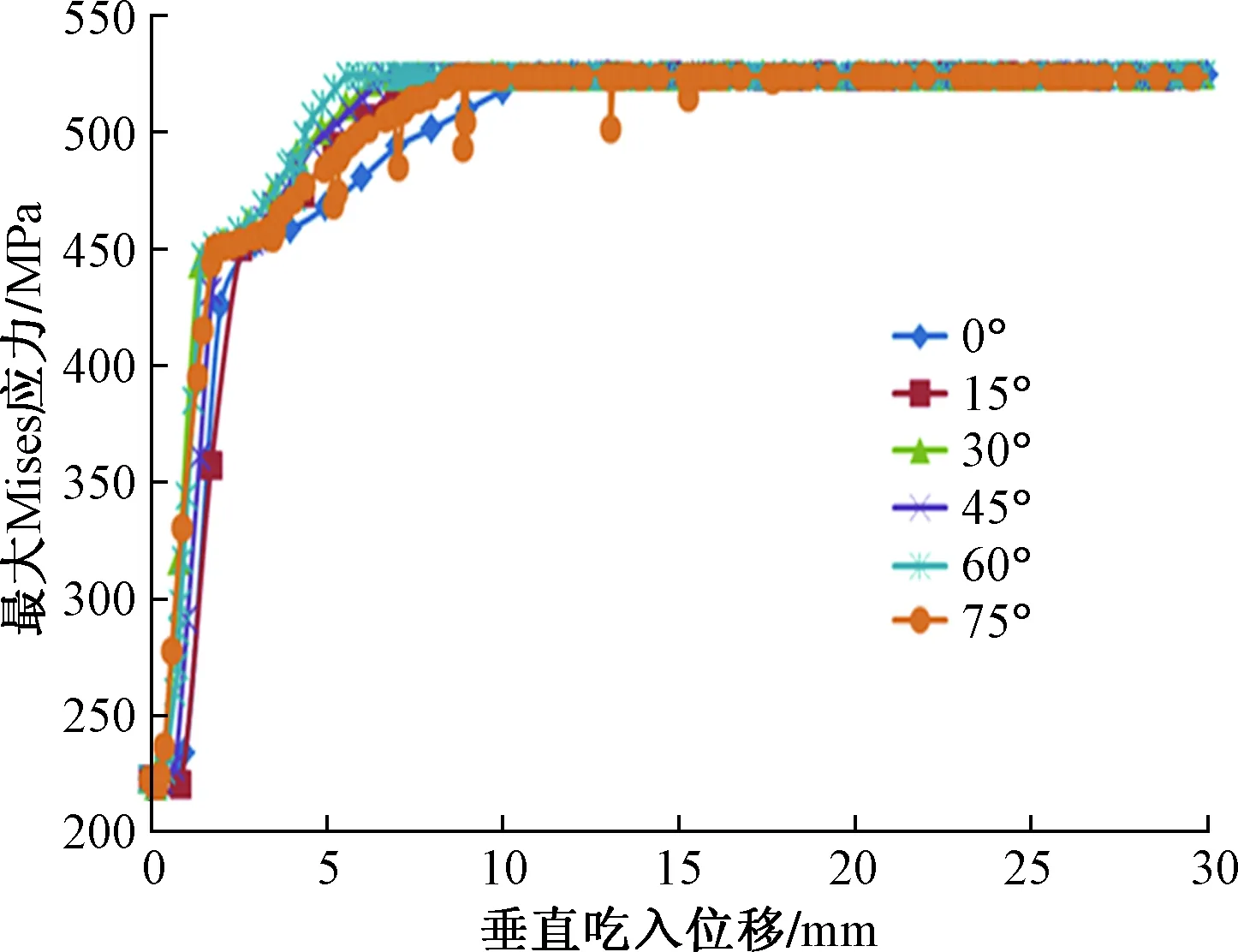
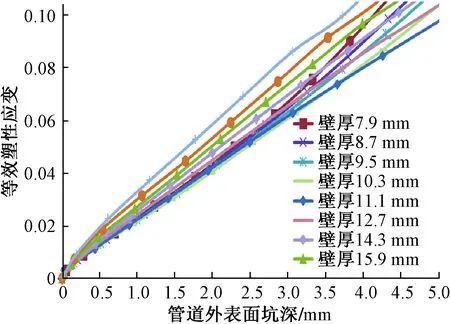
第三方挖掘机斗齿作业时通常是一个或者多个斗齿以随机角度、高度和速度冲击管道。由于斗齿之间的相互独立性,只分析单个斗齿冲击管道的过程。因斗齿与管道外表面随机接触,为简化模型,现设定作用点为管道顶部中央。此假设情况下,以管道遭受挖掘机破坏为研究对象,建立斗齿冲击管道有限元模型[26-28],如图1所示。斗齿与管道接触点与竖直方向夹角为α,吃入垂向位移为H。斗齿卸载后,管道形成的凹坑回弹,最终在停止输压情况下凹坑的最大深度d 图1 斗齿冲击管道有限元模型Fig.1 Finite element model of bucket impact pipe 挖掘机破坏管道过程分为四个阶段:①对管道加载正常输气内压;②斗齿以角度α、垂直深度H加载;③卸载斗齿载荷,管道回弹过程;④停止输气。假定正常管道输气过程中,管内压为4.7 MPa,管道应力约为180 MPa,远远低于管道屈服强度(450 MPa),说明正常输气时管道强度在安全范围内,仿真结果如图2所示。 图2 正常输气时L450管道应力Fig.2 L450 pipeline stress during normal gas transmission 斗齿与管道接触位置不同会使两者接触关系不同,影响管道的破坏程度和剩余寿命。建立不同的斗齿与管道接触角度,通过模拟分析可以看出,如图3所示,斗齿吃入深度H不变时,管道最大Mises应力与接触角度几乎无关,仅与吃入深度H相关。最大Mises应力小于450 MPa时,最大Mises应力与H呈线性关系。随着最大Mises应力增加,曲线表现出屈服特征;当超过525 MPa后,管道进入被破坏阶段。 图3 管道最大Mises应力、反作用力关系曲线(不同作用角度)Fig.3 Pipeline maximum Mises stress, reaction force curve (different action angle) 由2.2节分析可知,管道最大Mises应力仅与斗齿垂直吃入深度H有关,因此对α=0°时不同吃入深度(H=2.0、6.0、10.0、80.0 mm)的卸压过程进行仿真分析,分析结果如图4和图5所示。当斗齿冲击管道后停止输送管压,管道处于自由放置状态,无外力作用。从图4(a)可以看出,完全卸压后的管道,除局部区域外,其他管道外壁面基本处于无应力状态。但在斗齿与管道接触位置的外壁面上出现约172 MPa的残余应力。由于残余应力较小,可认为斗齿吃入深度H=2.0 mm作用下管道基本不受影响,仍可继续正常运行。从图4(b)中可以看出,斗齿与管道接触位置的内外壁面上出现最大Mises应力477 MPa,比斗齿加载过程中的最大Mises应力略大,此时需加强管道巡线力度。 从图4(c)可以看出,当吃入深度H=10.0 mm时,完全卸载管内压后,外壁面上出现约512 MPa的残余应力,残余应力区域扩大,残余应力远高于管道的屈服强度(450 MPa),因此需及时更换局部破损管道。 图4 卸载内压后云图Fig.4 Cloud image after unloading internal pressure 图5 管道破坏时云图Fig.5 Cloud image after unloading internal pressure 当斗齿吃入深度H=80.0 mm时,如图5所示,外壁面上平均残余应力远高于管道的屈服强度(450 MPa),斗齿已穿透管道内外壁面,卸掉斗齿后管道明显产生漏孔,且漏孔周围管壁变形较大。由此可知,管道发生了严重气体泄漏,需采取相应应急措施更换破损管段。综上分析,随斗齿冲击管道的吃入深度逐渐增大,管道内外壁面的变形更大,卸载内压后管道凹坑变形越明显,直至管道被冲击产生泄漏孔洞。 实际对管道凹坑进行讨论时,取管道内外表面(凹坑最深处)总等效应变与标准应变比较,当凹坑应变大于等于标准应变时,需进行管段的修复更换。工程现场除直接观察管道破损情况外,管道外壁面的凹坑深度d更易测量。通过数值分析,计算管道不同壁厚、凹坑深度与管道最大应力曲线关系,以此来判断管线是否需要更换,为现场快速准确判定提供理论依据。 对破损管道输气状态和停气后的最大应力与管道凹坑深度d进行效应分析,从图6、图7可知,管道最大应力发生在管道内表面,数值略微发生变化,差异不大。比较分析破损管道无论是否继续输气,当管道凹坑深度大于0.5 mm时,管内壁最大残余应力大于管道屈服强度,但最大Mises应力增加不明显,无法判断管段更换与否。 图6 运行情况下的Mises应力Fig.6 Mises stress in operation 图7 卸载内压后的残余应力Fig.7 Residual stress after unloading internal pressure 当发生第三方破坏后,无论管道是否停气,塑性应变都随凹坑深度d增大而增大,如图8、图9所示。随管壁厚度增加,相同凹坑深度的管道塑性应变依次增加;相同壁厚的管道,管道运行时的塑性应变比停气时更大。 图8 管线运行时的塑性应变Fig.8 Plastic strain during pipeline operation 图9 管道停输时的塑性应变Fig.9 Plastic strain when the pipeline is stopped 为提出合理更换管道的建议,现基于《气体传输与分配管道系统》评价准则,以管道凹坑应变的6%为临界值,判断管线更换与否,若超过6%的最大应变,建议更换破损管段。当破损管道仍运行时,需更换凹坑深度为2~2.5 mm的管段;停输后需更换的管段凹坑深度为2~3 mm。因此,管道表面凹坑深度低于2 mm时,不需要更换,但需定期巡检;凹坑深度处于2~3 mm时,依据管道壁厚确定是否需要管段的更换;当凹坑深度大于3 mm时,需要更换管道的凹坑部分。 图10为某管线(L450)施工现场图,依据现场施工过程中管线实测数据,对第三方挖掘机施工影响下的管线进行修复更换分析。 图10 挖掘机斗齿作用管道现场图Fig.10 Site picture of bucket tooth action pipeline of excavator 图11 管道残余应力云图Fig.11 Pipe residual stress cloud diagram 图11为管道残余应力云图,卸压后最大Mises应力约224 MPa(正常输气时L450管道应力约222 MPa),因此通过残余应力无法判断管段是否需要维修更换。通过对比分析该管段实测数据,开挖验证管道外表面凹坑深度为1.4 mm,破损程度较小,无需更换此管段,但作为高后果区需定期检测。案例分析结果与仿真结果一致,能为实际现场输气管道第三方破坏修复更换提供理论支持。 采用有限元分析软件,建立第三方挖掘机斗齿作用管道过程模型,对斗齿不同的冲击角度和深度对管段损伤程度进行系统研究,得出如下结论。 (1)挖掘机斗齿冲击管道时,管道外表面凹坑两边出现应力集中区,管道局部产生塑性。吃入管道深度H不变时,最大Mises应力、反作用力与作用角度基本无关,仅与吃入深度有关。 (2)斗齿作用深度越大,管道变形越大,卸载管压后凹坑变化越显著,凹坑越大。当吃入深度H=80.0 mm时,平均最大应力远大于管道屈服强度,斗齿已穿透管壁。 (3)当管道外表面出现凹坑时,管道内表面会发生相应形变,且残余应力较大。会大大降低管道局部负载能力,影响管线长期安全运行。 (4)参考《气体传输与分配管道系统》应变评价准则,提出以应变6%为临界值判断管道更换与否。当外表面凹坑深度小于2 mm,建议不更换,需要定期检测。凹坑深度处于2~3 mm时,依据管道壁厚确定是否需要管段的更换;当凹坑深度大于3 mm时,需要更换管道的凹坑部分。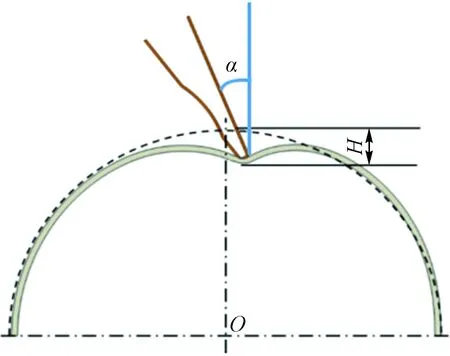

2.2 斗齿冲击角度对管道的影响
2.3 斗齿垂直吃入深度对管道的影响





3 案例分析


4 结论
