基于卡方检验的计算流体动力学网格无关性分析

谢 宇， 任金波， 黄煌辉， 张 翔

(福建农林大学机电工程学院,福州 350002)

计算流体动力学(computational fluid dynamics, CFD)[1],其技术取得了快速的发展[2-3],数值模拟方法的应用日趋广泛[4-7],所面对的问题越来越复杂,但数值模拟在不同工程环境下的表现值不一样[8],因此数值模拟的可靠性验证是判断数值模拟可信度的重要方面,计算结果可靠性分析方法主要有基准解比较法、实验比较法和网格收敛性分析法三种[9-13],网格收敛性分析法中最流行的是Roache[14]提出通过计算网格收敛指数(grid convergence index,GCI) 来评估数值误差的方法,现阶段GCI方法已广泛应用于数值计算误差,Craig等[15]利用GCI对厌氧消化器搅拌模型进行误差分析,Karimia等[16]分析了GCI 中的关键参数对旋液分离器数值误差的影响,郑秋亚等[17]针对M6机翼的绕流问题,就网格密度对 5 套不同网格的CFD模型进行了GCI分析, Longest等[18]使用GCI分析不同网格样式对于生物流动系统的流速场等因素的影响,刘厚林等[19]借助GCI对比分析了不同网格类型的离心泵内部流场情况,GCI方法在一定程度上提高模拟的准确性并提供理论支持,但仍存在以下不足:① GCI方法在网格以整数倍形式加密时计算结果可靠,但是在实际操作中(尤其是多维模型时)往往很难做到,同时若网格加密倍数过小,解的变化不明显；②在多维模型中,不同方向网格加密倍数可能不一样,须在每个方向先分别计算相应的 GCI,然后再迭加求其和,而在实际操作中很难做到；③截差阶数p较难确定；④渐近范围的判断没有绝对值,网格加密到一定程度时计算结果会进入到渐近收敛范围,再对网格进行加密没有太大的意义[20-21],因此,确定合适的渐进收敛范围很重要。

基于此，对刀片切泥制浆数值模拟进行CFD网格无关性的分析,探讨在混合网格下网格无关性的网格数量,在允许误差范围内借助卡方检验验证网格无关性,再与GCI方法进行对比,最终和试验结果来判断是否合理,探究适用于刀片切泥制浆模拟的网格无关性所对应的最优网格数,以分析在非整数加密以及加密方式不一致情况下的网格收敛分析准确性,以期为今后相关研究提供借鉴和启发。

1 模型与方法

1.1 物理模型

以刀片旋转切割泥浆来培浆的过程为研究对象,设计泥浆槽长宽高为2 000 mm×2 000 mm×1 600 mm,一侧有一台阶,刀片转速为40 rad/s,泥浆被旋转的刀片切割飞溅至一侧台阶上,来模拟现实中水稻田里泥浆被刀片旋转打到育秧盘的工作环境,其物理模型如图1所示。

图1 刀片切泥制浆模型简图Fig.1 Model diagram of blade cutting mud

1.2 建模及网格划分方法

用Pro/Engineer软件对模型进行建模,使用CFD前处理软件(the integrated computer engineering and manufacturing code for computational fluid dynamics, ICEMCFD)尽可能对结构模型采用结构化网格划分,网络模型的划分方法和网格质量对数值模拟结果具有极大影响,网格quality是判定网格质量的重要方面,使大其数值接近1,采用混合网格,泥浆槽部分采用结构网格划分,刀片部分采用非结构网格划分,刀片的边缘和刀面细化处理,如图2所示。

图2 刀片区域网格Fig.2 Domain of the blade grid

1.3 计算模型

采用商用软件Fluent16.1,泥浆设置为宾汉姆模型,近壁面处理采用标准壁面函数；采用混合模型(mixture model)对气液相互作用进行了表征；边界均设置为Wall；采用滑移网格(sliding mesh)描述刀片旋转；使用三维双精度求解器；压力-速度耦合方法采用SIMPLE算法及一阶迎风格式；湍流模型采用RNGk-ε模型；时间步长取为0.000 1 s,计算时间为1 s,在每个时间步长内设置最代次数为20次,收敛残差设为0.001。

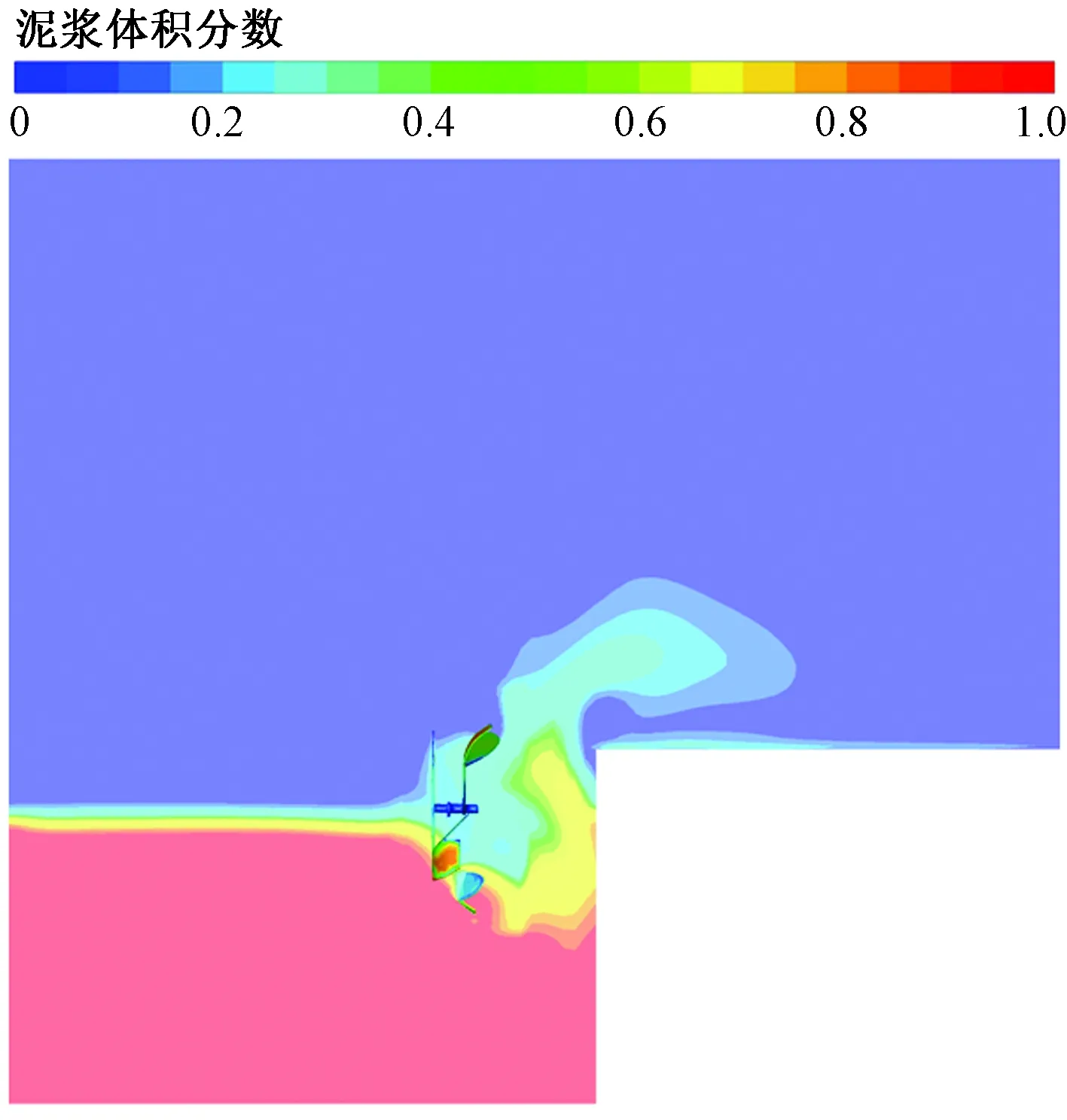
图3 泥浆体积分布Fig.3 Domain of the blade grid

2 数值模拟的网格无关性分析

现主要探讨模拟计算结果中的泥浆飞溅量、泥浆飞溅速度的网格无关性检验。设计9套网格数量对重要部分(刀片区域)和非重要部分(泥浆槽流体区域)进行不同程度的加密处理来进行网格无关性验证,模拟1 s后,观察其模拟结果,图3为刀轴横截面处泥浆体积分布图,图4所示为刀轴横截面处泥浆飞溅速度图。 数值模拟数据如表1所示,泥浆飞溅体积量是飞过距离刀轴一侧0.2 m横截面的泥浆体积量,如图5所示；平均侧面飞溅速度是距离刀轴一侧0.2 m处泥浆的平均飞溅速度,如图6所示。由图5、图6可知，网格数量对仿真模拟结果具有较大影响,当网格数量接近300×104时,模拟结果变化差异不大。

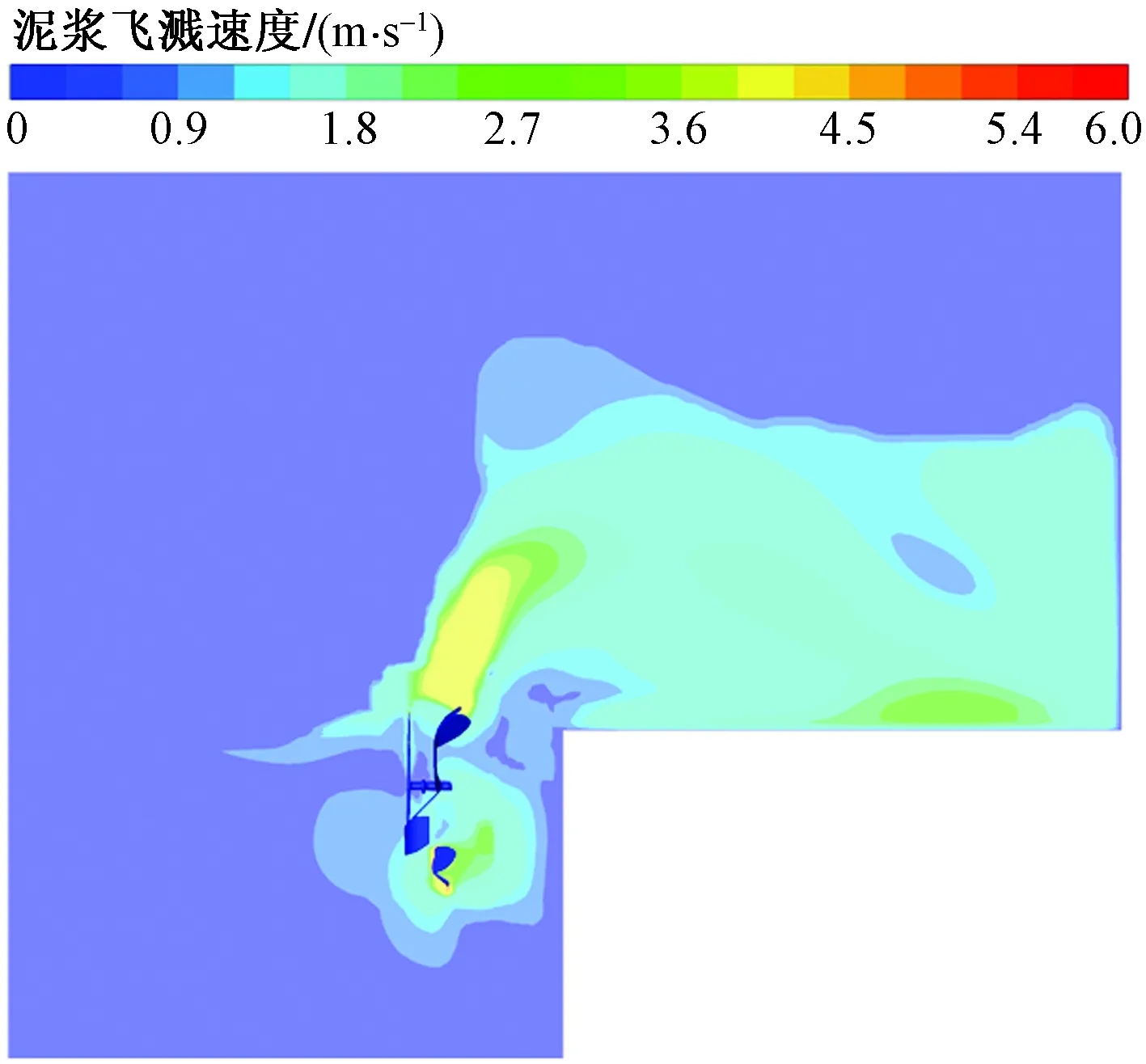
图4 泥浆飞溅速度Fig.4 Mud splash velocity

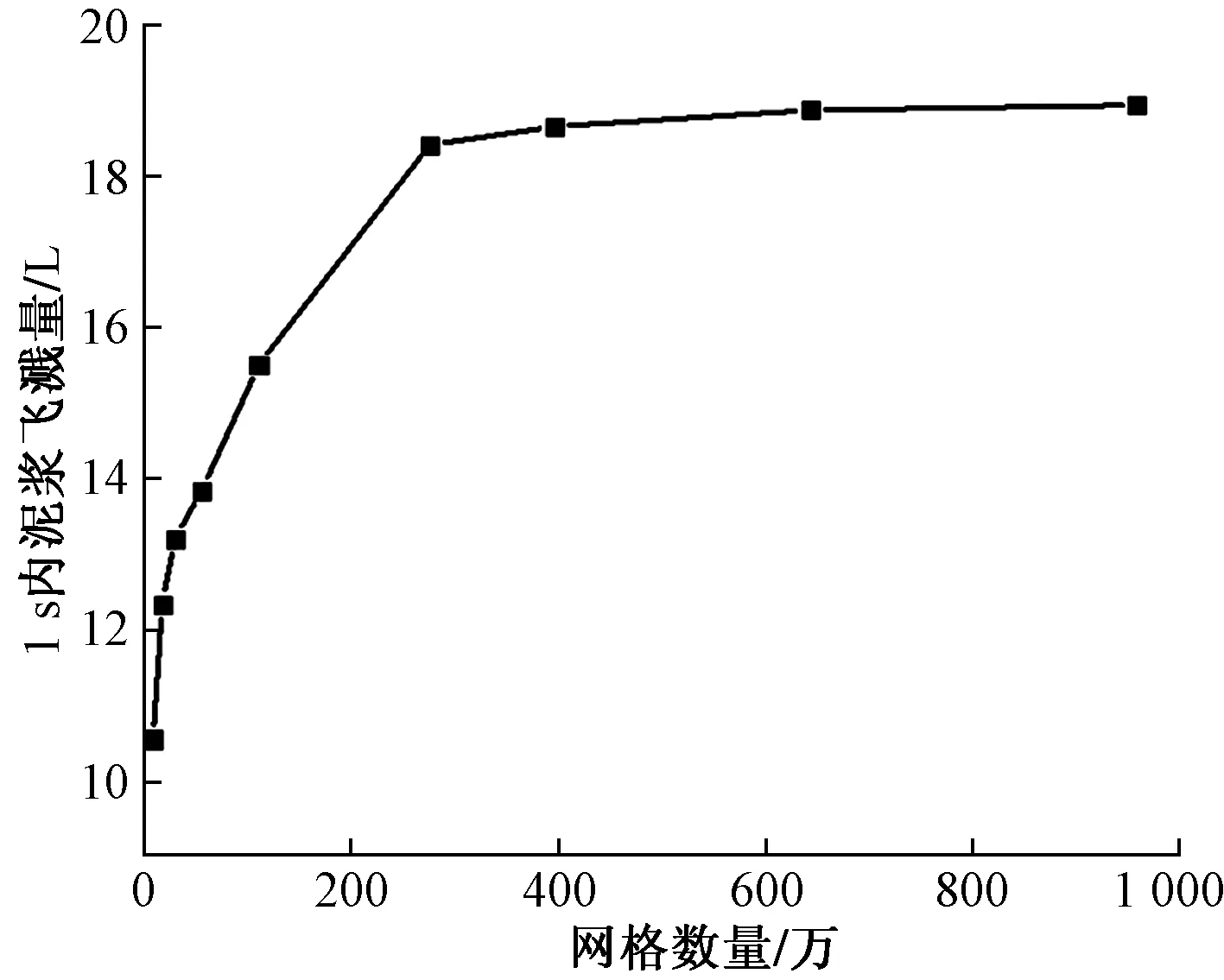
图5 泥浆飞溅体积量Fig.5 Mud splash volume

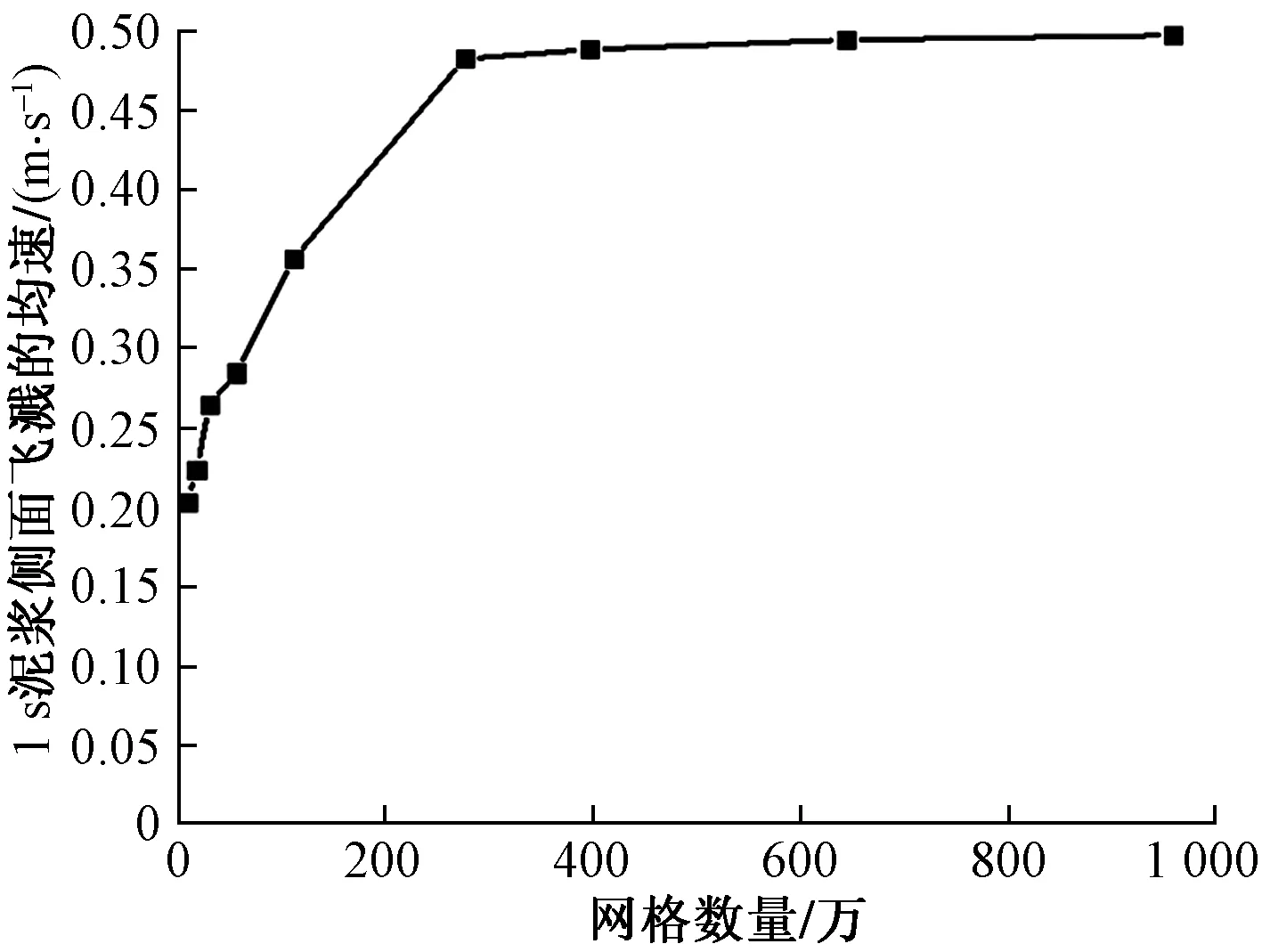
图6 泥浆平均测面飞溅速度Fig.6 Mud average side surface splash velocity

3 卡方检验

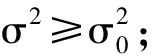
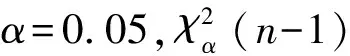
(1)

(2)

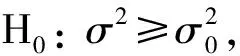
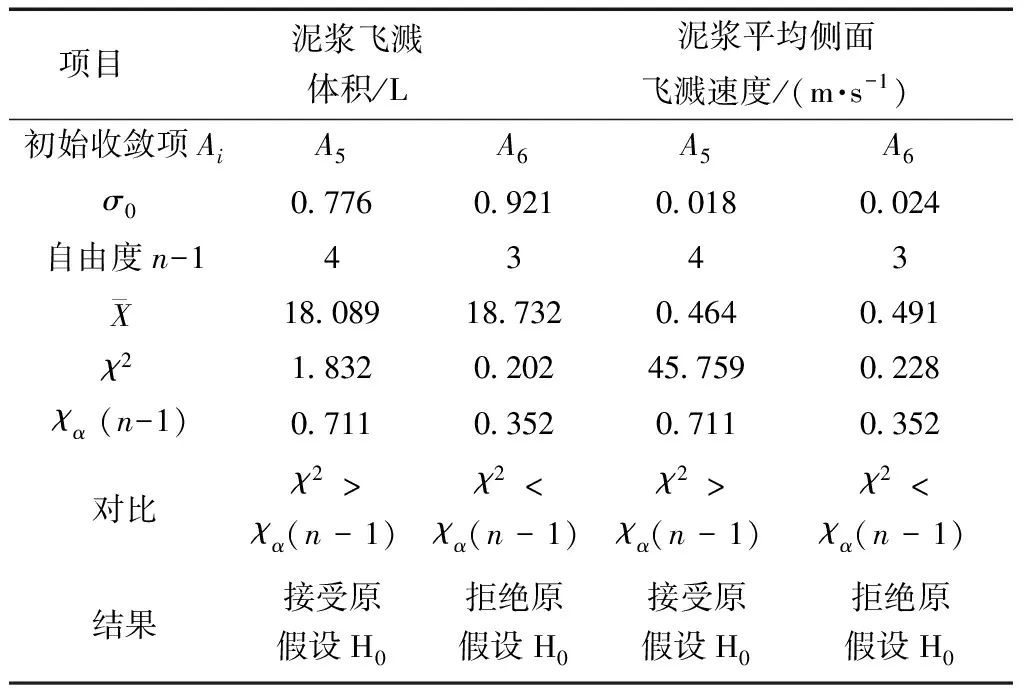
表1 泥浆飞溅收敛项卡方检验分析Table 1 Chi-square test analysis of mud splash convergence

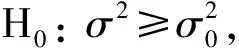
4 网格收敛性指数分析

下面引入网格收敛指数(grid convergence index,GCI)对网格独立性作进一步的讨论分析。

网格收敛误差ε为

(3)

式(3)中,f1、f2分别为细网格收敛解与粗网格收敛解。网格加密比定义为

(4)

式(4)中,hk为每个网格的平均间距,由式(4)计算得到:

(5)

式(5)中，ΔVi为每个网格单元的体积；Nk为每套网格的节点数。网格加密比还可以简化为

(6)

网格收敛指数GCI定义为

(7)

式(7)中，Fs为安全因子,当使用3套或3套以上网格来估算GCI时,Fs=1.25,P为收敛精度,取P=1.97。

GCI的计算结果如表2、表3所示。从A6开始,泥浆平均测面飞溅速度计算的GCI分别为2.60%、2.68%和1.57%,GCI均小于3%,泥浆飞溅量计算的GCI分别为2.77%、2.19%和1.88%,GCI均小于3%, 满足其网格收敛准则。

综上所述,卡方检验判定网格独立性与GCI判定网格收敛性的结果是一致的,此方案在网格接近300×104时数值模拟的计算值网格收敛。

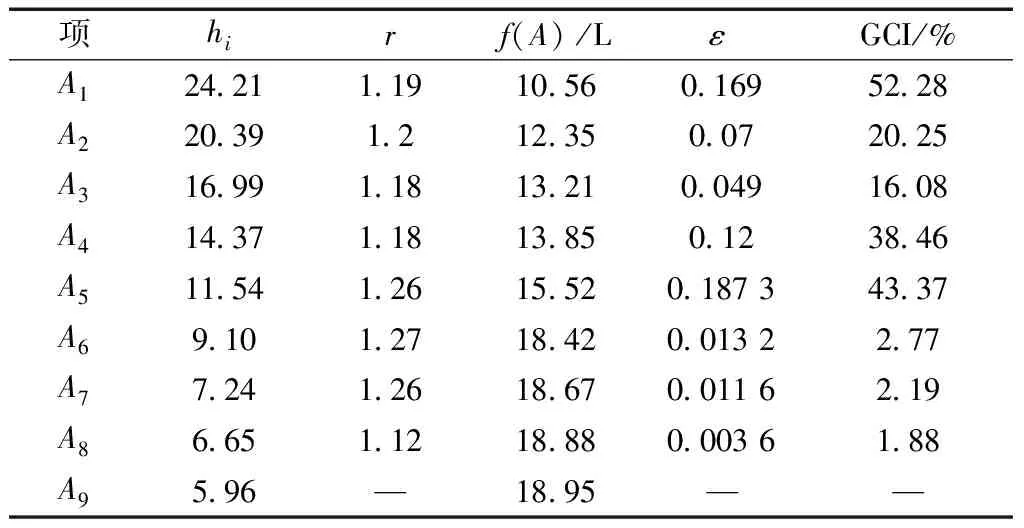
表2 泥浆飞溅量GCI收敛分析Table 2 GCI convergence of mud splash

注：hi为每个网格的平均间距,r为网格加密比，f(A)为泥浆飞溅量，ε为网格收敛误差，GCI为网格收敛指数。

表3 泥浆平均测面飞溅速度GCI收敛分析Table 3 GCI convergence of mud average side surface splashing velocity

注：f(V)为混浆飞溅速度。

5 试验验证

对卡方检验的准确性进行进一步的辅助验证,试验采用长方体泥浆槽,试验所用泥浆为福建省福州市闽侯县南通镇水稻田泥浆,泥浆高度为刀轴中心,时间为10月,温度为32 ℃,微耕机功率为4 kW,作业转速为40 rad/s,进行3次试验,1 s内泥浆槽泥浆下降的高度乘以槽的长和宽即为泥浆飞溅量,试验过程如图7所示,试验结果表明:1 s内泥浆飞溅量为16.97 L,与A9误差为8.72%。槽箱泥浆深度不够、机器无法立即达到所需转速等原因会引起泥浆飞溅量的减少,所以试验验证的数值和卡方检验的结果是趋近的。

图7 泥浆槽泥浆飞溅试验Fig.7 Experiment of mud splash in mud tank

6 结论

(1)基于较高质量的网格模型和合理的数值模拟方法,建立九种网格方案,对结果影响较大区域进行一定比例加密,泥浆飞溅平均速度和飞溅体积整体上均呈现出显著的上升趋势,且上升幅度越来越小,最后都在接近300×104网格左右能得到其网格无关性的结果。

(2)取标准差为一组中网格最少的参数的5%误差来进行卡方检验,泥浆飞溅量和平均侧面飞溅速度均从A6开始网格收敛。从A6开始的连续网格,网格收敛指数(GCI)均小于3%,当网格数目接近300万时,数值模拟的计算值与网格数目无关。实验验证1 s泥浆飞溅量与数值模拟误差为8.72%。

(3)通过网格收敛指数GCI来检验卡方检验用于网格无关性验证的方法,得出的结果是一致的,同时和实验验证的结果是趋近的,可得在一定的误差范围内借助卡方检验的方法验证网无关性是合理的。

(4)GCI方法更注重前后两项的联系,而卡方检验注重于某一范围内数据前后的变化和联系,能够在不同加密倍数情况下来判断网格收敛情况,本方法更加适用于找出趋于稳定后的最佳网格数量。相对而言,卡方检验也更加复杂细致。对于采用的均值未知的卡方检验方法用于网格无关性检验的关键是标准差的取值,基于不同的模型,标准差取值大小需要进一步研究。