基于离散裂缝网络模型的陆相页岩超临界CO2压裂滤失特征
2020-02-24乔红军
罗 攀, 乔红军, 李 哲, 黄 昊, 孙 晓, 贺 沛
(1.陕西延长石油(集团)有限责任公司研究院, 陕西省页岩气勘探开发工程技术研究中心,西安 710000;2.长庆油田采油六厂,定边 718600; 3.长庆油田采油十一厂,庆阳 745000)
鄂尔多斯盆地延长油田探区陆相页岩气资源潜力巨大,压裂是保证有效开发的重要技术方法[1-2]。CO2压裂可以降低储层水敏伤害,置换甲烷,封存CO2,节约水资源,这在压裂用水需求巨大的干旱地区有重要意义[3]。CO2在地下处于液态或超临界状态[4],黏度很低,扩散性极强,超临界CO2具有零表面张力[5],能进入许多常规压裂液难以进入的细微裂缝[6],而不形成滤饼,因此,其滤失特征应不同于常规压裂液。陆相页岩一般存在天然裂缝,这使液态/超临界CO2滤失与常规滤失差异更大。离散裂缝模型可以显式表示裂缝,因而可以更准确描述裂缝系统[7],张世明等基于离散裂缝模型求解了介质的等效渗透率[8],Yaghoubi基于离散裂缝模型建立了Barnett 页岩压裂模型[9],Xiong等基于三维离散裂缝网络模型研究了裂缝连通程度和导流能力对非线性流的影响[10]。陆相页岩存在砂纹夹层以及韵律性[11],有很强的非均质性[12],因此显式指定裂缝分布的离散裂缝网络模型[13]更适合于CO2滤失特征的研究。使用离散裂缝网络模型研究超临界CO2在压裂时的滤失特征,相对于双重介质模型的计算方法,本文的方法更适用于裂缝密度不均匀、裂缝角度特征明显以及不同裂缝尺寸的情形。使用山西组页岩实际地层参数进行计算,以期更好地研究CO2在山西组的滤失特征,准确预测CO2滤失量,优化CO2压裂程序。
1 超临界CO2物性与山西组裂缝特征
CO2在压力高于7.38 MPa、温度高于31.06 ℃时就处于超临界状态,而山西组地层压力在12 MPa以上,地层温度在65 ℃以上,如果CO2经过充分的换热到达地层,如通过光套管或环空注入时,则必定处于超临界状态。
王海柱等的研究表明,环空中CO2相态变化深度在990 m,钻杆内CO2相态变化深度为1 040 m[14]。山西组垂深在2 000 m以上,且水平井多使用光套管压裂,因此可以认为CO2在到达地层时已经经过了比较充分的换热,进入了超临界状态。图1所示为压力为12 MPa时CO2密度、黏度随温度的变化关系。

图1 CO2密度、黏度与温度的关系Fig.1 Relationship of temperature with CO2density and viscosity
上古生界山西组页岩平均孔隙度为0.77%,平均渗透率为0.04 mD,发育不同尺度的宏观裂缝和微裂缝(图2)。山西组暗色泥页岩岩心中可见构造缝、层理缝、成岩收缩缝和缝合线在内的多种裂缝类型,其中以构造缝和层理缝最为普遍。统计结果表明,岩心裂缝中大于13 cm的长裂缝最多,占42%[图2(a)],最长达4.5 m,大多为垂直缝,缝面平整,以发育在岩性均一、分选好的砂岩中为主;其次是长度小于6.5 cm的占31%,主要是发育在黑色泥页岩中的层理缝;长6.5~13 cm的裂缝占27%,角度在30°~60°之间,以45°居多,主要为发育在黑色泥岩中的滑脱缝。对于黑色泥岩中的裂缝而言,30°~50°斜交缝比例最高,占46%[图2(b)],其次是30°以下的低角度缝和水平缝,共占49%,高角度缝和垂直缝仅占5%。微裂缝长度平均9.65 mm,宽度平均20.32 μm,面缝率(未充填裂缝的总面积与薄片面积之比)为0.1%~0.3%,且75%的裂缝都处于开启状态。不同井的裂缝发育程度也存在一定差异,如Y108井岩心裂缝线密度为0.25条/cm,Y110井岩心裂缝线密度为0.67条/cm,Y154井岩心裂缝线密度为0.31条/cm[15-16]。山西组页岩存在不同尺度的天然裂缝[17],而液态/超临界CO2滤失性极强,即使是微小的裂缝也能进入[18],因此不能忽略裂缝的存在。

图2 山西组岩芯照片Fig.2 Core photographs of the Shanxi formation
2 离散裂缝网络滤失模型
超临界CO2在基质中的不稳定渗流模型可表示为
(1)
式(1)中:p为压力,Pa;t为时间,s;η为压力传导系数,m2/s。
超临界CO2在天然裂缝中的不稳定渗流模型可表示为
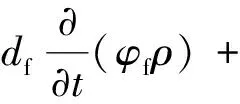
(2)
式(2)中:df为裂缝开度,m;φf为裂缝孔隙度;ρ为密度,kg/m3;T为裂缝切平面方向的梯度算子;u为裂缝内流速,m/s。u可由式(3)计算:

(3)
式(3)中:kf为裂缝渗透率,m2;μ为液态/超临界CO2黏度,Pa·s;p为裂缝内压力,Pa。
超临界CO2在基质中的扩散方程可以表示为

(4)

吸附项可以用式(5)表示为
(5)
式(5)中:kp为Freundlich吸附量,m3/kg,可由式(6)计算:
kp=kfc1/n
(6)
式(6)中:kf为Freundlich常数;n为Freundlich指数。
扩散项可以表示为

(7)
式(7)中:De为在多孔介质中的扩散系数,m2/s,可由式(8)计算:
(8)
式(8)中:Df为在地层液体中的扩散系数。
对流项中的速度由式(1)计算得到。内边界条件为注入压力和浓度:
p|x=0=pf
(9)
c|x=0=cf
(10)
外边界条件和初始条件为油层压力:
p|x=rd=pi
(11)
p|t=0=pi
(12)
相对于双重介质模型,离散裂缝模型可以显式地指定天然裂缝的位置、尺寸、形态以及在不同区域的分布[19,20],更能准确描述渗流状况。如图3所示,假设天然裂缝均为矩形,确定单条天然裂缝的形态需要使用裂缝长度、裂缝开度、裂缝高度、中心点位置、方位角、倾角、沿轴的旋转角度共计7个参数。如果总的裂缝条数为N,则裂缝系统可以描述为
(13)
式(13)中:x,y,z为裂缝中心点坐标,m;Li为裂缝的长度,m;df为裂缝的开度,m;H为裂缝的高度,m;φ为裂缝方位角,(°);θ为裂缝倾角,(°);α为裂缝沿轴的旋转角度,(°)。

图3 描述单条裂缝所需要的参数Fig.3 Parameters required for describing a single fracture
长和高的常见分布有指数分布、对数正态分布、伽马分布等[21],选用指数分布。指数分布的概率密度为式(14),累积密度为式(15)[22],某概率下对应的裂缝尺寸为式
(14)
(15)
(16)
式中:λ为裂缝长度平均值的倒数,1/m;u为某长度对应的概率;L为裂缝长度,m。
裂缝方位角、倾角、旋转角为指定区间的均匀分布:
γ=(γ1-γ2)r+γ2
(17)
式(17)中:γ为方位角、倾角、旋转角,(°);γ1为方位角、倾角、旋转角上限,(°);γ2为方位角、倾角、旋转角下限,(°);r为[0,1)之间均匀分布的随机数。
生成裂缝网络时,首先随机生成一系列裂缝的位置、尺寸、角度等参数,按裂缝参数生成裂缝,然后生成包在外围边长为1 m的正方体,最后对正方体和所有裂缝的集合进行差集运算,形成离散裂缝网络。设定正方体区域左侧的压力和右侧压差为1 MPa,便可求得单位面积上,压降为1 MPa/m时的CO2滤失速度,以此值乘以裂缝面积和实际压降,便可得到总的滤失速度。本文使用有限单元法对离散裂缝网络系统求解,网格剖分时,首先在裂缝上生成二维三角形网格,如图4所示,然后在此基础上形成求解域的四面体网格。

图4 离散裂缝的有限元网格Fig.4 Finite element mesh for discrete fractures
3 裂缝参数对超临界CO2滤失的影响
研究用到的参数如表1所示,其余参数根据研究对象不同略有调整。

表1 离散裂缝网络模拟的参数Table 1 Fracture parameters of discrete fracture network
3.1 裂缝条数(密度)对CO2滤失的影响
使用山西组地层渗透率和裂缝角度等实际参数,分析了不同裂缝条数(密度)对超临界CO2滤失速度的影响,得到的基质流量和裂缝流量如表2所示。可见随着裂缝数量(密度)的增多,裂缝之间的联通性增大,整个离散裂缝网络系统的复杂性增大,裂缝流量也会增大。
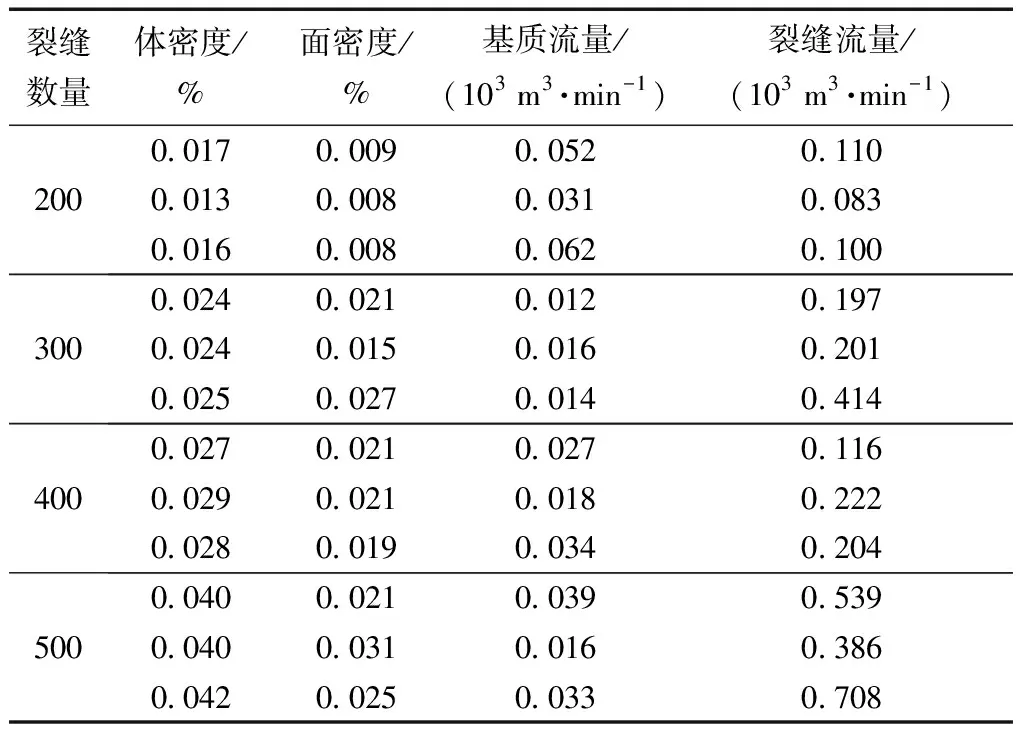
表2 不同裂缝数量(密度)的滤失速度Table 2 Leak-off rate with different number(density) of fractures
得到的裂缝条数(密度)与滤失速度的关系如图5所示,可见裂缝密度与裂缝流量呈正相关,且裂缝流量增加量也有随裂缝密度增大而增大的趋势,基质流量变化很小。裂缝流量比基质流量高一个数量级,因此,总流量与裂缝(数量)密度也正相关。

图5 裂缝密度对滤失速度的影响Fig.5 Effect of fracture density on leak off rate
3.2 裂缝尺寸对CO2滤失的影响
裂缝尺寸指裂缝长度、裂缝高度和裂缝开度。本文中裂缝尺寸在指定期望值后按指数分布随机生成。裂缝开度与裂缝渗透率的关系可表示为
(18)
式(18)中:φf为裂缝孔隙度;τf为裂缝曲折程度。
由于裂缝开度相对于长和高很小,难以在模型中显示出不同开度裂缝的区别,因此不给出建立的离散裂缝网络模型。使用山西组地层参数,研究了不同裂缝条数时裂缝开度对滤失速度的影响,结果如表3所示。
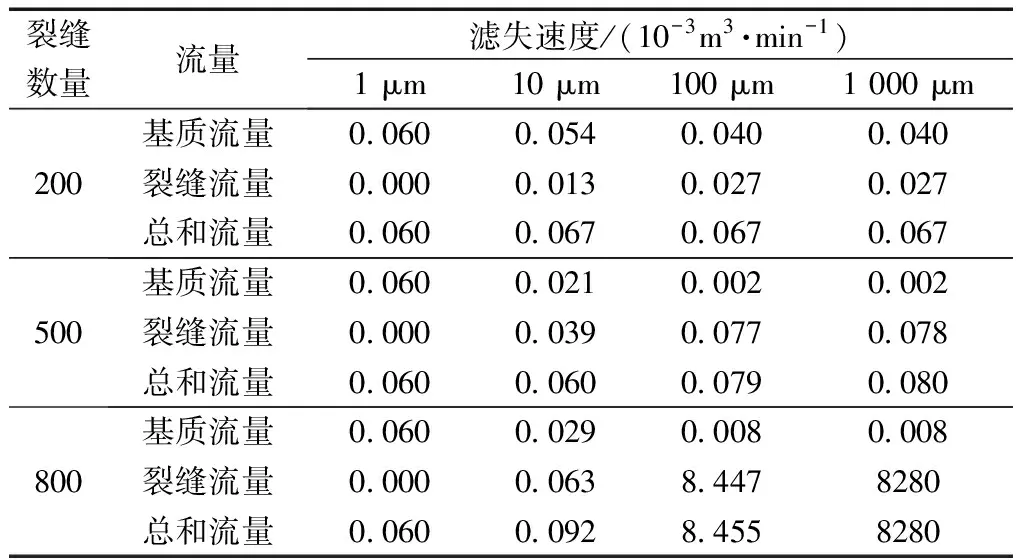
表3 不同裂缝开度的滤失速度Table 3 Leak-off rate with different width of fractures
当裂缝条数(密度)较低时,如200条或500条,此时裂缝间联通性很低,基质控制着滤失过程,裂缝开度对滤失速度的影响很小。当裂缝条数为800条时,裂缝联通性裂缝变好,开度增大导致滤失速度显著增加。裂缝渗透率与裂缝开度呈平方关系,在此基础上裂缝开度还会进一步影响裂缝过流断面的大小,因此裂缝流量与裂缝开度呈三次方关系。
就裂缝的几何形态而言,裂缝高度和裂缝长度是同一个概念,仅仅是观测的角度存在差异,因此讨论裂缝面积(A)与流量的关系。研究了200、300条天然裂缝情形下,裂缝面积期望值分别为0.01、0.02、0.03、0.04、0.05、0.06 m2时的滤失速度。得到的裂缝面积期望值与滤失速度的关系如图6所示。可见,面积期望值与滤失速度正相关,当裂缝条数(密度)更大时,裂缝面积期望值增大导致滤失速度增加更明显,这是因为裂缝较多时形成裂缝网络的可能性更大。

图6 裂缝面积期望值对滤失速度的影响Fig.6 Effect of expected value of fractures area on leak-off rate
3.3 裂缝角度对CO2滤失的影响
双重介质模型没有显式指定裂缝形态,因此难以考虑裂缝角度的影响,分析了不同方位角、度分布范围对滤失速度的影响。建立了不同裂缝方位角的DFN模型,这里假设了水力裂缝的方位角为0°,裂缝条数为300条,其余参数取值为山西页岩的实际参数。
得到的天然裂缝方位角与裂缝滤失速度之间的关系如图7所示,可见裂缝夹角与裂缝滤失速度之间呈正相关。
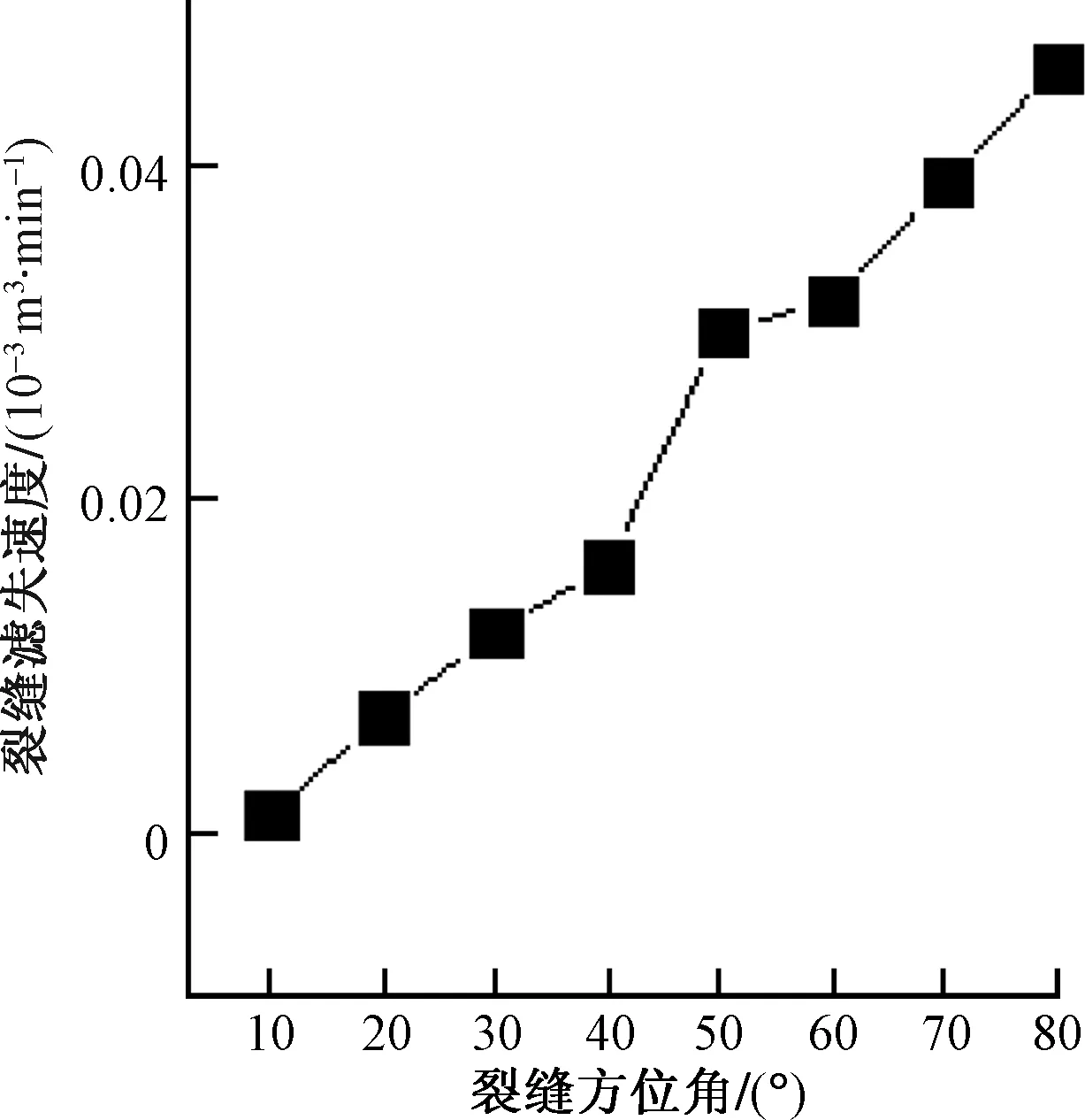
图7 不同方位角裂缝对滤失速度的影响Fig.7 Leak-off rate with different azimuth of fractures
分析了裂缝角度分布范围对压力分布以及滤失速度的影响,如图8所示,可见角度分布范围较大时裂缝复杂程度更大,滤失速度也更大。

图8 裂缝角度范围对滤失速度的影响Fig.8 Effect of fracture angle range on leak off rate
4 实例分析
鄂尔多斯盆地陆相页岩气YYP1-1井共进行了13段CO2前置压裂施工,地层压力约20 MPa,CO2泵注压力约55 MPa,微地震监测显示缝网基本在泵注CO2阶段就已经形成,得到的缝网几何大小如表4所示。根据前文所述地质条件建立了裂缝面密度约0.1%的DFN几何模型。得到压差为1 MPa/m时单位面积的滤失速度约为7.4×10-5m3/min。得到预测滤失速度与注入排量如图9所示,可见二者符合较好。在裂缝样本明晰的情形下,本文所建立模型可以较准确预测CO2滤失速度,从而预测裂缝滤失面积,预测裂缝长度,优化CO2压裂设计,具有一定实用价值。

表4 YYP1-1井裂缝监测数据Table 4 Fracture monitoring data of Well YYP1-1
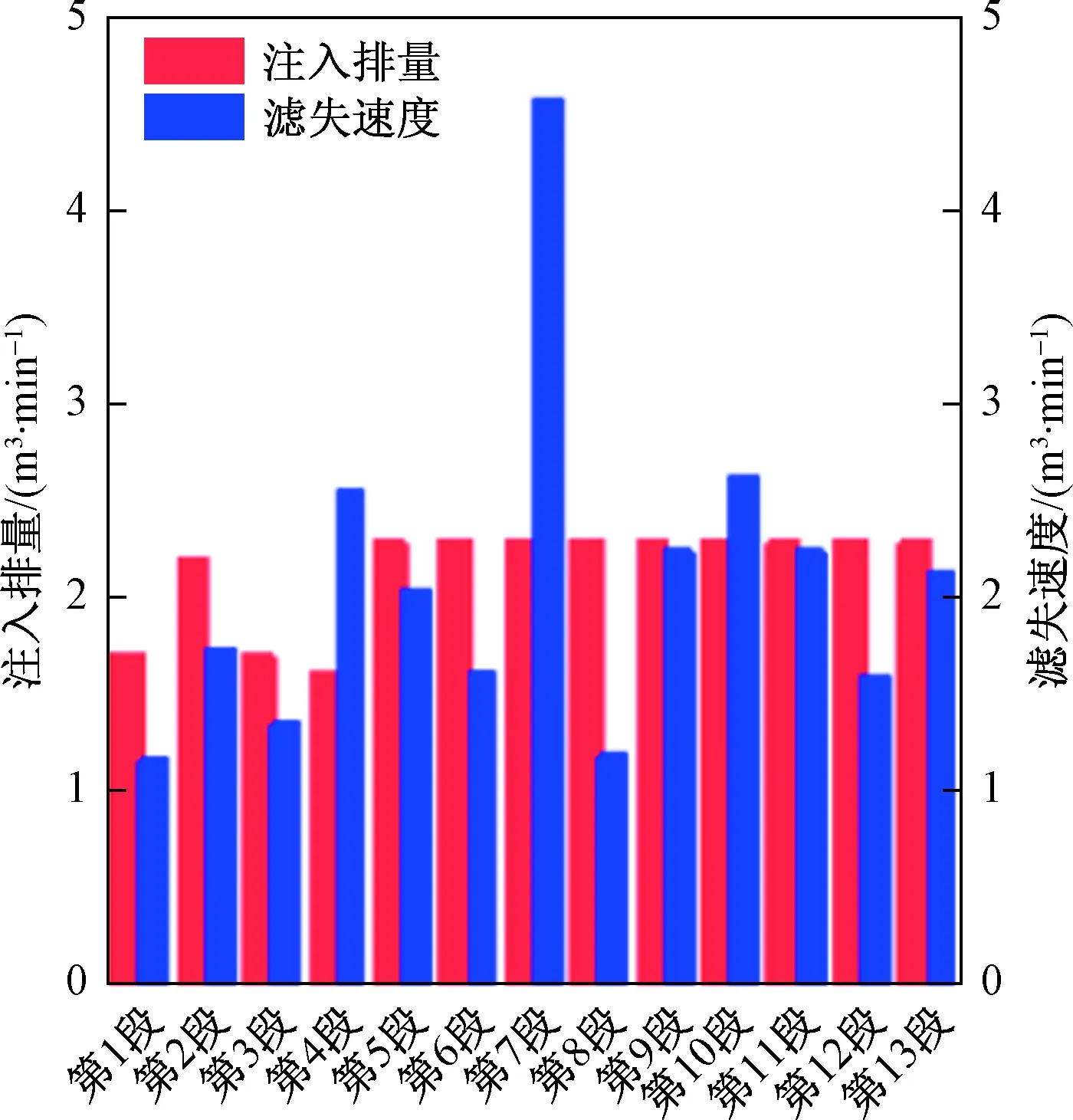
图9 预测滤失速度与注入排量Fig.9 Predicted leak-off rate and injection rate
5 结论
(1)超临界CO2滤失性很强,可以进入许多常规压裂液难以进入的空间。离散裂缝网络模型可以显式的创建裂缝网络,不受裂缝尺寸、角度不一致等限制,可以更准确的模拟超临界CO2的滤失。
(2)裂缝滤失速度与裂缝密度、裂缝尺寸正相关,天然裂缝与水力裂缝垂直时滤失速度最大,角度分布范围更大时滤失速度也更大。当裂缝联通性较好时裂缝成为主要渗流通道,基质速度略有下降,但变化不大。
(3)YYP1-1井现场施工数据对散裂缝网络模型验证结果表明,计算得到的CO2滤失速度与注入速度相差较小,因此本文模型具有较好准确性,可以为CO2压裂设计提供参考。
