沉管管段在浅水航道浮运中的下沉量预报
2019-12-25陈昌哲李泽为2李辉2盘俊吴静萍
陈昌哲,李泽为2,李辉2,盘俊,吴静萍
(1.武汉理工大学,a.交通学院;b.绿色船舶与海工装备技术研究中心,武汉 430063;2.交通部广州打捞局,广州 510000)
沉管法隧道凭借其埋深浅、地质适应能力强、两岸接线短,以及对岸线环境影响小等优势[1],已成为修建跨江越海通道的重要工法,并在国内外水下隧道工程中得到广泛应用,如港珠澳大桥[2]、韩国釜山巨济隧道[3]和荷兰MASS隧道[4]等。深中通道作为继港珠澳大桥之后又一世界级超大“隧、岛、桥”集群工程,将首次采用8车道特长海底沉管隧道,沉管隧道标准管段的尺寸达到165 m×46 m×10.6 m,而浮运作业水深仅为12.4 m。超长超大管段在如此浅的水域中进行浮运,浅水效应将导致管段受到“吸底”的水动力,引起管段发生下沉运动,颠簸的下沉运动将影响管段浮运稳定性和安全性,甚至可能导致管段发生触底事故。目前国内外对管段浮运的研究主要集中在浮运阻力[5]与拖航方案设计[6]等方面,对于管段浮运过程中下沉量[7]的研究,相关报道较少。本文研究了不同干舷与浮运速度下深中通道沉管管段的下沉运动。首先选择与管段浮运类似的正方体绕流进行数值模拟,将模拟结果与文献中的结果进行对比,验证数值模拟的计算精度。然后采用定常计算,数值模拟得到管段在不同下沉位置与水流速度下的水动力。最后将水动力中的“吸底”力进行拉格朗日插值拟合,并基于牛顿第二定律进行求解得到下沉运动的时历曲线,从而得到最大下沉量。比较最大下沉量与干舷的大小,判断管段在浮运过程中是否能够保持浮出水面,借此分析出不同干舷下管段的最大浮运速度,供工程应用参考。
1 管段水动力数值模拟精度验证
1.1 计算模型
沉管管段为长方体,水流在边角处即发生流动分离,产生大量漩涡,复杂的漩涡流动增加了数值模拟的难度。选取外形类似且有文献给出阻力系数结果的正方体(图1)进行绕流数值模拟。

图1 正方体无限流场绕流示意
1.2 计算工况
选取正方体边长l分别为1 m和10 m,雷诺数为10 000、25 000、50 000、75 000、100 000,按照雷诺数相似准则确定流速,计算工况见表1。
1.3 计算精度分析
Re在104~105之间时,正方体在无限流域中的阻力系数[CD]文献=1.05[8],将数值模拟得到的阻力系数CD与文献中的阻力系数[CD]文献进行比较,相对误差η见图2。
(1)

表1 计算工况
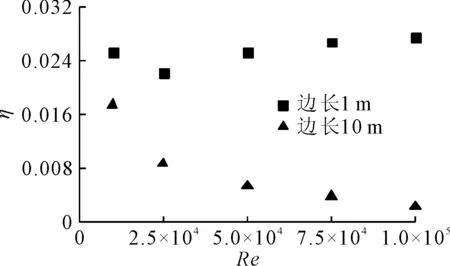
图2 两种边长下的阻力系数相对误差η
由图2可见,正方体边长为10 m时的阻力系数相对误差普遍小于边长为1 m时,说明所采用的数值模拟方法计算大尺度方体模型水动力的精度要高于小尺度方体模型。因此,计算沉管管段模型均采用原型尺度。同时,图2中阻力系数相对误差均小于3%,足以满足工程精度要求。
2 管段水动力和最大下沉量计算
2.1 管段主尺度
深中通道沉管隧道段的标准管段为长方体结构,主尺度L×B×H=165 m×46 m×10.6 m,总质量M=77 000 t,浮运作业水深H水=12.4 m,干舷可变。
2.2 计算工况
2.2.1 管段下沉量计算工况
实际管段浮运时,一般吃水较大,干舷值的范围为0.10~0.25 m[9]。取管段下沉之前的初始干舷H干舷=0.1、0.2、0.3、0.4 m。
管段在浅水航道中的浮运速度,工程经验一般为1.0~2.0 m/s[10]。基于提升浮运速度的工程需求,取浮运速度U=1.0、1.5、2.0、2.5 m/s,略超经验范围。
如此,选取4种初始干舷,4种浮运速度,共计16种管段下沉量计算工况。
2.2.2 管段水动力计算工况
当管段发生下沉运动时,在水中的位置发生变化,因此,需要计算下沉运动可能到达的不同位置的水动力,利用水动力计算得到管段的下沉量。
管段的初始干舷虽然不同,但是在下沉运动过程中,某一瞬时的位置可能完全相同,那么在相同浮运速度下水动力大小也完全相同。比如,初始干舷H干舷=0.1 m且管段未下沉,与初始干舷H干舷=0.2 m且管段下沉了0.1 m,两者的管段底面与水底之间的间隙间距H间隙均为1.9 m,水动力大小相同,为同一个计算工况。所以水动力计算中,除了浮运速度以外,还以H间隙为参数设置工况。
H间隙的最大值出现在初始干舷H干舷=0.4 m且管段未下沉时,此时H间隙=2.2 m。最小值出现在管段刚好完全浸没时,此时H间隙=1.8 m。管段完全浸没之后,由于惯性,下沉运动可能还将继续(这只是计算状态,实际工程中管段应保持在水面之上的作业状态),导致H间隙小于1.8 m。根据下沉运动预计算,统一取H间隙=1.7~2.2 m。本文计算取H间隙=0.5~2.2 m,间隔0.1 m,共设置18个水底间隙H间隙。
这样,确定4个浮运速度,18个水底间隙H间隙,共计72种管段水动力计算工况,其他位置的管段水动力采用拉格朗日插值获得。
2.3 管段水动力计算
2.3.1 管段水动力计算模型
下沉运动过程中,管段可能完全没入水中,计算模型分为顶面露出水面和顶面入水两种情况,由于沉管浮运速度较慢,忽略自由液面的兴波影响,几何模型取管段水下部分,见图3。
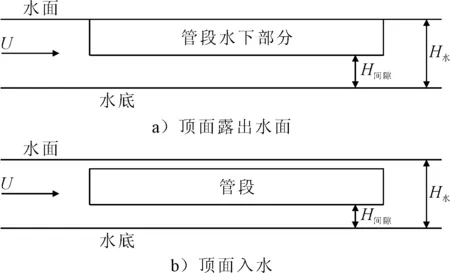
图3 管段水动力几何模型
2.3.2 速度和压强分布
速度分布用于显示管段底部与水底之间的高速间隙流动,压强分布用于表明管段表面压强分布不均匀引起的压差阻力和下沉力。
以H间隙=2.2 m,U=1 m/s的计算工况为例。
管段中纵剖面的局部流场速度分布见图4。
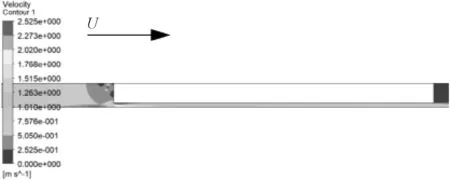
图4 中纵剖面局部速度分布
可以看出,在管段底面与水底壁面之间形成了狭窄的间隙,而且由于水的黏性,在管段底面与水底壁面处分别形成了低速边界层,间隙内部水流速度比外部水流速度大,采用伯努利方程可推断表明,该处的压强较其他位置小。
管段表面压强分布图见图5,可以看出,管段迎流面主要受到正压力,尾部为负压区,造成了管段所受的压差阻力;而管段底面为负压区,上下表面的压差产生了下沉力,从而导致管段下沉。

图5 管段表面压强分布
2.3.3 管段水动力
管段水动力计算结果见图6。
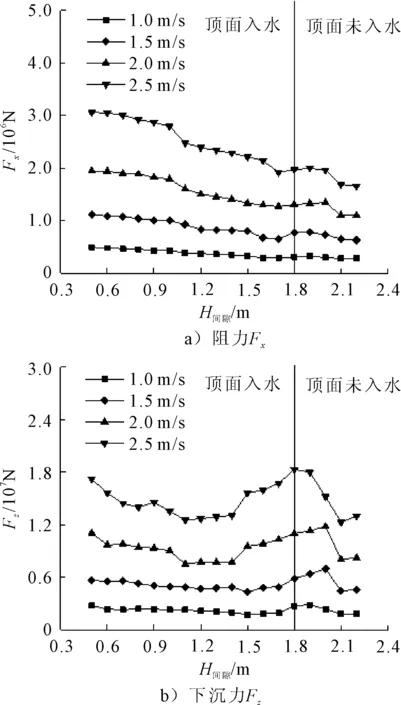
图6 管段水动力计算结果
图6表明了阻力和下沉力在不同来流速度U下随H间隙的变化规律。其中,1.8 m≤H间隙<2.2 m为管段顶面露出水面的工况;0.5 m≤H间隙<1.8 m为管段顶面入水的工况。
1)在相同的H间隙下,高流速时的管段阻力和下沉力均大于低流速时。
2)图6a)中,在相同水流速度U下,总的来说,阻力随H间隙的增加呈下降趋势,但在H间隙=1.8~2.0 m范围内稍有波动。
3)图6b)中,在相同水流速度U下,下沉力在H间隙=1.0~1.5 m范围内出现谷值,H间隙=1.8~2.0 m范围内出现峰值。
2.4 管段最大下沉量计算
2.4.1 下沉运动的计算方法
管段浮运时,下沉运动受力分析见图7。

图7 管段竖直方向受力
图中F浮为浮力与重力的差值,称为净浮力,当管段在初始干舷位置时,浮力与重力平衡,F浮=0;当发生下沉运动后,浮力不再与重力平衡,从而出现净浮力。F阻是由于下沉运动引起的流体阻力,该力与净浮力F浮的方向一致,阻碍管段的下沉运动。Fz为下沉力。
竖直方向上各力的计算表达式如下。
F浮=ρgLBH下
(2)
式中:ρ为海水密度,ρ=1 025 kg/m3;g为重力加速度,g=9.8 m/s2;H下为瞬时下沉位移,管段处于初始干舷的平衡状态时,H下=0。

(3)
式中:V下为管段的瞬时下沉速度;Cd为竖向阻力系数,取Cd=1.05的常数。
关于下沉力Fz,已在2.3.3节中得到了离散的数据点,采用拉格朗日插值方法获得不同浮运速度U下每一瞬时位置H下的下沉力Fz。
将竖直方向的作用力代入牛顿第二定理,时间步进计算管段的下沉运动,即可获得管段在不同时刻的加速度a、下沉速度V下以及下沉位移H下。
2.4.2 最大下沉量
H干舷=0.4 m,U=1.0 m/s时下沉运动的时历曲线见图8。
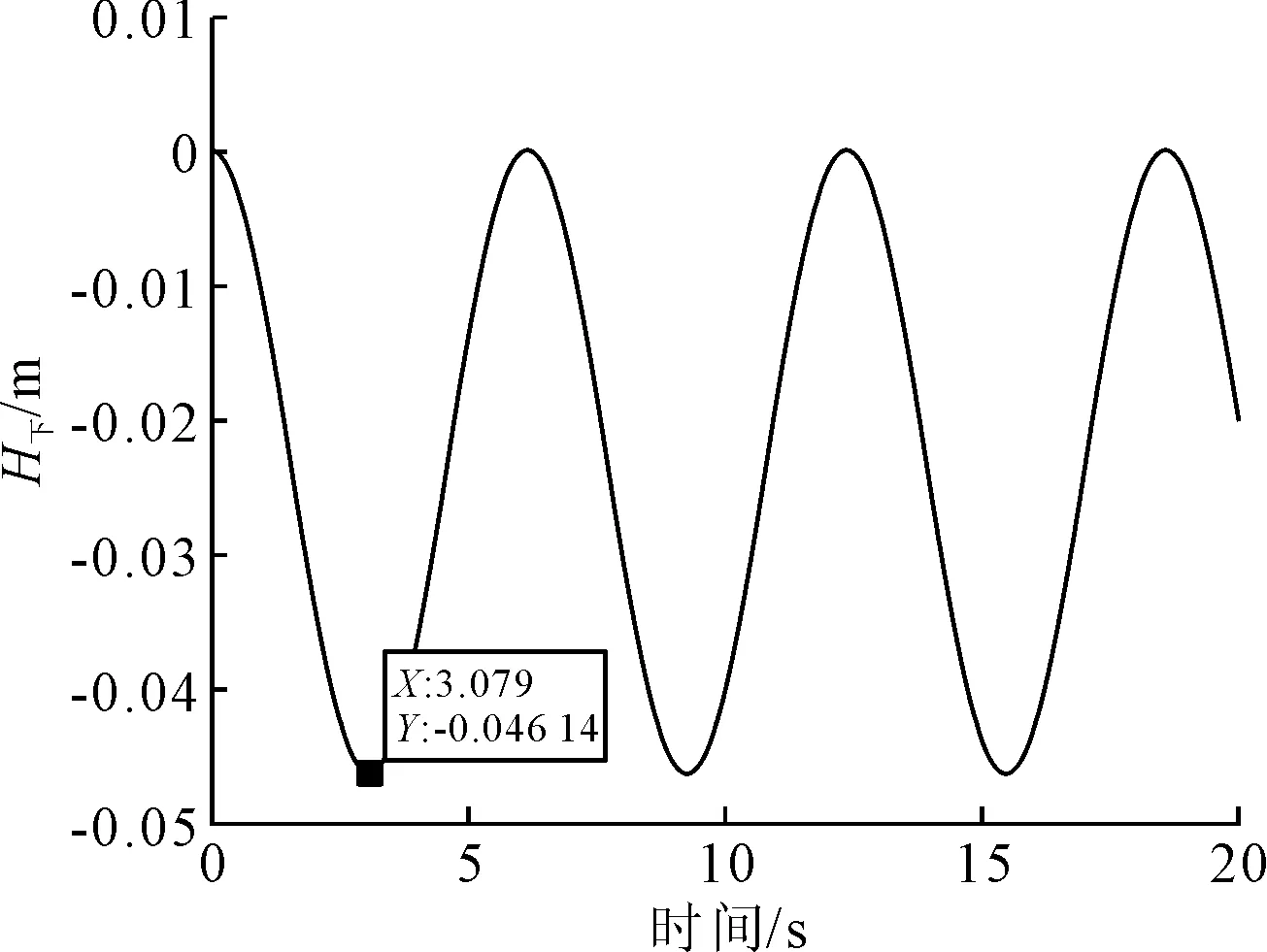
图8 下沉运动H下的时历曲线
由图8可见,H下的最小值出现在管段下沉的最低位置,该最小值的绝对值即为管段的最大下沉量H下max。
不同初始干舷H干舷与浮运速度U下的最大下沉量H下max计算结果见表2。表中字体加粗的最大下沉量H下max数据代表在该干舷与浮运速度下,最大下沉量小于初始干舷,浮运安全;未加粗的最大下沉量H下max数据代表在该干舷与浮运速度下,最大下沉量大于初始干舷,浮运危险;-代表下沉力大于沉管的最大净浮力,沉管将沉底。
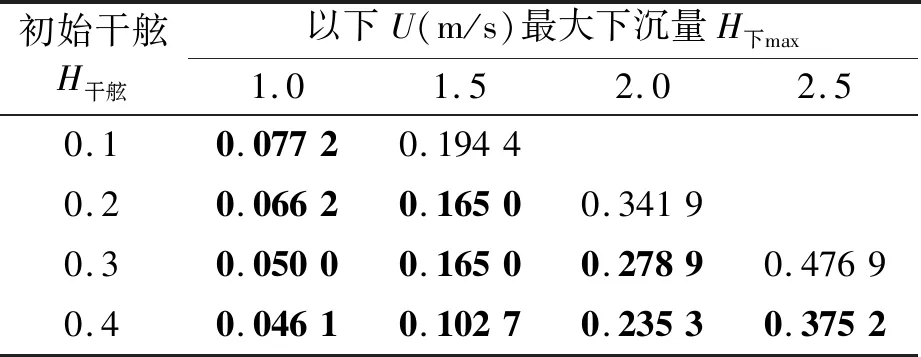
表2 最大下沉量H下max m
由表2可见,当初始干舷较小或浮运速度较大时,管段最大下沉量较大。为使管段顶面能够保持露出水面,管段初始干舷H干舷=0.1、0.2、0.3、0.4 m时对应的最大浮运速度分别为1.0、1.5、2.0、2.5 m/s。
3 结论
在本文计算参数范围内,随着浮运速度的增加,管段所受的阻力与下沉力均随之增加。阻力随H间隙的增加几乎单调递减,下沉力在H间隙=1.8~2.0 m范围内出现最大值。
对于本文计算的深中通道沉管管段,初始干舷为0.1,0.2,0.3,0.4 m时,保持管段顶面能够露出水面的最大浮运速度分别为1.0,1.5,2.0,2.5 m/s。但由于在计算过程中,并未考虑实际工程中的水流环境影响,工程中的水流速度会与沉管浮运速度(指对地速度)矢量叠加,增大或减小沉管与水体之间的相对速度,顺流时相对速度较小,浮运速度可选择相应增加,逆流时相对速度较大,浮运速度则必须比计算值要小。
后续研究应考虑加入风浪流等实际工程作业条件,得到更有针对性的沉管管段水动力大小与下沉量。
