无杆牵引系统不平路面工况下起落架载荷仿真
2019-08-01王立文孙艳坤
王立文,刘 冰,孙艳坤,张 威
(中国民航大学a.地面特种设备研究基地;b.航空工程学院,天津 300300)
飞机牵引技术主要应用于机场跑道、滑行道等处飞机及其大型部件的移动,是涉及牵引装置和机场条件等因素的综合技术。现代飞机对地面运行特性的要求日益提高,牵引系统运行过程中可能出现坑槽、降起、错台等损坏路面的情况。飞机无杆牵引过程中,这些不平整道面对飞机起落架产生的牵引载荷可能会超出使用限制,从而造成起落架损坏。为避免事故发生,需要研究牵引过程中特殊路面对飞机前起落架的影响,从而对牵引车-飞机系统的安全性进行正确的评估和预测。国内外关于飞机牵引载荷对飞机起落架影响的早期研究中,张海等[1]对牵引车牵引飞机实施启动、匀速运行、紧急刹车的过程进行仿真,考察牵引载荷引起的前起落架下阻力臂载荷变化,在有杆牵引车基础上建立牵引模型。有学者通过CATIA 和Adams建立牵引系统模型,研究了前起落架在飞机经过不同凹坑和凸起时的受力情况[2-4],但其研究结果是在有杆牵引车模型下得到的,随着无杆牵引车的广泛应用,对无杆牵引情况的研究也尤为重要。Schmidt[5]研究了冰雪路面和除冰后的路面工况对牵引系统的性能影响,主要集中在牵引车的选择和制动要求,但未说明此种工况下是否会对前起落架造成影响。Wang 等[6]对飞机起飞、着陆和牵引过程中起落架在正常牵引情况下受到的载荷进行了测量此处少一句分析。综上研究,利用SolidWorks 和Adams 建立无杆牵引车-飞机模型,分析牵引系统在不同宽度、深度(高度)的凹坑或凸起路面状态下飞机前起落架的受载情况,对两种凹坑(凸起)路况下的载荷峰值变化进行了模拟,对牵引车和主机轮经过凹坑时的载荷进行了对比分析,预测并解决实际牵引过程中可能出现的突发问题,从而为起落架的研究提供参考。
1 理论模型的建立
1.1 路面模型
不平路面的研究主要考虑凹坑和凸起两种状态,二者主要影响轮胎重心竖直方向的位移变化,从而导致牵引车和飞机在竖直方向发生振动。为简化模型,可将凸起路面作为一种特殊的凹坑来处理。凹坑与轮胎的位置关系主要有2 种,如图1所示。A 型凹坑中,轮胎可与凹坑底部相切,此时轮胎竖直方向的位移只与凹坑的深度h1有关;B 型凹坑中,轮胎与凹坑底部相离,轮胎竖直方向的位移与凹坑的宽度L 相关。

图1 凹坑与轮胎的位置关系模型Fig.1 Position relation model of pits and tires
为了后续数值选取和模型的动力学仿真,对轮胎竖直方向的位移与两类凹坑的关系进行了理论推导。对于图1(a)中的A 型凹坑模型,有

其中:h 为轮胎竖直方向的位移;h1为凹坑深度;R 为轮胎直径;L 为凹坑宽度,将式(1)~式(3)联立得

当凹坑深度h1、轮胎直径R 与凹坑宽度L 满足式(4)时,将会出现图1(a)中A 型凹坑的位置关系。如果凹坑宽度L 很大,可将A 型凹坑视为路面凸起,即将凸起作为凹坑的一种特殊状态,从而简化模型,便于理论推导。同理可得,当凹坑底部与轮胎相离时,凹坑深度与轮胎竖直方向的位移无关,如图1(b)中,B 型凹坑所示的位置关系,凹坑深度h1、轮胎直径R 与凹坑宽度L 满足以下等式

对于B 型凹坑模型,有

1.2 飞机起落架模型
以支柱式起落架为研究对象,其一般由支柱、缓冲器和机轮等组成,缓冲器一般为油气缓冲器,由外筒和活塞杆组成的封闭空间中存在液压油和压缩空气。压缩空气可视为空气弹簧,外筒内部的油液阻尼孔和活塞杆内部的油针可视为阻尼器,如图2所示。

图2 飞机整体理论模型Fig.2 Theoretical model of aircraft
图2中,O 为飞机重心位置;y 为飞机重心的位移;θ 为飞机绕重心的旋转角度;M1为前起落架空气弹簧所支撑的质量,包括分配在前起落架上的机身质量、前起落架外筒质量等;M2为主起落架空气弹簧所支撑的质量,包括分配到主起落架的等效机身质量、主起落架外筒质量等;m1为前起落架内筒、刹车和机轮的总质量;m2为牵引车的质量;m3为主起落架内筒、机轮、刹车等机构的总质量。k1,c1,k2,c2和k3,c3分别为前机轮轮胎、牵引车轮胎和主机轮轮胎的线性刚度和线性阻尼系数。缓冲支柱力Fi可用空气弹簧力Fai、油液阻尼力Fli和缓冲器外壳与活塞的摩擦力Ffi三者之和来表示[7-8],即
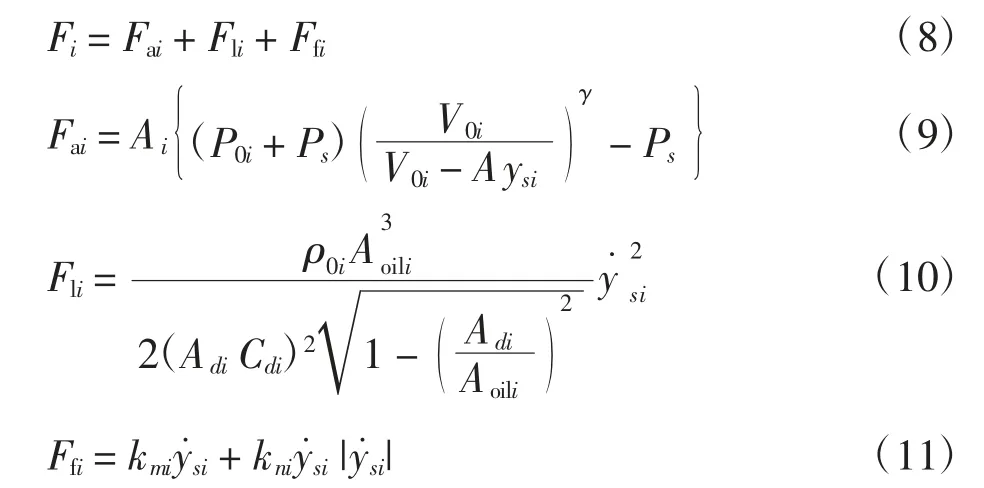
其中:Ai为起落架活塞的有效面积;P0i为起落架缓冲器初始气压;Ps为外界大气压;V0i为前起落架缓冲器的初始容积;γ 为多变指数,一般取1.1~1.3;ρ0i为前起落架缓冲器的油液密度;Aoili为前起落架缓冲器油液作用的有效面积;Cdi为缓冲器油液卸荷系数;kmi和kni为经验参数,用于模拟摩擦力;i=1,2,其中1 为前起落架,2 为主起落架;ys1=y1-y2为前起落架缓冲器的冲程;ys2=y4-y5为主起落架缓冲器的冲程。
牵引车拖动飞机经过不平路面时有两种情况,第1 种情况是当牵引车经过凹坑或者凸起,主起落架的机轮还处于平面路况下,路面状况对前起落架振动的影响,由于主起落架对前起落架的受力影响很小,只需单独对前起落架进行分析,如图2虚线部分所示。M1质量块受到缓冲支柱施加给M1的力F1和自身重力M1g,缓冲支柱施加给质量块M1的力与运动行程和速度成非线性关系。前起落架的轮胎力与y2和y3的位移和速度大小有关,则

由于飞机前起落架的轮胎更接近于无杆牵引车的后方,且牵引车的后轮胎处于不平路面位置区域,则牵引车后轮胎的轮胎力Ft21还应考虑地面的位移变化,牵引车前轮胎的轮胎力Ft22只需考虑y3的变化,即

其中,yg为路面变化函数,当路面为凹坑或凸起时,yg=h,于是可得前起落架的动力学方程为

第2 种情况是主起落架经过凹坑或凸起路面时,牵引车和前起落架在平面状态下对前起落架的影响,如图2中实线部分所示。由于主起落架在竖直方向发生了位移,使飞机机身发生了小角度偏转,则

此时牵引车处在平坦路面,牵引车的轮胎力Ft2=Ft21=Ft22,即

则主机轮的轮胎力为

对于前起落架和主起落架构成的整体模型,可得动力学方程为

2 仿真模型的建立
飞机无杆牵引车模型以Mototok Spacer 系列牵引车和B737-300 为参考原型,通过SolidWorks 为飞机机身、前起落架、主起落架和无杆牵引车建模,转换为Parasolid 格式导入仿真软件Adams,并创建各个机构之间的约束关系,建立彼此之间的连接[9],为了更好地表现凹坑或凸起路面、实现路面可视化,需建立3D 仿真路面。此时在该仿真模型中,飞机与牵引车轮胎均采用Fiala 轮胎模型[10],通过查阅飞机维护手册以及飞机设计手册相关参数,得到飞机与牵引车模型所需数据,如表1所示。

表1 飞机与牵引车模型输入参数Tab.1 Input parameters of aircraft and tractor models
在SolidWorks 和Adams 联合建立的飞机牵引车仿真模型中输入所需数据,按照实际模型建立相应的约束关系,经过调试和运行确认模型准确无误后,得到如图3所示的模型。
在凹坑或凸起路面进行动力学仿真,需选择合适的凹坑或凸起数据,为了辨别所选数据是否满足图1中的两种路面模型,只需判断数据是否满足式(4)和式(5)。

图3 Adams 动力学仿真模型Fig.3 Dynamic simulation model in Adams
2.1 情况一
当牵引车经过凹坑或凸起,主起落架的机轮还处于平面路况下,对于情况一的A 型凹坑,由于牵引车轮胎接触到了凹坑最底部,牵引车轮胎竖直方向的位移主要取决于凹坑的深度,凹坑宽度的变化不影响分析结果,故前起落架缓冲支柱所受载荷的最大副值不变。
当凹坑宽度不变时,凹坑深度不同,飞机牵引系统匀速运动,分析前起落架缓冲支柱载荷的变化。对于B 型凹坑,由于牵引车的轮胎没有接触到凹坑最底部,当凹坑宽度不变时,轮胎下降位移不随凹坑深度变化,此时只需考虑A 型凹坑的变化。如图4所示,A型凹坑宽度L=500 mm 时,由飞机牵引系统经过4 种不同深度的凹坑时缓冲支柱的载荷变化曲线可以看到,经过凹坑的任意一个边缘时,凹坑深度变大则前起落架缓冲支柱的载荷副值也将变大;当凹坑深度h1<30 mm 时,经过第1 个凹坑边缘时的载荷大于第2 个边缘;当凹坑深度h1>30 mm 时,经过第1 个凹坑边缘时的载荷小于第2 个边缘,且随着深度增加,载荷变化趋缓。由图5可知,缓冲支柱的峰值载荷随凹坑深度的增加而增大,两边缘处的载荷也逐渐变大。
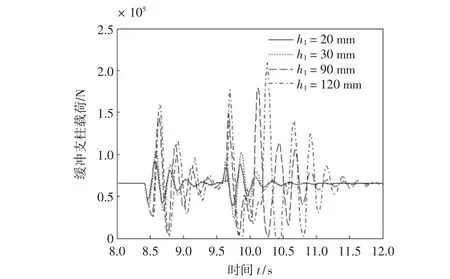
图4 A 型凹坑下前起落架缓冲支柱受力图Fig.4 Force on nose landing gear shock strut in Pit A

图5 不同凹坑深度下前起落架缓冲支柱载荷曲线Fig.5 Force on nose landing gear shock strut under different depths of pits
当凹坑深度h1=15 mm 时,牵引车以5 km/h 的速度匀速牵引飞机经过4 种不同宽度的凹坑,对飞机前起落架缓冲支柱的影响如图6所示。在8.4 s 时刻牵引车开始经过凹坑,根据凹坑宽度和深度,由式(5)可知此为B 型凹坑,牵引车轮胎没有接触到凹坑最底端。对比分析4 种凹坑,飞机前起落架在凹坑宽度L=50 mm时缓冲支柱受到的载荷副值最大,且随着宽度的增加载荷变化越慢。如图7所示,当凹坑宽度L<40 mm时,载荷值随凹坑宽度的增加而变大;当L=40 mm 时,B型凹坑下缓冲支柱载荷达到最大值;当40mm<L<100mm时,缓冲支柱载荷随凹坑宽度的增加逐渐变小,然后趋于平稳,最后随宽度增加先增大后减小。

图6 B 型凹坑下前起落架缓冲支柱受力图Fig.6 Force on nose landing gear shock strut in Pit B

图7 不同凹坑宽度下前起落架缓冲支柱载荷曲线Fig.7 Maximum force on nose landing gear shock strut under different widths of pits
2.2 情况二
前起落架在牵引车举抱下处于平面状态,主起落架处于凹坑状态,当飞机牵引系统以匀速行驶时,主起落架与轮胎的位移变化影响到飞机机身的位移变化,从而对前起落架缓冲支柱的载荷造成影响。由于主起落架轮胎接触到A 型凹坑的最底部,此时主起落架的位移变化与凹坑宽度无关,仅受凹坑深度影响。
当凹坑宽度不变(L=800 mm)、深度不同、飞机牵引系统匀速运动时,分析前起落架缓冲支柱载荷的变化。同理,只需考虑A 型凹坑下的变化情况。如图8~9 所示,当主起落架轮胎经过凹坑时,凹坑边缘使轮胎发生位移突变,随着凹坑深度增大,在经过任意一个凹坑边缘时,前起落架缓冲支柱受到的载荷也在增大,且在第2 边缘受到的载荷大于第1 边缘,此工况下的峰值载荷为第2 边缘时的载荷。且随凹坑深度的增加,第2 边缘与第1 边缘的峰值载荷差越来越大。
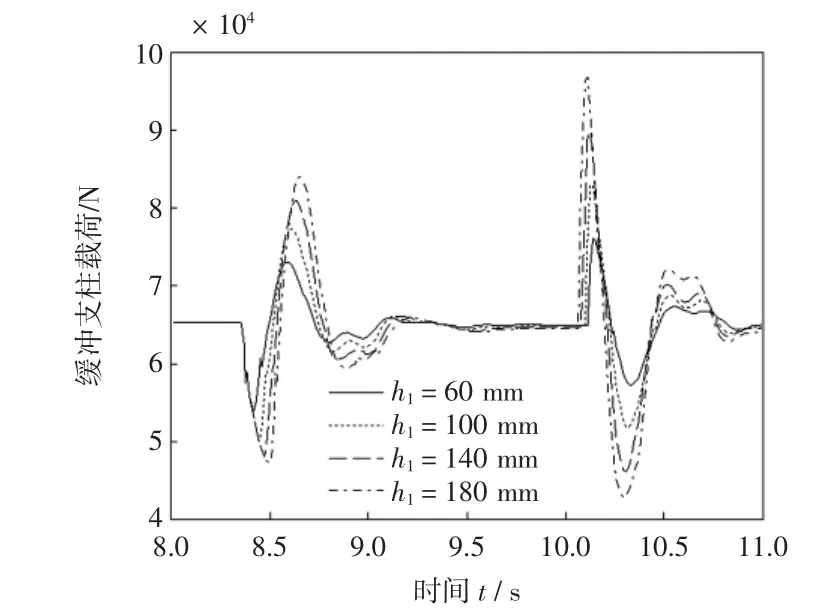
图8 A 型凹坑下前起落架缓冲支柱受力图Fig.8 Force on nose landing gear shock strut in Pit A

图9 不同凹坑深度下前起落架缓冲支柱载荷曲线Fig.9 Force on nose landing gear shock strut under different depth of pits
当考虑凹坑宽度对飞机前起落架缓冲支柱的影响时,只需研究B 型凹坑。如图10~图11 所示,当B型凹坑深度为h1=50 mm,宽度L=90 mm 时,飞机前起落架缓冲支柱受到的峰值载荷为8.09×104,且随着凹坑宽度的增加变化趋缓。当L <90 mm 时,缓冲支柱最大载荷随宽度增加而逐渐增大,当90≤L≤150 mm时,最大载荷随宽度增大而减小,而后缓慢增大。

图10 B 型凹坑下前起落架缓冲支柱受力图Fig.10 Force on nose landing gear shock strut in Pit B

图11 不同凹坑宽度下前起落架缓冲支柱载荷曲线Fig.11 Maximum force on nose landing gear shock strut under different depth of pits
对于同类型凹坑,当牵引系统出现故障时,为了更好地判断故障原因,不妨将两种情况在同一类型凹坑工况下进行峰值比较。如图12 所示,当牵引车和主机轮都经过B 型凹坑,凹坑深度一定(h1=15 mm)、牵引车匀速(5 km/h)牵引飞机时,分别得到主机轮和牵引车经过凹坑时前起落架缓冲支柱的峰值载荷,对比图6可以发现,牵引车经过凹坑时前起落架受到的载荷要大于主机轮经过凹坑时受到的载荷。
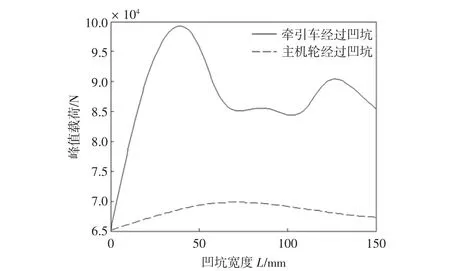
图12 同类型凹坑前起落架缓冲支柱载荷曲线Fig.12 Force on nose landing gear shock strut in same pit
3 结语
基于SolidWorks 和Adams 软件,建立了无杆牵引车-飞机系统,对两种不同凹坑类型下飞机前起落架的缓冲支柱进行了研究。结果表明:由于受到凹坑边缘对牵引车轮胎或者主起落架轮胎位移的突变影响,对于A 型凹坑,前起落架缓冲支柱受到的载荷随凹坑深度的增加而增大,且载荷变化趋缓;对于B 型凹坑,当深度不变时,随宽度增加,最大峰值载荷变化趋缓,但在凹坑宽度增大的过程中,前起落架的缓冲支柱载荷将达到峰值,然后峰值载荷逐渐减小,当减小到一定值后缓慢增加。对于同一类型凹坑,牵引车经过凹坑时前起落架缓冲支柱受到的载荷大于主机轮经过凹坑时前起落架受到的载荷。应尽量避免飞机牵引系统经过较大的凹陷或凸起路面,除了会受到最大幅值载荷的突变影响,还会受到小副值动载荷的影响,对牵引车抱轮装置的构件以及起落架的其他部件不利。后续研究可以针对主起落架和飞机横向牵引载荷,探讨牵引车的挡板牵引力变化规律,为牵引车抱轮装置对前起落架载荷裕度的设计提供理论参考。
