可渗透弹性悬臂梁式薄板横向绕流变形分析
2020-02-24高欣悦郝亚娟
高欣悦, 郝亚娟
(燕山大学理学院,秦皇岛 066004)
带孔的可渗透板壳在流固耦合问题中的应用十分广泛,如:在外国, Vinogradov等[1]研究了压缩激波与湍流边界层相互作用下可渗透板的传热;Gupta等[2]利用积分方程研究了水波与非对称非均匀渗透板的相互作用; Andronov等[3]得到了平面平行通道中稳定对称的分离流流过可渗透板的一般问题的精确解析解;Leontiev等[4]利用微分湍流模型对超音速气体流动中可渗透壁面的边界层进行了数值研究。在中国,白象忠课题组采用拉格朗日-欧拉法研究了可渗透球壳的流固耦合问题,给出了在小雷诺数的情况下渗透球壳在黏性流体中的位移解及内力解,分析了渗透参数和流速对壳体的影响[5],之后又采用该方法在考虑了壳的切向力和法向力的情况下,给出了壳的位移和流体压力的计算方法且分析了渗透参数对壳的变形、压力的影响[6];丁冠乔等[7]应用数值分析方法研究了雷诺数为200的多孔双圆柱的渗透率对其流场的影响;Ai等[8]提出了一种耦合各向异性渗透率的弹性薄板和饱和多孔弹性地基相互作用问题的BEM-ALEM方法。
现假设可渗透弹性薄板的孔很小且均匀分布,不会对其弯曲刚度及外部流场产生影响,不考虑孔造成的阻力。采用相容拉格朗日-欧拉法,求解可渗透弹性悬臂梁式薄板在理想流体绕流作用下的变形与应力,通过具体的算例,分析板的几何尺寸、渗透参数和流体流速对板的变形与应力的影响。
1 基本方程的建立
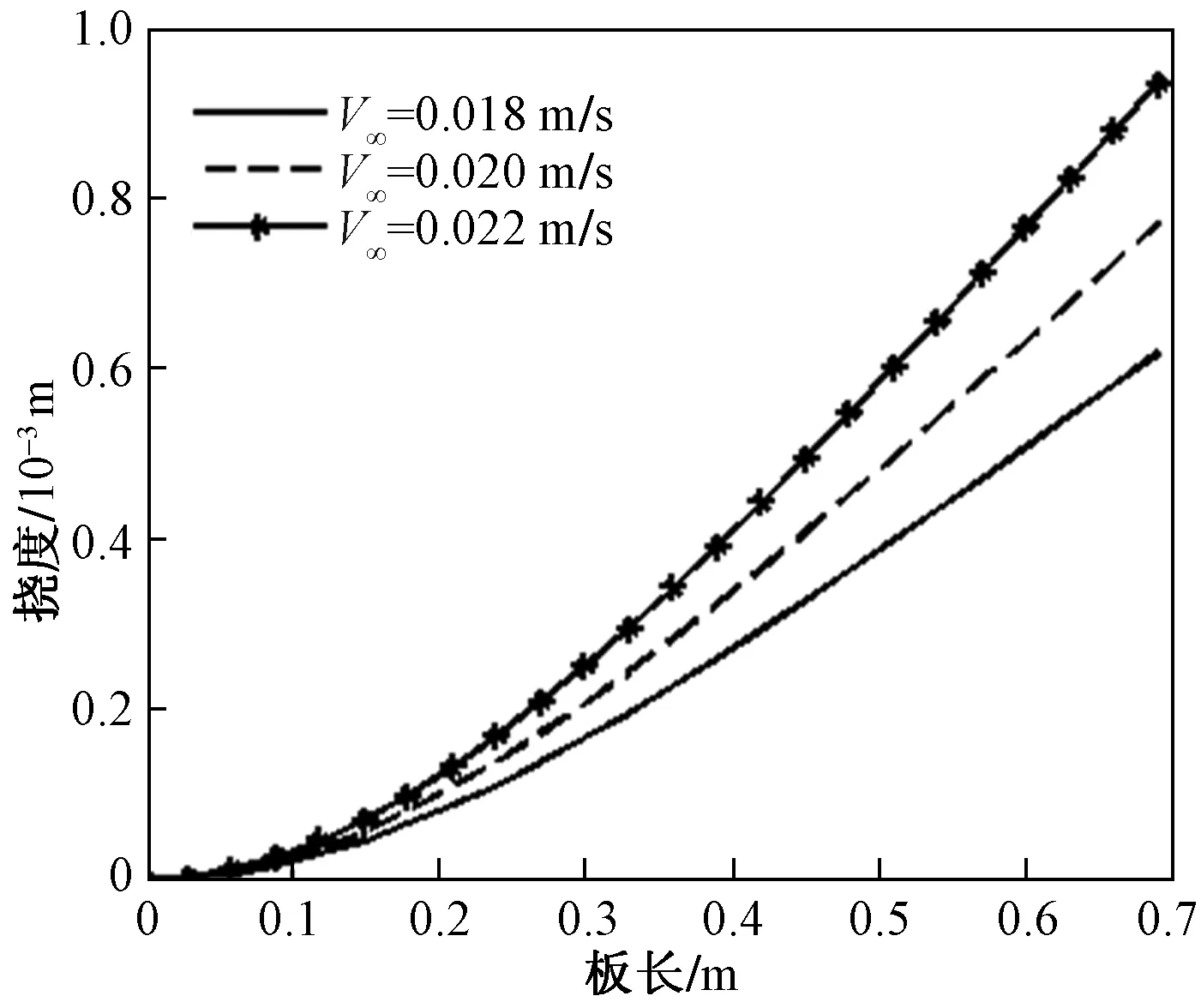
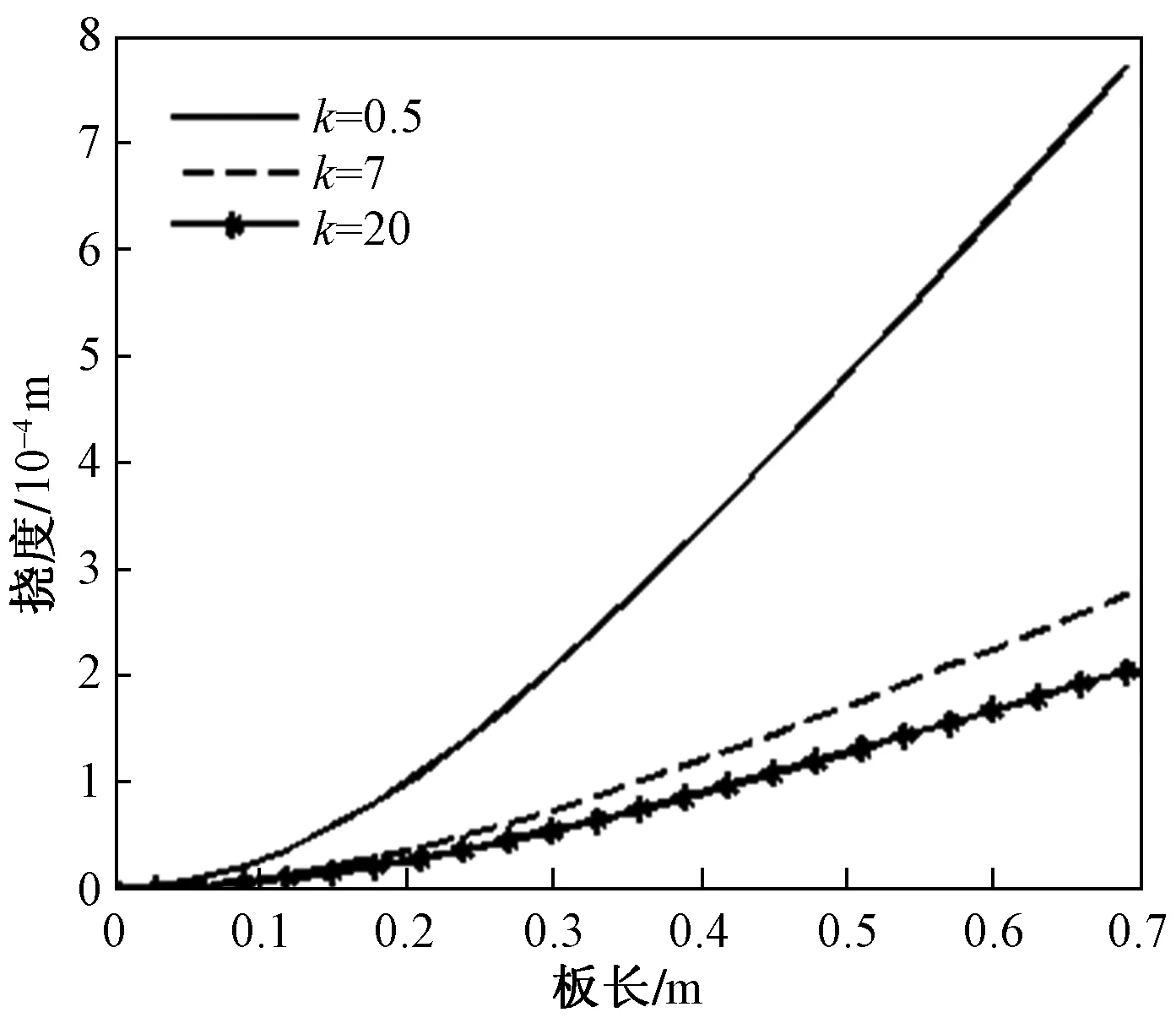
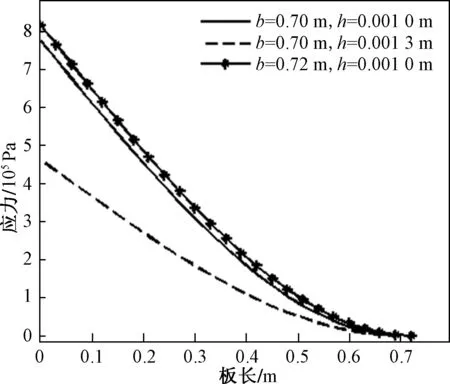
如图1所示,长度为b,厚度为h的可渗透弹性梁式薄板(-∞ y=0边固定: v(y)=w(y)=∂w(y)/∂y=0 (1) y=b边自由: N22(y)=Q2(y)=M22(y)=0 (2) 式中:v、w分别为薄板位移矢量在y轴和z轴上的投影,薄板发生小变形则位移矢量v(y)可以忽略不计;N22、Q2、M22分别为薄板发生小变形后作用于中面单位宽度上的拉压力、横向剪力和弯矩。在薄板变形的过程中,认为中面具有不可延伸性。 图1 悬臂梁式板绕流示意Fig.1 The cantilever beam-plate in a cross-flow 流体运动的速度势φ满足: (3) 流体运动的边界条件为 φ=V∞z,z→∞ (4) 接触面的运动学方程为[10] (5) 接触面的动力学方程为[10] (6) 式(6)中:Zi(i=2,3)为流体对薄板作用力在y轴和z轴上的投影;pi为薄板的阻滞压力。 悬臂薄板表面的线性关系式为[10] (7) 式(7)中:ρ为流体的密度;t为时间。 (8) 式(8)中:D=Eh3/12[1-ν2]为薄板的弯曲刚度,其中,E为薄板的弹性模量;ν为泊松比。 当薄板为刚性时,变形w1=0。薄板变形前流体运动的势函数为φ1,压力为p1,引起薄板弯曲的流体运动的势函数为φ2,压力为p2,薄板弯曲时产生的挠度w2,则有: p=p1+p2,φ=φ1+φ2,w=w2 (9) 将式(9)代入式(3)~式(5)和式(8)中,得: (10) φ1=V∞z,z→∞ (11) (12) (13) φ2=0,z→∞ (14) (15) (16) 式(16)为横向绕流条件下薄板发生小变形时的微分方程。由于弹性薄板发生小变形时势函数φ2和压力p2都很小,故在式(15)和式(16)中舍去了较小量∂p2/∂z、∂φ2/∂y和∂2φ2/∂z2。 设满足边界条件的挠度函数为[9] (17) 式(17)中:A为待定常数。 横向绕流薄板的流体势函数为[11] (18) 式(18)中:W=z2-y2+b2。 将式(18)代入式(10)得 (19) 当z=0时有: (20) 设势函数φ2为[11] (21) 式(21)中:B为待定常数。 则由式(13)知,当z=0时得: (22) 当y=0时阻滞压力为 (23) 由式(20)可知,当y=b/4和y=b/2时的压力分别为[11] (24) (25) 将x=1代入式(25)得f(x)=-7/15,故可估算出y=b时的阻滞压力为 (26) 采用线性渗透关系式[12]: (27) (28) 将式(23)和式(26)代入式(28),得: (29) 将式(17)、式(20)、式(22)和式(29)代入式(16)得: (30) 将式(30)的左右两边在y0=b/2处进行泰勒展开,并令两端的常数项和一次项相等,得: (31) (32) 联立式(31)和式(32),得: (33) (34) 由此,可以确定挠度w的表达式。 薄板表面应力分量σy的表达式为 (35) 设基本参数为:流体密度ρ∞=103kg/m3,板长b=0.7 m,板厚h=0.001 m,压力p∞=105Pa,流体速度V∞=0.02 m/s,渗透参数k=0.5,薄板的弹性模量E=200×109Pa,泊松比ν=0.5。 图2~图4分别是考虑流体的流速不同、板的几何尺寸和渗透参数不同时,板的w-y曲线。 图2 不同流速的w-y曲线Fig.2 w-y curves of different velocities 图3 不同几何尺寸的w-y曲线Fig.3 w-y curves of different geometric sizes 图4 不同渗透参数的w-y曲线Fig.4 w-y curves of different permeability parameters 由图2、图3可以发现,薄板的板长、流体的流速与薄板变形程度成正比,即随着板长与流速的增大,薄板变形程度增大;而薄板的板厚与变形程度成反比。由图4可知,薄板的渗透参数越大,挠度越小,也就是渗透情况越好,变形越小,薄板的渗透参数与变形程度成反比。 图5~图7分别是考虑流体的流速不同、板的几何尺寸和渗透参数不同时,板的σy-y曲线。 图5 不同流速的σy-y曲线Fig.5 σy-y curves of different velocities 图6 不同几何尺寸的σy-y曲线Fig.6 σy-y curves of different geometric sizes 图7 不同渗透参数的σy-y曲线Fig.7 σy-y curves of different permeability parameters 由图5、图6可知,应力数值由固定端沿y轴单调递减至0,应力曲线越临近固定端梯度越大。薄板的板长、流体的流速与应力数值下降速度成正比,即板长越长、流速越快,应力数值下降速度越快;薄板的板厚与曲线梯度成反比。由图7可知,薄板的渗透参数越大,应力越小,也就是渗透情况越好,应力数值下降速度越慢,薄板的渗透参数与应力数值下降速度成反比。 (1)采用相容拉格朗日-欧拉法求解理想流体绕流可渗透弹性悬臂梁式薄板的流固耦合问题,得出弹性体的变形、应力表达式。 (2)给出了流体流速、板的几何尺寸、渗透参数的变化对可渗透梁式板的挠度及应力的影响和变化趋势。 (3)可以为进一步研究理想流体绕流可渗透弹性体的流固耦合问题奠定基础。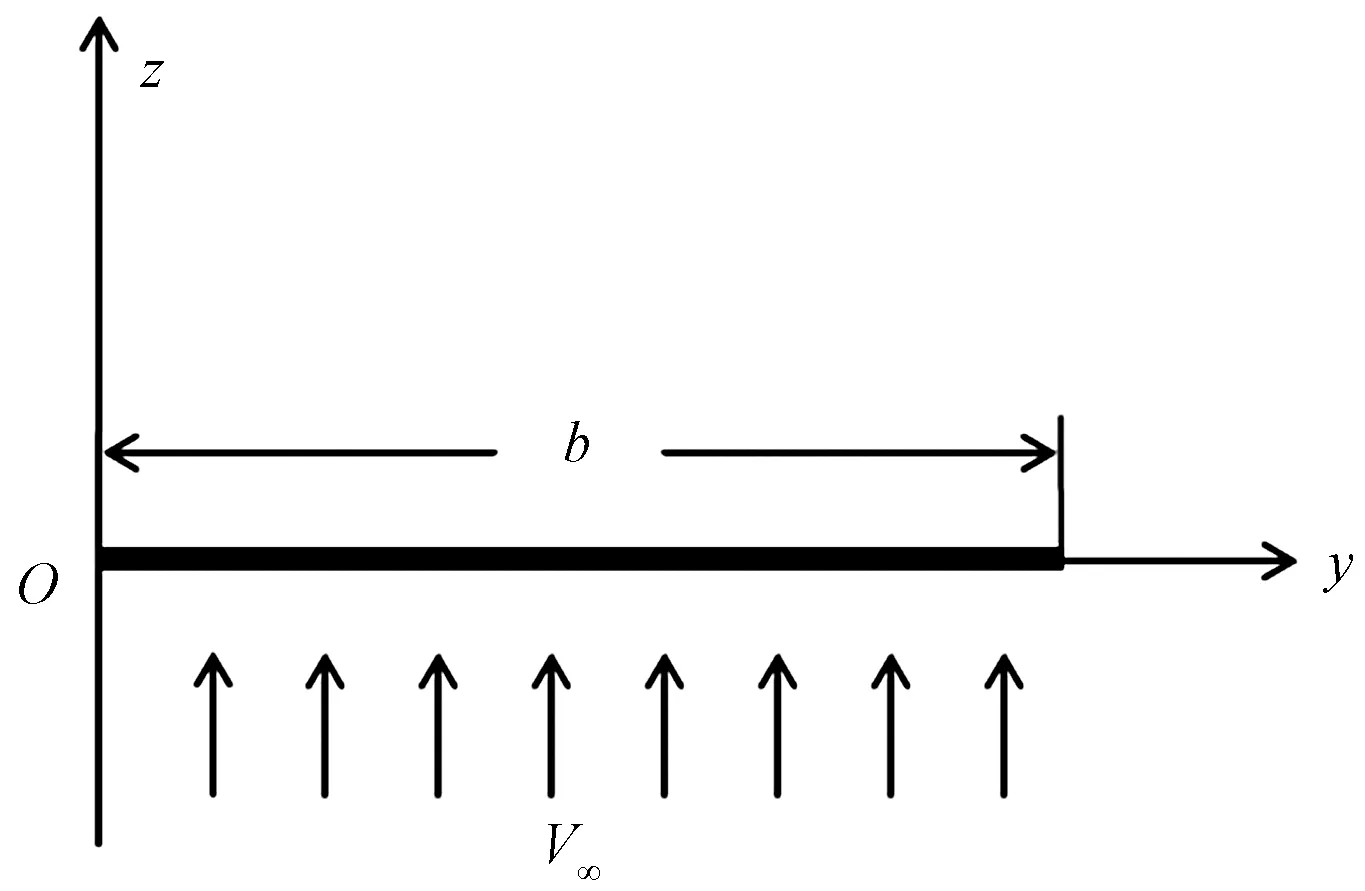



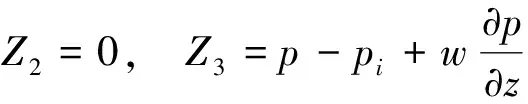
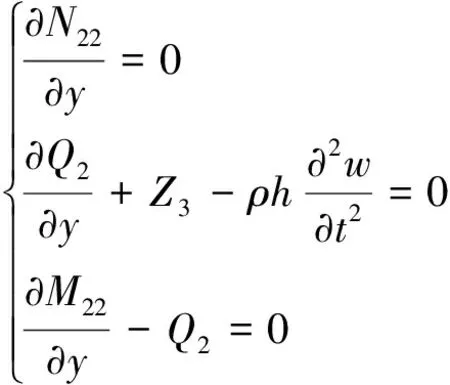
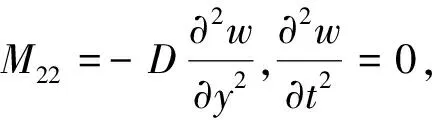




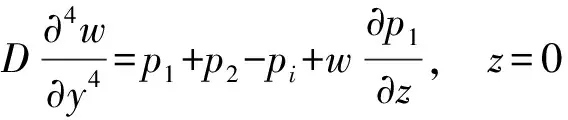
2 基本方程的求解
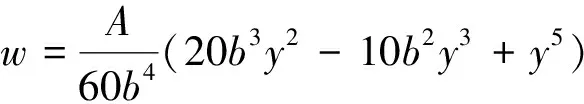

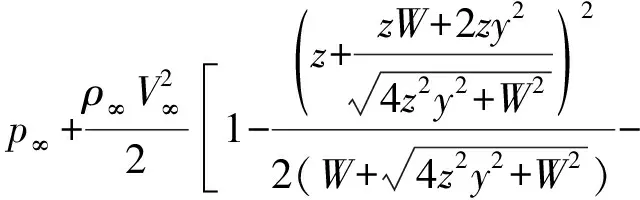
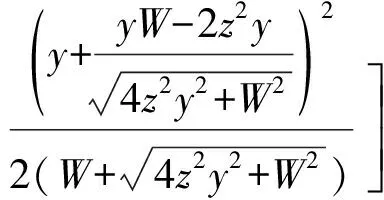


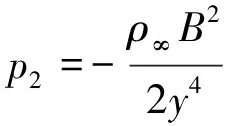


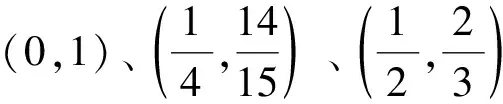
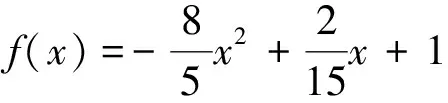


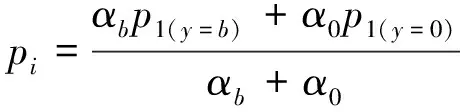
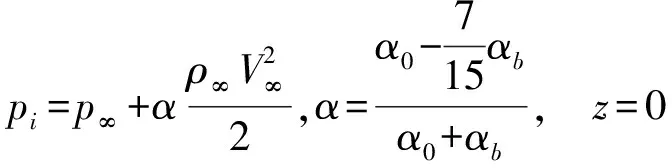

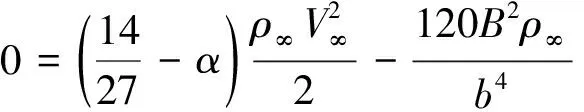



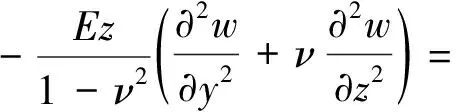

3 算例分析



4 结论
