重力卫星时变重力场去相关滤波算法的参数选择

崔立鲁， 唐兴友， 邹正波， 宋 哲， 许文超

(1.成都大学建筑与土木工程学院,成都 610106；2.武汉大学测绘学院,武汉 430079；3.中国地震局地震研究所,地震大地测量重点实验室,武汉 430071)

GRACE(gravity recovery and climate experiment)卫星重力计划是由美国宇航局和德国空间飞行中心联合实施的,该卫星计划的主要目的是实现对地球表层质量变化和重新分布的连续监测,目前已经被广泛地运用于陆地水储量变化、冰川均衡调整、全球海平面变化、区域地壳构造形变等领域[1-2]。

由于GRACE卫星轨道误差、仪器测量误差、卫星姿态测量误差等和潮汐或非潮汐引起的海洋和大气质量变化对地球重力场模型等综合影响,直接利用GRACE月重力场球谐系数反演地表质量变化,会出现明显的南北方向上条带误差。中外学者一般采用滤波算法对这些误差进行削弱。根据滤波算法原理的不同,主要可以分为两类[3]:①空间类滤波,即引入滤波因子以降低高阶次项在数据处理中所占权重,从而达到减小条带误差的目的。该类方法主要有高斯滤波[4]、Fan滤波[5]、维纳滤波[6]等；但是空间类滤波存在着一定的局限性,即随着滤波半径越大,条带误差的抑制效果越好,但是空间分辨率的损失程度也越大；②去相关滤波,是利用滑动窗口多项式对相关误差进行拟合,进而将去从球谐系数中消除,从而达到去相关的目的[7]。Duan等[8]利用球谐系数的标准差以约束条件对去相关滤波进行了改进,有效地提高了去相关效果；卢飞等[9]针对数据序列两端无法进行去相关处理的问题,采用非中心点窗口拟合法,取得了良好的效果；詹金刚等[10]提出了反向延拓技术扩展了去相关滤波的处理范围,提高了处理的效率。

根据去相关滤波算法的基本原理可知,算法中滤波参数的设置对于去相关效果有非常重要的作用,但是目前尚未有一个公认的定论[11]。鉴于此,本文通过对滤波参数的设置,详细分析了滤波参数的变化对去相关滤波效果的影响,并且着重地研究重力场模型球谐系数滤波起算阶数、滑动窗口宽度和拟合多项式阶数三种滤波参数对条带误差处理效果的影响,给出滤波参数设置的建议值。

1 陆地水储量变化反演原理

利用GRACE时变重力场球谐系数反演陆地水储量变化的表达式为[5]

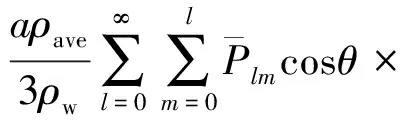
(1)

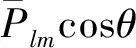
但是由于重力场模型球谐系数高阶项之间存在的相关误差影响,由GRACE月重力场反演得到的陆地水储量变化结果会呈现出明显的南北条带误差,如图1所示。因此必须采用相应算法对模型中的球谐系数进行去相关处理。

图1 未经处理的反演结果Fig.1 The inversion results without being pre-processed

2 去相关滤波算法

根据文献[7]的研究表明,当次数大于8时,球谐系数的阶次之间表现出显著的相关性；而阶次数均小于8时,阶次项之间的相关性并不明显,可以忽略不计。同时,对奇数项和偶数项分别进行去相关滤波。因此,滤波算例如下[4]。

当滑动窗口取7时,利用ΔCl-6,m、ΔCl-4,m、ΔCl-2,m、ΔCl,m、ΔCl+2,m、ΔCl+4,m、ΔCl+6,m这七项进行三次多项式拟合,拟合得到的结果即为相关误差：

ΔCm(l)=a0+a1l+a2l2+a3l3

(2)

3 实验与分析

3.1 数据说明

实验数据来源于美国德克萨斯大学空间研究中心(center for space research of texas university in austin, CSR)发布的RL05版本Level-2的时变重力场模型,2003年1月—2015年12月共计156个月,模型截断至60阶。为了直观地比较实验结果,根据文献[12—18]的球谐系数法,利用实验得到的球谐系数反演全球陆地水储量变化作为验证参数选取结果的依据。

3.2 实验结果分析

为了验证三个滤波参数对去相关处理效果的影响,设置了三个不同的实验,分别是：①滤波算法起算阶数为15阶、20阶、25阶和30阶；②滑动窗口宽度为5、7、9、11；③多项式拟合阶数为2,、3、4、5阶。

3.2.1 不同的滤波起算阶数

为了更好地体现不同起算阶数对反演结果的影响,本项实验中将多项式拟合阶数设置为3,滑动窗口宽度为7,计算结果如图2所示。根据图2结果可知,去相关滤波算法对条带误差有着明显的抑制作用,其中高纬度地区得到了明显的改善,但是低纬度地区的误差还是很明显。由图2可知,4个不同起算阶数所得到的反演结果大体上没有太大变化,但是在高纬度的局部区域,发现条带误差在明显地增强,这说明高阶次球谐系数相对于低阶次项误差所占的比重要大,而低阶次项正常信号为主,因此在实际数据处理中,起算阶数不能太小,这样会导致正常信号的丢失,严重影响GRACE反演结果。但是起算阶数多高,则会将带入高阶次项中的噪声影响,不利于正常信号的判别。因此,建议起算阶数为15阶较为适宜。

3.2.2 不同的滑动窗口宽度

根据实验①的结论,本项实验中球谐系数的起算阶数定为15阶,多项式拟合阶数设为3,实验结果见图3所示。由图3可知,随着滑动窗口宽度从5变为11,条带误差呈现出由低纬度地区向高纬度地区蔓延的趋势,且误差在逐渐增大,这说明滑动窗口宽度的增加并没有提升去相关效果,反而使去相关效果越来越差。这主要是窗口宽度的增加削弱了球谐系数之间的相关性。根据分析结果,滑动窗口宽度设为5较为合适。

根据文献[10]的分析,球谐系数的相关性主要体现在高阶次项,而在低阶次项中相关性并没有那么明显,因此在设计滑动窗口宽度时,针对高阶次项和低阶次项的不同特点进行区别对待,可以在低阶次项采用较大的滑动窗口宽度,而高阶次项处理时采用滑动窗口宽度较小的去相关滤波。

3.2.3 不同的多项式拟合阶数

根据实验①和实验②的结论,本项实验中球谐系数的起算阶数定为15阶,滑动窗口宽度设为5,实验结果如图4所示。由图4可知,随着多项式拟合阶数增加,去相关滤波算法的处理效果得到了一定的改善。但是当拟合阶数增加到5阶时,其去相关效果与4阶的时候差别不大。因为随着阶数增加,数学模型会变得较为复杂,同时运算效率会大大下降,但是得到的结果却没有明显的改善,所以建议采取多项式拟合阶数设置为4阶。

图4 不同多项式拟合阶数对去相关滤波结果的影响Fig.4 The influence of different order of fitting polynomial on the result of de-correlation filtering

4 结论

利用基于滑动窗口的去相关滤波算法消除或削弱由GRACE时变重力场高阶次项相关性引起的南北条带误差是目前重力场数据预处理阶段的常用方法。在利用该滤波算法进行数据处理时,需要对算法中的三个参数进行设置,分别是起算阶数、滑动窗口宽度和多项式拟合阶数。为了详细研究三个参数对去相关处理效果的影响,设计了大量的数值实验并进行了对比和分析。根据实验结果可知,滑动窗口去相关滤波算法对高纬度地区的条带误差有着明显的削弱作用,但是对低纬度地区的效果不是很有效；在设定三个参数数值的时候主要考虑的是高、低阶次项去相关性的强度大小,同时还要考虑整个算法的运算效率。但是研究还存在一些不足,例如在滑动窗口宽度设置时需要分别考虑高阶次项和低阶次项的相关性强度大小,研究滑动窗口宽度可变的去相关滤波算法等。