中美中小学生科学推理能力发展的差异研究

周少娜 Bao Lei 陈佐满 何雨泽

在1909年，美国著名实用主义教育家杜威(Dewey)在美国科学进步联合会的发言中首次提出科学教育的目的：让学生学会大量的知识，并要求学生学习科学研究的过程和科学方法。国际科学教育开始注重和培养学生的科学方法和思维，特别是培养学生的科学推理(Scientific Reasoning)能力。2018年1月16日，教育部印发了《普通高中课程标准(2017年版)》，指明了各个学科核心素养。在普通高中物理课程标准中，科学思维与其他三个维度(物理观念、科学探究、科学态度与责任)被确定为四大物理学科核心要素。[1]我国课标首次突显科学思维的重要性，并且明确了其四要素：模型建构、科学推理、科学论证和质疑创新。从课程标准的角度，学生的科学推理能力已成为普通高中生应该具备的基本能力之一。

研究者把科学推理分为六个维度，包括守恒推理(Conservation Reasoning)、比例推理(Proportional Reasoning)、控制变量(Control of Variables)、概率推理(Probability Reasoning)、相关推理(Correlation Reasoning)和假设演绎推理(Hypothetico-deductive Reasoning )。根据皮亚杰儿童认知发展理论，科学推理能力六个子推理类型的发展一般经过具体运算、过渡阶段和形式运算等几个不同的过程，学生科学推理能力的发展是一个复杂过程。通过对国内外中学生的科学推理能力现状及发展的研究的综述，并通过实证调查以获取中美两国学生的科学推理能力的共性和差异。

一、研究综述

皮亚杰在认知理论中首次提出科学推理的概念，在国际上掀起了关于科学推理能力的研究热潮，至今科学推理能力仍是国际科学教育研究的重要领域。为了解国内外学生科学推理能力的发展情况，从以下两个角度对国内外的相关文献进行梳理：学生科学推理能力的总体发展情况和科学推理能力各个子维度的发展平衡性问题。

国外众多相关研究表明，学生的科学推理能力的整体发展水平不理想，只有少数学生达到形式运算水平。1977年，Karplus等人对13—15岁的学生进行科学推理能力水平的研究，结果表明仅有25%的学生处于形式运算水平。[2]1985年和1992年，Shemesh等人研究发现，尽管7—12年级的学生的科学推理形式运算能力比例随年龄的增长而递增，但仍有50%的学生处于具体运算推理阶段。[3][4]1989年，Bitner对学生的科学推理能力进行研究，发现6—10年级学生尚未达到形式运算推理水平。[5]2000年，Vass等人的研究表明大学毕业生仍有很多被试者在比例推理、概率推理和关系推理等科学推理维度仍达不到形式运算水平。[6]

尽管学生的科学推理能力的整体水平不尽如人意，但随着年级的增长和知识的积累，科学推理发展水平呈增长趋势。[7]这吻合皮亚杰的认知发展理论，当学生从具体形象思维过渡到抽象逻辑思维时，学生的科学推理发展水平也趋于成熟。Kuhn研究了9年级学生到60岁受访者的科学推理能力的层级，结果发现教育程度差异影响了受访者的科学推理能力水平，大学以上教育程度受访者的推理能力明显优于高中及以下教育程度的受访者。[8]

从学生科学推理能力的子维度来看，各个维度的发展是不均衡的，有些维度优先发展，有些维度则发展较慢。国外研究者根据不同的立足点，采用不同的科学推理能力测量工具，分别侧重科学推理能力的不同维度进行细致研究。如贝佛里奇认为科学研究中，比较重要的三个子维度是归纳推理、演绎推理和类比推理。[9]而Lawson等人认为科学推理有六个子维度，分别是守恒推理、比例推理、控制变量推理、概率推理、相关推理和假设演绎推理。[10]Hogan等人将科学推理分为类比式推理、对话式推理、分析式推理、推论式推理、整合式推理和评价式推理六个维度。[11]Driver等人将科学推理分为现象推理、关系推理和模型推理三个维度。[12]有学者研究了韩国初中生科学推理发展水平，研究结果显示出韩国初中生的比例推理和概率推理的形式运算水平发展相对较晚，而组合和关系推理的形式运算水平发展得相对较早。[13]而Bitner的研究则表明学生最迟发展的是关系推理和概率推理，这两个维度对学生来说最困难。[14]Hackling等人通过比较高中生和科学家的科学推理能力，发现高中生在重复测量实验和控制实验变量上，认知和处理能力方面表现较差，发展较慢。[15]郭玉英等对我国师范院校物理专业大学生进行科学推理能力研究，发现我国师范院校物理专业大学生的科学推理能力没有随年级增长而增长的趋势，认知水平处于“后形式运算”阶段的个体所占比例较低。[16]张轶炳等在宁夏大学开展大学生的科学推理能力研究，发现西部地区大学生科学推理各维度发展不平衡。[17]

国外不少研究者还关注不同教育因素对学生的科学推理能力发展的影响，如学习成绩[18][19][20]、前知识[21]、信息加工能力[22]、认知风格[23]、智商[24]、文化背景[25]、个体能力[26]、个性因素[27]等。国内研究者也进行了一些相应的研究，如李力舟等对甘南藏族地区和北京高一学生科学推理能力进行对比研究[28]；周思琪对不同地区的高一和高二学生的科学推理能力进行研究[29]。邢红军[30]、谈学婕[31]、梁美怡[32]、艾彤[33]、杨燕[34]等对学生的科学推理能力与其他学习能力进行相关性研究。

二、问题的提出与方法

(一)问题的提出

2009年，美国俄亥俄州立大学包雷教授在《自然》杂志发表了一项重要的研究，研究表明：尽管中国大一学生的学科知识水平远比美国大一学生高，但是两国学生的科学推理能力不相上下，即学生科学推理能力与物理知识之间没有相关性。[35]这从侧面反映出我国学生在科学知识和科学推理能力上发展不平衡。但该研究并未对中美学生在科学推理能力不同维度的表现进行深入地剖析。因此，本研究以中美两国的中小学生为研究对象，对中美学生科学推理能力的发展以及各维度的表现进行差异性研究，具体围绕以下两个研究问题：

(1)中美两国中小学生科学推理能力的发展是否存在差异？

(2)中美两国中小学生科学推理能力不同维度的发展是否存在差异？

(二)研究方法

本研究采用美国加利福尼亚大学Lawson教授团队开发的科学推理测量表(Lawson’s Classroom Test of Scientific Reasoning，简称LCTSR)。[36]2000年修改过的LCTSR量表在国际物理教育界颇受欢迎，使用广泛。LCTSR测试量表由12组二元题目构成，共24小题。每组二元题包含两小题，第一小题为决策题；第二小题为解释题，即对前一题选项的解释。整份量表分为六个维度：守恒推理(Q1—Q4)，比例推理(Q5—Q8)，控制变量推理(Q9—Q14)，概率推理(Q15—Q18) ，相关推理(Q19—Q20)，假设演绎推理(Q21—Q24)。

(三)研究对象

研究对象为中国和美国的中小学生。考虑到小学五年级开始，学生具有较好的阅读和理解能力，因此选择五年级到高中三年级(5—12年级)的学生作为研究对象。中美的测试对象一共有8549人，其中，中国学生6328人，美国学生2221人。中美两国研究对象人数的年级分布如表1所示。

表1中美两国研究对象人数的年级分布

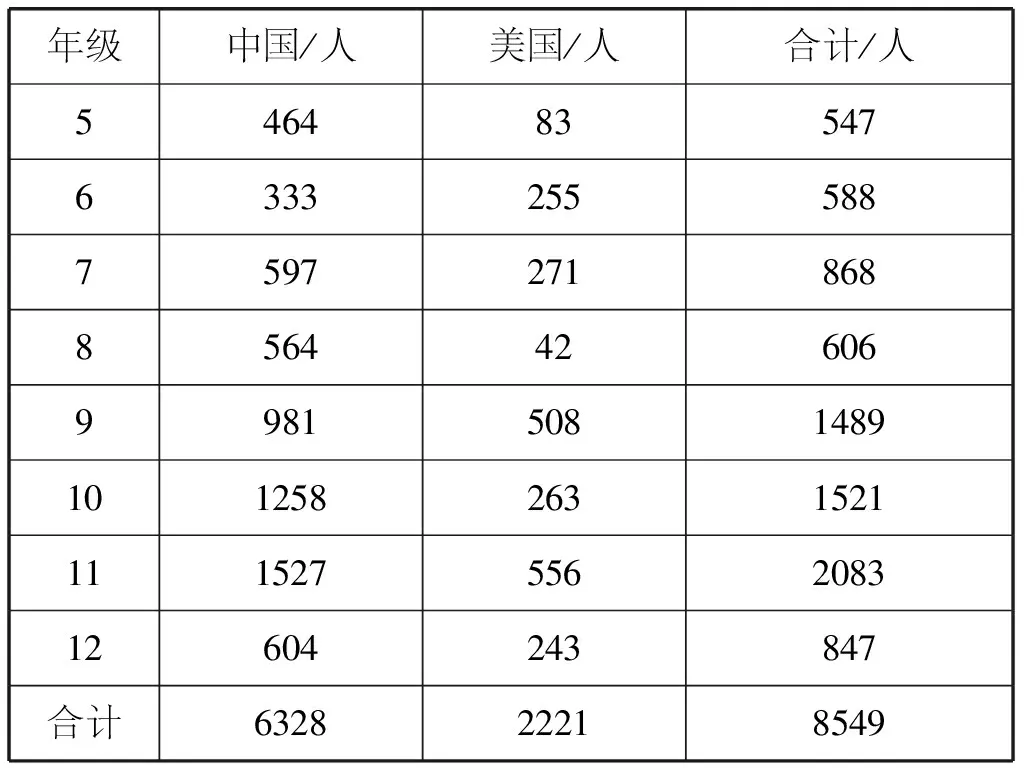
年级中国/人美国/人合计/人54648354763332555887597271868856442606998150814891012582631521111527556208312604243847合计632822218549

三、研究分析及结果

分析采用Lawson提出的评分方式：在二元题中，有且只有当两道题同时答对，才得分；否则，只要有一题答错，不给分。Lawson认为如果学生决策题做对，解释题做错，那么该学生极有可能是猜测对了决策题，此时不应该获得相应的分数；而如果学生决策题做错，解释题做对，则解释题的选择是不符合科学逻辑的。

(一)中美学生的科学推理能力的总体水平不高，但不同年级差异显著

LCTSR测试结果如表2所示，包括中美两国参与测试的各年级学生人数、平均分、正确率、标准差和t检验的p值。由表2可见，两国学生的科学推理能力的整体水平不高，除了中国的高三(12年级)学生的平均分超过及格线(总分12分，及格线为7.2分)外，其他年级学生的平均分均不能达到及格水平。中国高三(12年级)学生比高二(11年级)学生科学推理能力正确率高出约15%，t检验显示两个年级的表现差异极其显著(P<0.001)，这说明在高三的总复习中学生的科学推理能力也可得到相应提高。从纵向看，随着年级增长，中美两国学生科学推理能力均呈递增趋势。尽管两国学生总体科学推理能力有待加强，但随着学科知识的积累和能力的培养，思维也不断发展，故科学推理能力的发展水平也不断提高。

从横向比较，t检验显示，除了中美两国9年级学生的科学推理能力不存在显著差异(P=0.42)外，中美其他年级学生的科学推理能力水平差异(Ps<0.05)均具有统计意义。根据学生智力发展水平，将5—12年级的学生分为低年级、中年级和高年级三个年级段，分别为5—6年级(G5—6)、7—9年级(G7—9)、10—12年级(G10—12)，对应中国小学、初中和高中年段。将三个年级段的中美学生在科学推理能力测试的平均分绘制成柱状图，如图1所示。由图1直观可见，美国低年级学生(G5—6)在科学推理能力测试的表现均明显优于中国低年级学生(P<0.001)；而中国高年级学生(G10—12)的科学推理能力均显著优于美国高年级学生(P<0.001)；中美两国在7—9年级的学生整体表现差异不大(P=0.42)。

表2中美两国各年级学生在LCTSR测试中的表现

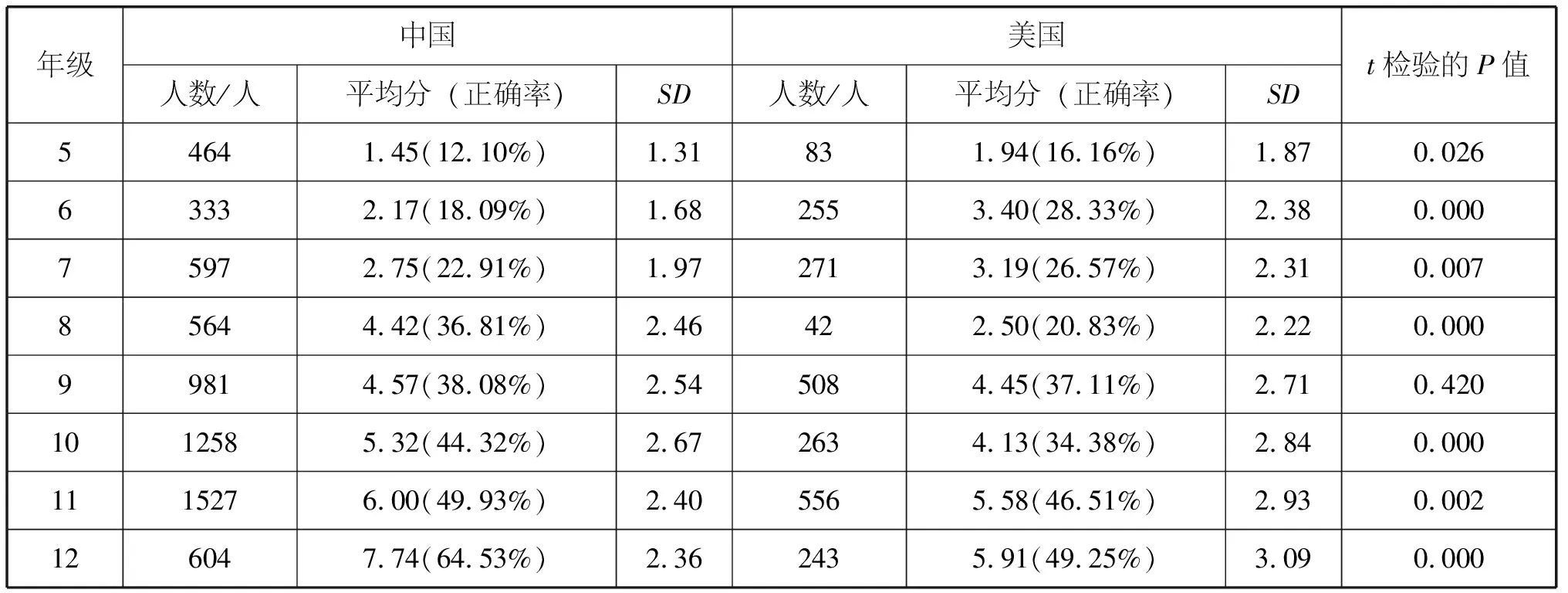
年级中国美国人数/人平均分(正确率)SD人数/人平均分(正确率)SDt检验的P值54641.45(12.10%)1.31831.94(16.16%)1.870.02663332.17(18.09%)1.682553.40(28.33%)2.380.00075972.75(22.91%)1.972713.19(26.57%)2.310.00785644.42(36.81%)2.46422.50(20.83%)2.220.00099814.57(38.08%)2.545084.45(37.11%)2.710.4201012585.32(44.32%)2.672634.13(34.38%)2.840.0001115276.00(49.93%)2.405565.58(46.51%)2.930.002126047.74(64.53%)2.362435.91(49.25%)3.090.000

图1 不同年级段的中美学生的平均分

中美两国学生在科学推理能力测试上的差异并非一成不变，其差异的显著性和方向性随年级段而发生变化。这也说明，长期讨论的中美两国不同的教育理念和教学方法孰优孰劣的问题并没有唯一确定的答案。美国的基础科学教育注重科学素质、科学探究、科学思维、科学技术与社会的关系，提倡小组合作—探究的学习方式，其低年级的学生思维活跃，科学推理水平得到了发展。而目前中国的科学教育受应试教育影响，以学生为主体的学习方式尚未盛行，学生科学素养和推理能力有待加强。而随着年级段增长，中国学校课程设置了更多科学相关课程，如物理、化学、生物，学生科学知识得到了大量积累，科学推理技能得到显著提升。

(二)中美学生在不同科学推理维度的差异比较

1.中美学生在不同维度的总体比较

将中美两国全体被试学生在科学推理能力测试的表现按照守恒推理、比例推理、控制变量推理、概率推理、相关推理和假设演绎推理六个子维度分类。采用雷达图(如图2)直观描述中美两国学生在科学推理不同维度上的表现。整个雷达图为正六角形，每一个角表征科学推理能力的一个维度。中美两国学生的科学推理能力均为不规则六边形，角离中心点的距离为该维度的正确率。

图2 中美学生在科学推理不同维度的正确率比较

根据雷达图，从纵向来看，中国学生的守恒推理维度距雷达图中心最远，表现最佳；其次是比例推理；另外，控制变量推理、概率推理、相关推理和假设演绎推理四个维度相对靠近雷达图中心，最差的是假设演绎推理和控制变量推理。美国学生守恒推理和概率推理两个维度据雷达图中心最远，表现最佳；其次是相关推理；而比例推理、控制变量推理和假设演绎推理三个维度距雷达图中心较近，说明美国学生在这三个维度表现不尽如人意。

从横向来看，t检验结果显示中美两国学生在科学推理能力六个子维度上均呈显著性差异(Ps<0.01)。结合图2可见，中国学生在守恒推理、比例推理、控制变量推理和假设演绎推理的维度上优于美国学生。尤其是比例推理，中国学生的平均正确率(44.24%)显著高于美国学生(20.55%)，呈极其显著差异(P<0.001)。而美国学生在概率和相关推理显著优于中国学生，特别是概率推理。

2.中美不同年级段学生在不同科学推理维度的差异比较

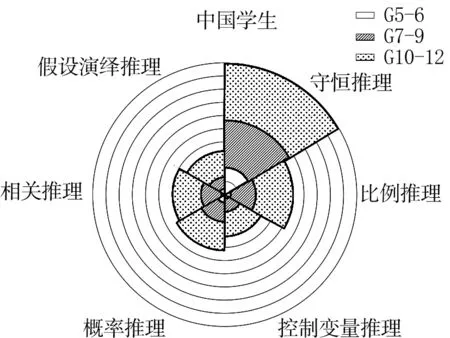
为了进一步研究中美不同年级段学生在科学推理能力六个维度上的差异，将两国学生各分为5—6年级(G5—6)、7—9年级(G7—9)、10—12年级(G10—12)三个年级段进行分析。采用极区图(即南丁格尔玫瑰图)表示中美两国不同年级段学生在科学推理能力不同维度上的表现(如图3)。极区图包含两个基本量，一个是扇形的角度，表示分类；一个是扇形的半径，表示各个类别的结果(可以是数值或百分比)。如果某个类别中有二次分类，将扇形半径根据分类数值比例进行横向切割，则各个切割环形宽度表示子类别的结果。图3(a)和(b)中美两国的坐标圈数相等，一周360°共表示科学推理能力的六个维度，每60°表示科学推理能力的一个维度。图中扇形半径表示学生在各个维度的平均得分，半径越大表示学生平均得分越高。根据极区图，通过比较同一扇形半径上不同图案所占线段大小，可分析不同年级段学生的科学推理能力某一维度的表现差异；同时，比较图3(a)和(b)某一科学推理维度相同图案的线段大小，可分析中国学生和美国学生相同科学推理维度相同年级段的表现差异。

(a)

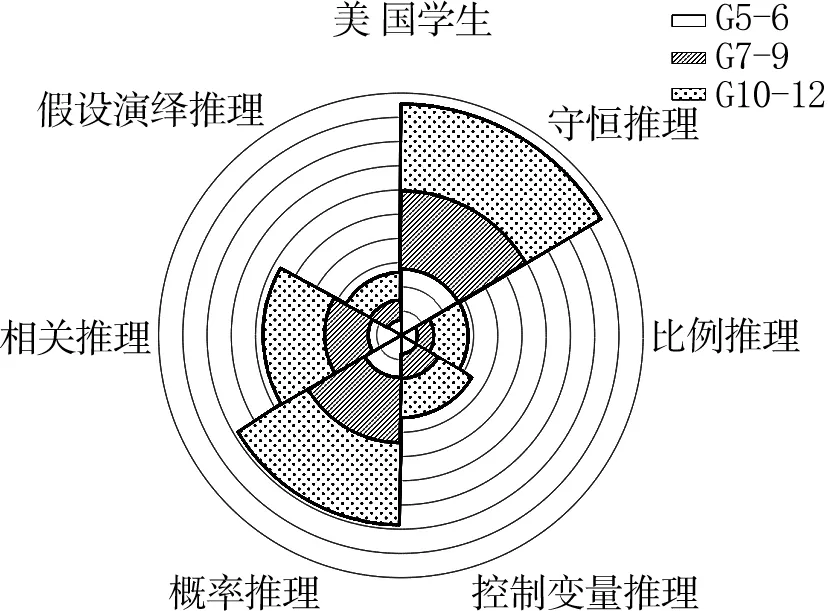
(b)图3 中美两国学生各年级段在科学推理能力不同维度的表现

从纵向分析，极区图各个扇形由里及外不同图案的径向宽度逐渐增大，说明中美两国学生从低年段到高年段，科学推理能力六个维度均呈上升趋势。中国G5—6年级段学生，除了守恒推理外，其他五个维度图案径向宽度占比非常小，说明在科学推理能力测试中，中国低年级段学生在多个科学推理维度上表现不佳。特别是相关推理，仅有0.05%的G5—6年级段学生作出正确判断。中国G7—9年级段的学生在不同的科学推理维度均有一定起色，平均得分比G5—6年级段呈倍速增长。其中，比例推理和相关推理增幅最大。到G10—12年级段，中国学生在科学推理能力各维度的测试中均有明显增长。美国相同年级段学生在不同科学推理能力维度的表现不均衡。

从横向分析，中美两国各个年级段学生在科学推理测试中各个维度的表现差异明显。G5—6年级段，t检验显示中美两国学生在科学推理六个子维度的表现均具有显著性差异(Ps<0.05)，美国G5—6年级段学生在各个科学推理维度的表现均明显优于中国学生，尤其是在控制变量推理、概率推理和相关推理上，正确率均高出中国学生超一倍。G7—9年级段，中美两国学生在控制变量推理和假设演绎推理两个维度上没有显著性差异(P=0.508和P=326)，而在守恒推理、比例推理、概率推理和相关推理四个维度均呈极其显著差异(Ps<0.01)。中国的G7—9年级段学生在守恒推理和比例推理上表现明显优于美国G7—9年级段学生，而在概率推理和相关推理上表现明显弱于美国G7—9年级段学生。G10—12年级段，中美两国学生在科学推理六个子维度的表现均具有极其显著差异(P<0.01)。美国G10—12年级段学生仍在概率推理和相关推理两个维度上保持明显优势。而中国G10—12年级段学生在守恒推理、比例推理、控制变量推理和假设演绎推理四个维度显著优于美国G10—12年级段学生。

四、思考

(一)对我国基础教育应保持教学自信

长期以来，西方以自主、探究式教学著称，而我国以传统讲授式或应试教育教学为主。而对于自主探究教学与传统讲授式教学孰是孰非、孰优孰劣的国际教育研究经久不衰。从本研究结果看，中国低年级段学生的科学推理能力落后于美国同年级段学生，但是在传统讲授式教学模式下，中国学生的科学推理能力水平在初中阶段赶上了美国学生，并在高中阶段超过美国学生。虽然中国传统讲授法被诟病，但同时我们也不可忽略一个事实：中国的基础教育水平正得到世界认同。2009年和2012年，在评价全球七十多个国家基础教育水平的PISA国际学生评估项目所进行的阅读、数学和科学的测试中，中国学生均排名第一。2013年，丹麦广播电台拍摄了一部纪录片——《丹麦九年级学生VS中国初三学生》，组织了一次关于阅读、数学、英语、创造力和团队能力的考试。结果，除了英语科目以外，中国学生在知识能力、创造力及团队合作能力的考试上全部获胜。在意识到传统讲授式教学缺点的同时，我们也应该对基础教育充满自信。中国的基础教育已经走在世界的前列，中国已经由原来的教育进口国开始转变为向世界输出教育经验。2014年，上海正式与英国启动中英数学教师交流项目，成为中英两国人文交流机制的重要组成部分。2016年7月，英国谢菲尔德汉勒姆大学的第三方评估报告将上海数学教育经验总结为“上海掌握教学模式”。上海教师的示范教学已经在英国中小学校引起教学变革，并帮助英国学生取得了学习进步，提升了英国学生对数学的热情，促进英国学生对教学的深度参与，增加英国学生的自信心和数学素养。

(二)教师需要审视科学思维能力的培养

科学思维是基于知识又高于知识的高阶思维，是思考和解决实际问题的技能源泉，是对世界的复杂性、整体性和多样性的全局把握。其实质是通过合理地处理各种科学思维方法之间的辩证关系，使其达到最优化，做到科学地、全面地观察问题和思考问题，得出解决问题的科学方法。根据《普通高中课程标准(2017年版)》，科学思维和推理被认定为各学科核心素养。如数学学科核心素养之一为逻辑推理，具体包括推理形式为归纳、类比的从特殊到一般的推理，推理形式为演绎的从一般到特殊的推理；化学学科核心素养包括证据推理与模型认识；生物和物理共同把科学思维作为学科核心素养之一。无论从科学思维的本质出发，还是从国家教育顶层设计的思路出发，科学思维均被放在相当重要的位置。

然而，从教育实际来看，培养科学思维的落地与实施并没有达到理想的目标。本研究测试结果从侧面反映出我国学生科学思维水平有待加强。我国学生的科学推理能力并没有随着知识的积累而发展到相应的水平，各年级的科学推理能力水平普遍不高，特别是小学阶段，即使是高中生也有相当一部分学生尚未发展到形式运算思维阶段。传统教学习惯性沿用固有材料引导学生，同一教学思路应对众多不同的学生个体，缺乏兼顾学生已有认知的本位思考；因此学生也习惯性沿着单一路径考虑问题。学生在分析和解决问题时，不能从多角度多途径地思考，思维惯性难以发散或多维变换角度，缺乏思维的综合训练和优化，无法提高科学思维素养。我国教育工作者需要重新审视教学行为是否吻合最新课程标准对培养科学思维能力的提倡和要求。教师努力启发学生思维的灵活性与发散性，能够从多角度、全方位思考问题，冲破传统观固定化思维模式的单一性与局限性，为学生播下创新思维的种子。

(三)重视培养估算能力的教学

如何科学有效地培养学生的计算能力一直是国际教育研究的重要话题。计算能力包括精确计算和估算能力，二者在大脑上分属不同的脑区，共同组成个体计算能力。精算能力培养是数学教育长期培养的重点，而估算能力同样受到国内外教育界的高度重视。1980年和1990年，美国数学教师联合会 (NCTM)明确将估算能力培养列入数学教育的重要目标。英国、荷兰、法国等国家也纷纷将估算能力纳入正式课程，我国《全日制义务教育数学课程标准(实验稿)》中也将估算作为数感的重要内容。精算能力是一种程序化和精确化的认知能力，其认知过程表现出较强的时间线性特点。估算能力的认知则表现出较强的直觉性和内隐化特点。[37]我国学生在精算能力上的表现优于美国学生，而在概率等估算能力上落后于美国学生。可见，我国对计算能力的培养侧重于精算，而忽视了估算能力。精算能力和估算能力在个体计算能力发展上同等重要，在教学过程中均应当受到重视。如果教学只注重精算能力的培养，追求计算的精确性和严谨性，那么估算技能缺乏足够的训练，学生对数感的直觉性感知会不足，缺乏数学思维的直觉能力和变通能力。同时，精算和估算不是完全独立，二者是紧密相连的：功能核磁共振图像研究表明脑区的激活是相互促进的[38]，如与估算相关的脑区被激活时，临近的与精算相关的脑区也会被激活。同时，精算能力和估算能力具有互补性：精算能力能有效提高解决问题的精确性，但耗时长，估算能力能帮助快速搜索问题答案，但准确性不足。在大力提倡素质教育的今天，我们应重视估算教学，培养学生的估算意识，发展学生的估算能力，让学生拥有良好的估算素养。