二叉树模型在目标跟踪中的应用
2020-02-12郑运平李睿君
郑运平 李睿君
(华南理工大学 计算机科学与工程学院,广东 广州 510006)
自从目标跟踪的需求出现以来,尤其是近十年来,目标跟踪算法层出不穷,不同跟踪算法建立的模型、选取的特征也不相同。目标跟踪算法根据模型可大体分为两类:生成式[1- 5]和判别式[6- 19]。其中生成式先构造一个模型描述目标的外观信息、结构特征,往往是像素值、梯度等直观信息,再去候选区域中寻找与模型最匹配的区域。判别式的思路是训练一个分类器,不仅在目标区域内采取正样本,同时在目标周围的背景区域采取负样本,利用到前景和背景的差异信息,用该分类器去评估候选区域与目标区域的接近程度。
比较经典的生成式模型有:高斯混合模型(Gaussians Mixture Model,GMM)、贝叶斯模型(Bayesian Network Model,BNM)、马尔可夫随机场模型(Markov Random Field,MFR)[1]。早在1999年,Marques等[2]就结合高斯混合模型和隐马尔科夫模型提出了一种跟踪具有复杂形状的目标的算法。2016年,Miao等[3]为目标确定基于SURF(Speeded Up Robust Features)的关键点,为每个关键点构建动态的缩放-旋转空间,以加强其变化和独特性,并用高斯混合模型为每个关键点分配一个内核权重,以确保使用更加可靠的关键点,提高了跟踪算法在复杂场景变化下的鲁棒性。2018年,Zhu等[4]基于Vibe和高斯混合模型,使用视频序列训练“虚拟”背景模型而不是用第一帧图像建模,然后基于像素分类提取前景像素,比主流的背景减法更能适应复杂场景,且速度更快;同年,Ahmad等[5]提出一种概率推理方法,根据实际应用情况和贝叶斯网络预测目标的意图预测它的目的地和轨迹,充分利用了轨迹中潜在的长期依赖性,在实际应用中很有价值。
比较著名的判别式算法有:Struck、TLD(Tracking-Learning-Detection)、CT(Compressive Tracking)和基于CF改进的KCF(Kernelized Correlation Filter)[6- 19]。2011年,Hare等[6- 7]提出的Struck算法风靡一时,与当时其他算法相比不仅跟踪效果好,还能达到实时要求;该算法提出一种基于结构输出预测的自适应视觉目标跟踪框架,通过明确引入输出空间满足跟踪功能,能够避免中间分类环节,直接输出跟踪结果; 同时,为了保证实时性,该算法还引入了阈值机制,防止跟踪过程中支持向量的过增长。TLD算法[8- 9]是一种主要针对单目标长时间的跟踪算法,分为检测、追踪、学习3个模块; 该算法与传统跟踪算法的显著区别在于将跟踪算法和检测算法相结合,来应对目标发生较大形变或长时间遮挡等情况;后来也有许多研究者对其进行改进,或者应用它的思想优化其他跟踪算法[10- 12]。CT算法[13]利用了压缩感知的理论,先获取图像的高维特征,再用稀疏随机测量矩阵对特征进行降维,从而大幅减少运算量,这令CT算法以跟踪速度快而闻名。2011年,Babenko等[14]引入MIL(Multipe Instance Learning)方法取代传统的有监督学习,以便产生鲁棒性更强且参数设定更少的追踪器。KCF[15- 18]是基于相关滤波的代表性算法之一,借助循环矩阵和傅里叶变换,将矩阵运算转换为向量的点积,实现极高的跟踪速度,同时保有不错的跟踪准确性;与之相似的还有DCF(Discriminative Correlation Filter)[19],两者都是基于CSK改进的,只是核函数不同——KCF采用高斯核函数,而DCF采用线性核函数。
就当前比较先进的算法而言,生成式算法的表现整体不如判别式算法,但是目标跟踪的场景多种多样,不同场景的目标运动特征不同,由于生成式算法比判别式算法带有更丰富的图像信息,对于快速移动、环境复杂的情景往往更具优势。此外,部分判别式算法用到了深度学习来训练分类器,这要求较大的训练数据量,而大部分时候目标跟踪问题只会在视频的第一帧给出目标区域,这个数据量是不够的。因此,具体到某些实际应用问题,生成式算法也有自己的优势。
生成式算法表现欠佳,主要的一个原因是跟踪速度慢,因为生成式模型需要的计算量较大。针对这个问题,有一类模型可以进行优化,即分块模型。由于图像的冗余性,可以用分块整体代替多个像素来描述局部特征,同时减少运算量,各块的特征则共同描述了该目标的内部特征。值得注意的是这类模型与很多经典的生成式模型并不冲突,比如高斯混合模型是对每个像素建模,这种方法将点组合成块,以块为单位对整个子空间进行操作,显然能大幅减少运算时间。对于这种模型,分块数目与目标跟踪速度直接相关,分块越多,跟踪速度越慢。
2015年张文俊等[20]提出了一种基于四叉树分块的模型,基本思路是将图像等分为4部分,对每一个子块进行判断,若该子块各像素的灰度值相似程度达到某个阈值,则计算该子块的特征,反之将该子块进一步等分为4部分,重复上述过程。他们在实验中将同一分块的像素近似为高斯分布,并用两个分布之间的KL距离来衡量两个相同规模分块的相似程度。其实验结果表明,该模型应用于目标跟踪,在准确率上普遍优于CT算法、MIL算法,但是在耗时上还是处于劣势。
有效的图像表示方法不仅能节省图像的存储空间,而且还能提高图像处理的速度[21- 23]。考虑到耗时与分块数直接相关,上述跟踪算法的效率很大程度上受限于四叉树模型产生的分块数,本研究将采用分块数大幅减少的二叉树模型作为目标特征的描述模型;同时,在分块时采用自己关于同类块的定义,从而使得后面计算每个分块的特征时能用分块均值来近似表示,避免计算高斯分布参数时繁杂的平方计算;另外,在跟踪时依据下一帧选取的目标区域与当前帧的目标区域之间的差值来判断是否需要重新划分,更好地适应目标发生变化的情况。
1 图像的二叉树分块模型
1.1 二叉树分块方法
基本的二叉树分块方法主要步骤有:
步骤1将当前图像记为当前块,压入容器中。
步骤2从头开始遍历容器,对遍历到的当前块作判断,直至容器结尾——若当前块符合终止划分条件则不做处理,继续遍历容器中的下一个块; 反之,对当前块进行二等分,将分割得到的两个子块压入该容器中,并将其父块(即当前块)从容器中去除。
在以上步骤中,需要考虑两个问题:一是判定是否终止划分的标准; 二是需要采用何种数据结构和哪些特征信息来描述每个分块和整幅图像。
1.2 同类块判定标准
本研究采用判断当前块是否符合同类块的定义来作为终止划分的标准[24]。同类块的定义见定义1。
定义1给定一个误差容许量ε,若一个矩形块B内所有像素值g(x,y)均满足|g(x,y)-gest(x,y)|≤ε,则称该矩形块为同类块(如图1所示),其中,x1≤x≤x2、y1≤y≤y2,gest(x,y)是B中坐标(x,y)处的近似灰度值,其计算公式为
gest(x,y)=g5+(g6-g5)×i1
(1)
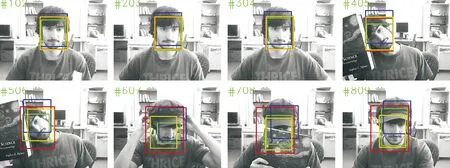
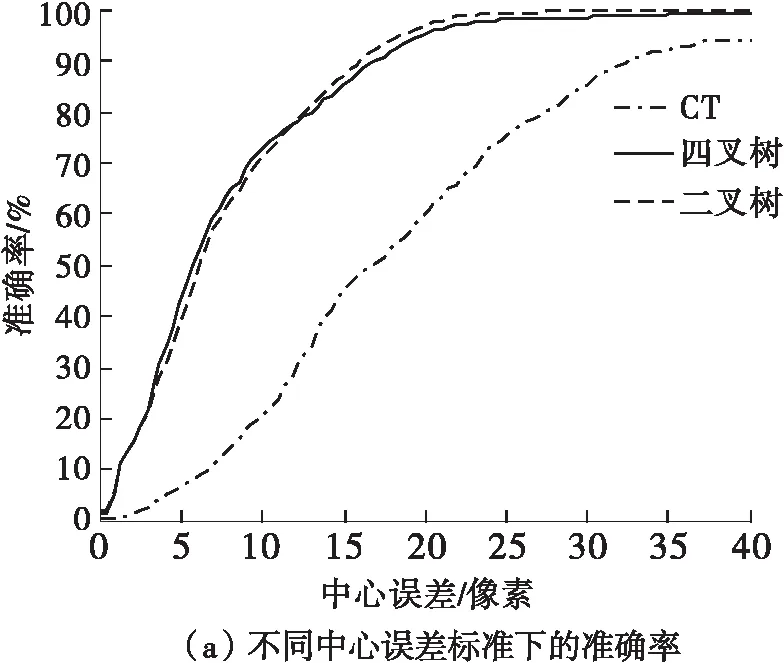
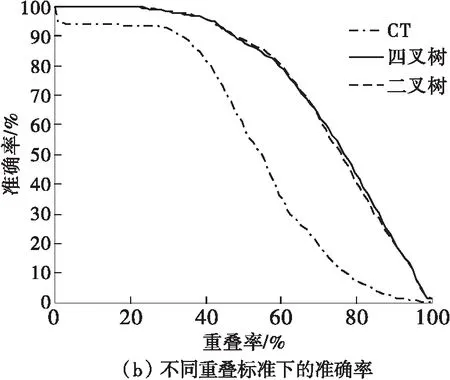
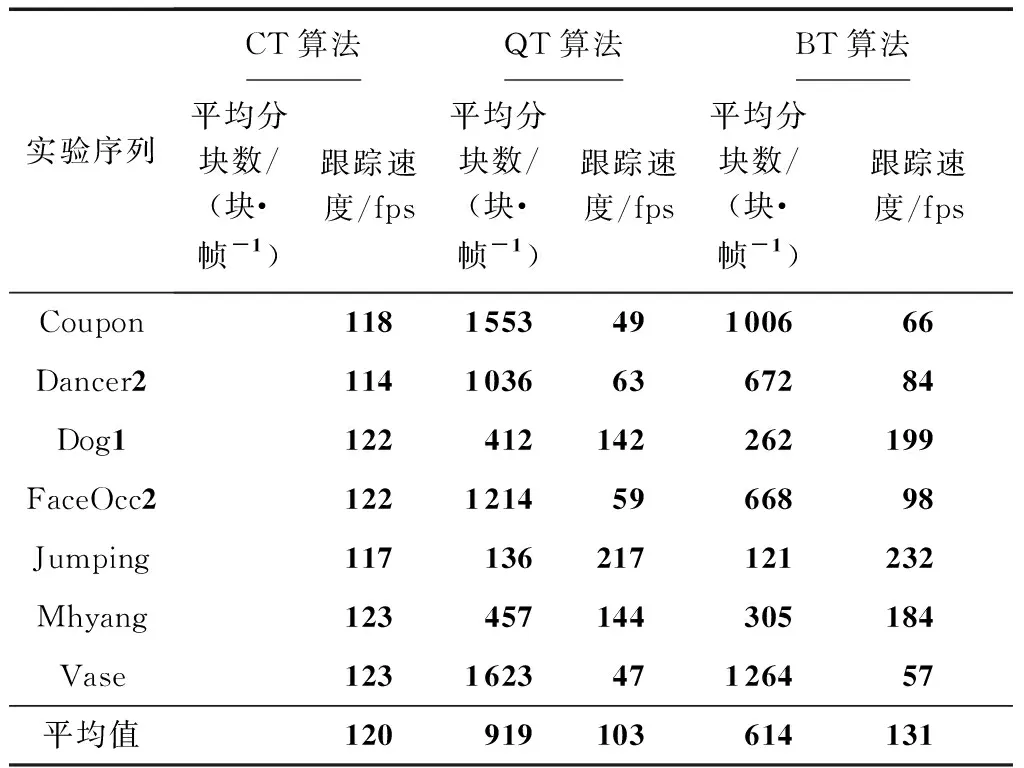
其中,g1、g2、g3和g4是该块4个角落的灰度值,g5=g1+(g2-g1)×i2,g6=g3+(g4-g3)×i2,i1=(y-y1)/(y2-y1),i2=(x-x1)/(x2-x1),x1 若当前块是一个同类块,则终止划分;否则继续划分。 图1 同类块B的示意图 对于每个同类块,需要记录的信息包括位置信息和特征信息。 对于位置信息,直接记录同类块的左上角顶点位置和长宽信息。 对于特征信息,参考了张文俊等[20]的实验。文献[20]中指出,四叉树分块的结果会使每个分块的像素分布呈高斯分布,因此他们记录了每个分块的均值和方差。对于二叉树分块来说这也同样适用,但是笔者在实验中发现了两个问题:一是计算方差的效率非常低,很难达到实时跟踪的效果; 二是在寻找接近目标区域的候选框时,同一分块内的像素并不适合用高斯分布来近似,这是因为对候选区域采用的划分方法需要与目标区域的划分方法保持一致,但这不能保证候选区域分割得到的分块同样满足同类块定义,即同一分块的像素并不满足高斯分布,此时继续用高斯分布来近似和计算候选区域与目标区域之间的KL距离,意义不大,尤其是分块较小时,由于像素个数太少,比较容易出现方差为0的情况,此时KL距离会趋于无穷大,不易处理。因此本研究采用了更简化的评估方式,仅记录每个分块的大小和均值。首先它在运算时间上是能达到实时跟踪的; 其次,实验表明这种特征描述方式是有效的。 为了适应在跟踪过程中目标区域发生大小变化,本研究记录同类块位置信息和大小时均采用其相对于目标区域的百分比来记录。 综上,本研究采用的特征描述向量为 (average,percent,x,y,width,height), 即:(灰度均值,面积权重,左上角顶点横坐标,左上角顶点纵坐标,宽度,高度)。 后面5个值均是[0,1]之间的百分数。 本研究采用的二叉树分块算法如下。 /*给定一幅M×N的灰度图像和误差(阈值)ε,指定目标区域B,输出一个描述B特征的同类块特征模型(特征表)F*/ 步骤1初始化一个元素类型为矩形的队列V,将目标区域B对应的矩形压入V中。 步骤2判断V是否为空,若V为空,算法结束; 否则转入步骤3。 步骤3取出队列V头部的矩形,根据式(1)判断其是否为同类块。如果它是同类块,计算它的特征描述向量,将特征向量压入特征表F中;若它不是同类块,将其二等分,将得到的两个矩形依次压入队列V尾部。 步骤4返回步骤2。 每1次四叉树划分,都可以把它分解为3次二叉树划分的叠加。对于1个父块,先二分为2个中间块,每个中间块再分别进行1次二分,最终得到4个子块,该结果与1次四叉树划分是完全相同的。因此如果一个二叉树未提前终止,持续划分下去,最终必定会达到与四叉树划分相同的结果(相同阈值下)。在划分过程中,分块数显然是递增的,因此二叉树的分块数目不可能超过四叉树分块数目。而由于二叉树会对中间块进行判断,如果中间块达到同类块的要求,则终止划分,此时二叉树的分块数目就会比四叉树少。在本研究后续的实验中统计了相同阈值下二叉树和四叉树的分块结果,证明了二叉树分块数明显少于四叉树分块数。 假定所要跟踪的目标在第一帧中人为给出,通过第1节的算法可得到由目标区域分块而来的特征表F,此后,在每一帧中,寻找最接近目标特征的区域。假设有m个矩形候选区域,对每一个候选区域进行分块,分块方式与目标区域的分块方式相同,按F的分块顺序计算候选区域每个分块的特征,可得到与F相同大小的候选框特征表Fi,假设分块块数为n,第i(1≤x≤m)个候选区域与目标区域之间的特征差值计算方法如下: di=∑(disi,j×F(j)percent) (2) disi,j=Fi(j)average-F(j)average (3) 其中:disi,j表示第i个候选区域第j个分块与目标区域第j个分块之间的差距,文中用像素均值的差值来表示;F(j)average表示F(j)的均值分量(F(j)表示目标区域第j个分块对应的特征,即特征表F的第j个元素);F(j)percent和F(j)average依此类推。 考虑目标跟踪的特性,本研究总是从当前目标区域附近选取候选框,比较各候选框的特征,从中选取最接近目标特征的一个作为结果。选定结果后,需根据该结果更新目标区域的特征表。更新特征表有两种情况,如果下一帧选取的目标区域与当前帧的目标区域差别过大,超出设定的阈值,则认为目标区域很可能发生较大改变,将重新进行二叉树划分; 反之,如果两者差别不大,未超过阈值,将参考在原来的划分基础上对特征表的均值进行更新。具体算法如下。 /*给定一系列连续帧,给出初始目标区域B的位置,在每帧中找出目标区域并框选出来*/ 步骤1应用第1节的二叉树分块算法对目标区域B进行划分,得到描述目标信息的特征表F。 步骤2设定候选框搜索半径r,以当前目标区域位置为中心、r为半径、3为步长在下一帧搜索候选区域,并计算每个候选区域的特征表; 按式(2)和式(3)计算每一个候选框与当前目标区域B间的特征差值di,将di最小的候选框记为temptRect。 步骤3以temptRect为中心、1为半径、1为步长在下一帧搜索候选区域,并计算每个候选区域的特征表; 按式(2)和式(3)计算每一个候选框与当前目标区域B间的特征差值di,将temptRect重新赋值为di最小的候选框。 步骤4判断temptRect与当前帧目标区域的特征差值di是否大于阈值threshold,如果是,则进入步骤5; 否则进入步骤7。 步骤5设定放大及缩小参数increase和decrease,以temptRect为中心,分别放大increase、increase×increase倍和缩小至decrease、decrease×decrease得到矩形候选区域,并计算每个候选区域的特征表。计算每一个候选框与当前目标区域间的特征差值di,将temptRect重新赋值为di最小的候选框。 步骤6将temptRect作为下一帧的目标区域,判断temptRect与当前帧目标区域的特征差值di是否大于阈值threshold,如果是,重新对temptRect进行二叉树划分得到新的特征表F,否则不需要进行二叉树划分,直接通过下式更新特征表F: F(j)average=temptRect(j)average×λ+ F(j)average×(1-λ) (4) 其中:F(j)average、tempRect(j)average分别表示F(j) 的均值分量、temptRect第j个分块的均值分量;λ为变化速度参数,计算方法为 λ=rate/(1+di) (5) 其中rate是设定的更新参数。 步骤7如果没有后续帧,则算法终止,否则返回步骤2。 文中从准确性和跟踪速度两个方面对CT算法、基于四叉树模型的算法(简称QT算法)和本研究提出的基于二叉树模型的算法(简称BT算法)进行了比较。CT算法代码来自张开华等[13]提供的开源代码:http:∥www4.comp.polyu.edu.hk/~cslzhang/CT/CT.htm。QT算法参考了张文俊等[20]的论文。 实验中的测试图像全部来自OTB100[25- 26]。实验操作系统为64位的Windows10系统,处理器为Intel(R)Core(TM)i5-8500,处理器频率为3GHz,运行内存RAM为8GB。 对于QT算法和BT算法,参数设定如下: 同类块判定阈值ε=20; 候选框搜索半径r=25; 特征差值阈值threshold=30; 候选框大小的增幅increase=1.1; 候选框大小的缩幅decrease=0.9; 更新速率rate=0.5; 实验结果如图2、图3及表1所示。图2中蓝色矩形框、红色矩形框、黄色矩形框分别代表CT算法、QT算法和BT算法的结果,绿色矩形框代表正确的目标区域。 (a)Coupon跟踪结果 (b)Dancer 2跟踪结果 (c)Dog 1跟踪结果 (d)FaceOcc 2跟踪结果 (e)Jumping跟踪结果 (f)Mhyang跟踪结果 (g)Vase跟踪结果 就BT算法与QT算法而言,由图2的直接观察和图3的量化统计可知,BT算法的跟踪准确性与QT算法大致相当。但由表1可以算出,与QT算法相比,BT算法的跟踪速度大幅提高,提高了27.18%((131-103)/103×100%)。主要原因是分块数目明显减少,同类块平均分块数减少了33.19%((919-614)/919×100%),由此可见BT算法比起QT算法在跟踪速度上有很大优势。 就BT算法与CT算法而言,图3表明,在跟踪准确性方面,无论是以跟踪区域与目标区域间的中心误差,还是以跟踪区域与目标区域间的重叠率作为评价标准,BT算法都要远远优于CT算法。从图2可以看出,BT算法的跟踪效果要明显优于CT算法。而在跟踪速度方面,表1所示结果表明BT算法的平均水平也高于CT算法。单独分析基于二叉树模型的跟踪算法不难看出,其跟踪速度与分块数直接相关。 综上所述,与基于QT的跟踪算法相比,基于BT的跟踪算法在准确性方面几乎不受影响的前提下,跟踪速度显著提升; 与基于判别式的CT算法相比,在跟踪速度大致相当的前提下,基于BT的跟踪算法跟踪准确性却更好。因此,文中提出的基于BT的跟踪算法是一种更有效的目标跟踪方法。 图3 3种算法跟踪准确率的比较 表13种算法平均分块数和跟踪速度比较 Table1Comparison of average number of blocks and tracking speed of the three algorithms 实验序列CT算法QT算法BT算法平均分块数/(块·帧-1)跟踪速度/fps平均分块数/(块·帧-1)跟踪速度/fps平均分块数/(块·帧-1)跟踪速度/fpsCoupon118155349100666Dancer211410366367284Dog1122412142262199FaceOcc212212145966898Jumping117136217121232Mhyang123457144305184Vase123162347126457平均值120919103614131 通过用二叉树分块模型描述目标区域的特征,文中提出了一种基于二叉树模型的目标跟踪算法。本算法与著名的压缩跟踪算法以及基于四叉树模型的跟踪算法进行比较,理论分析和实验结果证明了本算法在速度和准确性上的优越性。事实上,文中提出的算法还可以进一步优化,比如在候选框的选取、二叉树分块终止条件等方面进行改进,可以减少候选框的个数或目标区域的分块数,从而提高跟踪速度; 或者是修改同类块特征的选取。文中主要是从分块的角度论述二叉树模型在目标跟踪中的应用价值,在描述分块特征时完全可以结合其他特征表示模型来进行改进,比如梯度直方图、高斯混合模型等; 还可以将同类块阈值设置为可动态自适应的,从而适应不同类型视频的要求、稳定跟踪速度等等。因此这一模型还有很大的潜力和改进空间。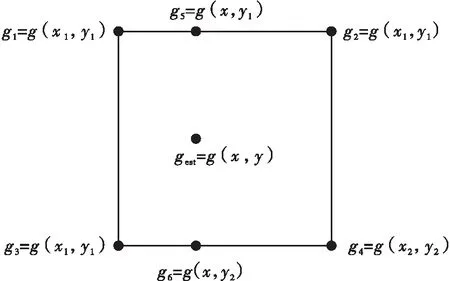
1.3 特征记录
1.4 二叉树与四叉树的比较
2 二叉树模型在目标跟踪中的应用
3 实验结果与分析






4 结语
