组合多粒度粗糙集及其在教学评价中的应用

钟诚，李金海



组合多粒度粗糙集及其在教学评价中的应用

钟诚1，李金海2

(1. 海南热带海洋学院海洋信息工程学院，海南三亚 572022；2. 昆明理工大学理学院昆明 650500）

本文通过分析现有的多粒度粗糙集在确定性决策中的不足，提出一种组合多粒度粗糙集，定义组合多粒度粗糙集的下、上近似集，研究组合多粒度粗糙集的性质，并讨论几种多粒度粗糙集的度量因子之间的关系。最后通过教学质量的决策评价分析，验证了所提出的模型是可行的。

多粒度粗糙集；组合多粒度粗糙集；教学评价

引言

经典粗糙集理论[1-3]是通过单个等价关系对知识库诱导出的知识粒来近似逼近目标概念.钱宇华等[4-6]提出由一族等价关系诱导出的知识粒来近似逼近目标概念。近几年多粒度粗糙集受到众多学者的关注,并对经典多粒度粗糙集进行多种形式上的拓展。例如，优势关系多粒度粗糙集[7-9]、可变多粒度粗糙集[10-12]、程度多粒度粗糙集[13]、邻域系统多粒度粗糙集[14]、基于等价关系的混合多粒度粗糙集[15]、相似关系变精度多粒度粗糙集[16]等。

经典多粒度粗糙集决策理论中，乐观决策，是要求只要有其一粒度所诱导出的知识粒是目标概念的子集即可；悲观决策，是要求所有粒度各自诱导出的知识粒都是目标概念的子集。文献[15]采用混合粒度空间来定义的混合多粒度粗糙集，即在析取粒度空间中求合取或在合取粒度空间中求析取的分析方法。显然,经典多粒度粗糙集和混合多粒度粗糙集的决策形式,都是将各粒度空间对决策的影响视为等同。然而，在很多实际问题中，各粒度空间对决策的影响是不尽相同，如要求某部分粒度是:各自诱导出的知识粒必须与目标概念存在包含关系；另一部分粒度的要求是：各自诱导出的知识粒有其一与目标概念存在包含关系即可。例如，在教学比赛中，评委通常由数名与参赛对象的专业相同的高职称教师和数名教学督导（与参赛对象专业不相同）组成，若要求所有评委的评价意见都是优秀，参赛对象才能最终确定为优秀，这样的决策要求太高；若仅要求任一评委的评价意见是优秀，才为优秀，显然这样的决策又太宽松。为此，本文提出将乐观和悲观多粒度粗糙集扩展到带有背景知识的多粒度粗糙集，即将语义析取与语义合取引入论域划分中得到刻画目标概念的新下、上近似算子。文中将其称为组合多粒度粗糙集，并研究组合多粒度粗糙集的性质，讨论组合多粒度粗糙集与乐观、悲观多粒度粗糙集之间的关系.最后通过实例分析验证。

1 粗糙集的基本知识

定义1[2]设为一个信息系统,那么对于的每个属性子集,都可以得到一个二元不可区分关系：

定义2[6]设为一个信息系统，令是的个属性子集，定义关于属性的乐观多粒度粗糙集的下、上近似分别为：

.

定理1[10]设为一个信息系统，令是的个属性子集,可得：

定义3[4]设为一个信息系统，令是的个属性子集,定义关于属性的悲观多粒度粗糙集的下、上近似分别为：

.

定理2[10]设为一个信息系统，令是的个属性子集,可得：

2 组合多粒度粗糙集

在经典多粒度粗糙集决策理论中，乐观、悲观多粒度决策对待各粒度的态度分别相同。然而，在很多实际问题中，各粒度对目标决策的影响是不尽相同的。本文从粒度对目标决策的影响角度考虑，将粒度分为乐观粒度（属性），即采用乐观决策分析的粒度，和悲观粒度（属性），即采用悲观决策分析的粒度，并将语义析取与语义合取引入论域划分中得到刻画目标概念的新下、上近似算子。也就是本节要讨论的组合多粒度粗糙集。

从定义4可以看出，目标概念的下近似逼近是：通过对乐观属性和悲观属性分别按照经典的乐观、悲观多粒度粗糙集的下近似逼近的并集。

证明：由定义2、3、4，可知

证明：由定义2、3、4及定理3，容易证得。

注2 定理4表明组合多粒度粗糙集的下近似比悲观多粒度粗糙集的下近似要宽松，比乐观多粒度粗糙集的下近似要严格；组合多粒度粗糙集的上近似比乐观多粒度粗糙集的上近似要宽松，比悲观多粒度粗糙集的上近似要严格。

2)-3) 根据定义4易证。

注3定理5的1)式表明目标概念与组合多粒度粗糙集的下、上近似之间的包含关系;2)-3)式表明组合多粒度粗糙集的下近似、上近似具有同一运算律；4)式表明组合多粒度粗糙集的下近似、上近似具有单调性;5)式表明组合多粒度粗糙集的下近似、上近似具有互补运算律。

3 多粒度粗糙集度量

下面将经典多粒度粗糙集的几个度量因子的概念引入到组合多粒度粗糙集中，并分别讨论各种度量因子之间的关系。

.

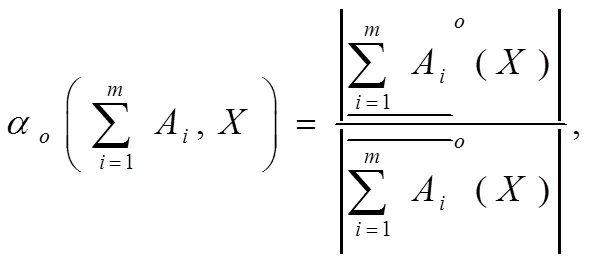
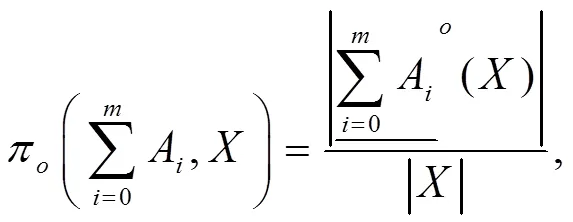
证明1)由定理4，有

注4定理6、7表明: 组合多粒度粗糙集的粗糙精度、近似精度和依赖度因子分别介于乐观和悲观多粒度粗糙集的粗糙精度、近似精度和依赖度因子之间。

4 实例分析

由决策属性得到以下划分：

表1 一个决策信息系统

实际上，经典多粒度粗糙集的决策形式是析取或合取，而本文是将析取与合取进行组合的形式.从以上的计算结果可知，组合多粒度粗糙集的下、上近似集分别介于经典乐观、悲观多粒度粗糙集的下、上近似之间.克服经典多粒度粗糙集要么太宽松，要么太严格的不足。

5 结束语

本文针对经典多粒度粗糙集模型在实际应用中存在的一些不足，建议将乐观和悲观多粒度粗糙集相组合的多粒度粗糙集决策分析方法，通过实例验证了该模型具有一定的实际应用意义。进一步丰富了多粒度粗糙集理论并拓广其应用范围.后续研究包括讨论组合多粒度粗糙集的知识约简，规则提取，等。

[1] Pawlak Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.

[2] Pawlak Z. Rudiments of rough sets [J]. Information Sciences, 2007, 177: 3-27.

[3] Pawlak Z. Rough sets: some extensions [J]. Information Sciences, 2007, 177: 28-40.

[4] Qian Y H, Liang J Y, Wei W. Pessimistic rough decision [C]. The 2nd International Workshop on Rough Sets Theory. Zhoushan, 2010: 440-449.

[5] Qian Y H, Liang J Y, Dang C Y. Incomplete multigranulation rough set [J]. IEEE Transactions on Systems，Man and Cybernetics, 2010, 20: 420-431.

[6] Qian Y H, Liang J Y, Yao Y Y，et al. MGRS: A multigranulation rough set [J]. Information Sciences, 2010, 180(6): 949-970.

[7] 李气芳, 李进金, 林国平.优势关系下的多粒度粗糙集[J]. 计算机工程与应用, 2012, 48(17): 53-57．

[8] 韦碧鹏, 吕跃进, 李金海.基于α优势关系粗糙集模型的属性约简[J].智能系统学报, 2014, 9(2): 251-258.

[9] 徐伟华, 罗术群, 张先韬, 孔莎莎.多源环境下学生综合素质的决策分析[J]. 模糊系统与数学, 2014(1): 178-183

[10] 张明, 唐振民, 徐维艳, 等.可变多粒度粗糙集模型[J]. 模式识别与人工智能, 2012, 25(4): 709-720.

[11] 张明, 程科, 杨习贝, 等基于加权粒度的多粒度粗糙集[J]. 控制与决策, 2015, 30(2): 222-228.

[12] 张明, 唐振民, 徐维艳, 等.可变粒度粗糙集[J]. 计算机科学, 2011, 38(10): 220-222.

[13] 吴志远, 钟培华, 胡建根.程度多粒度粗糙集[J]. 模糊系统与数学, 2014, 28(3): 165-172.

[14] 杨习贝, 杨静宇.邻域系统粗糙集模型[J]. 南京理工大学学报, 2012, 36(2): 291-295.

[15] 杨习贝, 窦慧莉, 杨静宇.基于等价关系的混合多粒度粗糙集[J].计算机科学, 2012, 39(11): 165-169.

[16] 许韦, 吴陈, 杨习贝.基于相似关系的变精度多粒度粗糙集模型[J]. 科学技术与工程, 2013, 13(9): 2517-2522.

Combined Multi-Granulation Rough Set and Its Application to Teaching Evaluation

ZHONG Cheng1, LI Jinhai2

(1. School of Ocean Information Engineering, Hainan Tropical Ocean University, Sanya Hainan 572022, China; 2. Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China)

This paper analyzes the disadvantages of the existing multi-granulation rough sets in certain decision-making, and then puts forward a new combined multi-granulation rough set. The upper and lower approximations are defined for combined multi-granulation rough set as well as its useful properties. Furthermore, the relationship between measure indices of several multi-granulation rough sets is clarified. Finally, decision-making analysis of the teaching quality shows that the proposed model is feasible.

multi-granulation rough set; combined multi-granulation rough set; teaching evaluation

10.19551/j.cnki.issn1672-9129.2017.01.01

TP18

A

1672-9129(2017)01-0001-05

2017-02-01；

2017-02-10。

海南热带海洋学院青年科研基金（QYQN201515）

钟诚（1981-），男，硕士，讲师，主要研究方向为粗糙集、数据处理；李金海（1984-），男，博士，副教授，主要研究方向为粗糙集、概念格、粒计算。