T型挤出模具平衡流道的设计

麻向军

(华南理工大学 聚合物成型加工工程教育部重点实验室∥聚合物新型成型装备国家工程研究中心，广东 广州 510640)

T型挤出模具结构简单、制造成本低，广泛应用于塑料板材、片材和平膜的挤出成型。为保证这类产品厚度的均匀性，要求熔体出口流率沿模具宽度方向均匀一致[1]。T型模具中，熔体沿歧管流动时其压力呈非线性降低，造成熔体出口流率沿模具宽度方向非线性降低，特别是模具宽度较大时，熔体出口流率沿模具宽度方向的差异性更大[2]。实际生产中通常通过加大歧管的截面尺寸、减小阻流区厚度和/或在模具中加装阻流棒并对其进行调节来改善熔体出口流率沿模具宽度方向的均匀性[3]。加大歧管截面尺寸不仅会增加熔体在流道特别是歧管中的停留时间，而且会降低模具的刚度，而减小阻流区的厚度使模具的挤出压力急剧增加，通常会造成产品的成型难度增大，模具的“蛤壳效应”增大[4- 5]；在模具中加装阻流棒不仅使模具结构变得复杂，而且会降低模具的刚度[3]。一些学者采用数值模拟和优化技术相结合，以熔体出口流率均匀性为优化目标，对阻流棒的形状进行了优化，结果表明，当流道设计不良时，即使调节阻流棒也难以使熔体出口流率沿模具宽度方向的均匀性达到理想状态，而且容易造成熔体滞留[6- 8]。Gifford[9]采用数值模拟研究了改善出口流率均匀性的主要参数，结果表明，改变阻流区形状是提高熔体出口流率均匀性的有效措施。目前，受设计理论的限制，已有研究中关于提高T型模具熔体出口流率均匀性的其他措施(如增加柔性模唇[10]等)在实际应用时增加了制造成本，其流道设计大多基于经验并经过多次试模和修模才能完成，增加了模具制造周期和制造成本。为此，本研究通过对熔体在T型模具流道中的流动进行分析，根据流变学理论对流道结构和尺寸进行理论设计，使熔体出口流率沿模具宽度方向达到均匀。

1 流道几何形状的理论推导

1.1 几何模型

典型T型模具的流道结构如图1所示，由入口区、歧管、阻流区、松弛区和成型区组成。由于阻流区、松弛区和成型区的长度和厚度沿模具宽度方向不变，而熔体在歧管中流动时沿流动方向其压力呈非线性下降，故造成熔体出口流率沿模具宽度方向呈非线性下降。

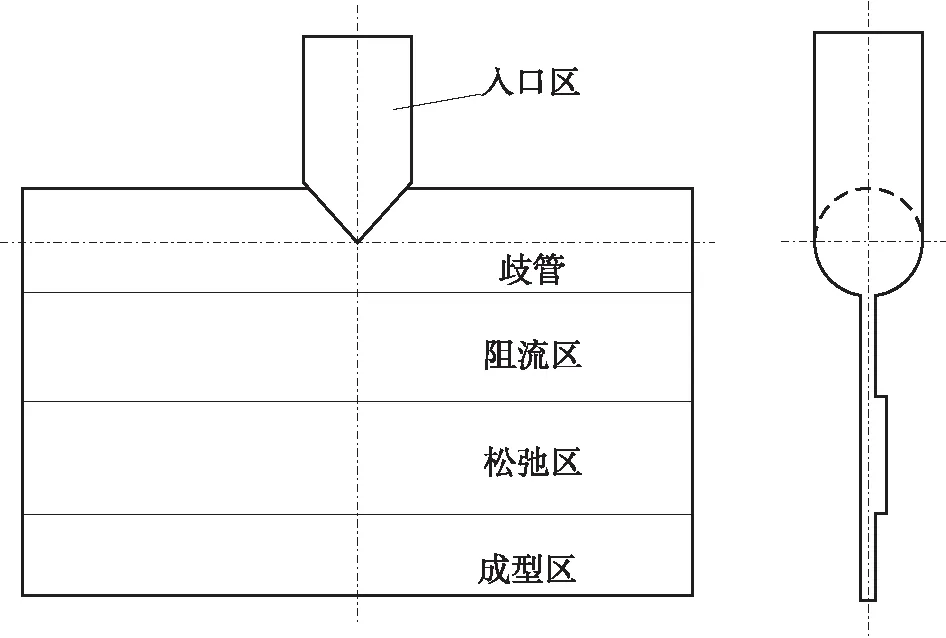
图1 典型T型挤出模具的流道示意图

基于上述分析，在不改变入口区、歧管、松弛区和成型区截面形状的条件下，将阻流区分为厚度不同的两个区域，靠近歧管的区域(阻流I区)厚度较小，靠近松弛区的区域(阻流II区)厚度较大，阻流I区和阻流II区的厚度沿模具宽度方向不变，如图2所示。根据熔体在歧管中的压力沿流动方向的变化特点，保持阻流区总长度沿模具宽度方向不变时，要使熔体出口流率沿模具宽度方向均匀，则阻流I区的长度沿模具宽度两侧方向逐渐减小，而阻流II区的长度沿模具宽度两侧方向逐渐增加。阻流I区在模具末端与歧管之间、阻流II区在流道对称面位置与松弛区之间留有适当间距以方便模具制造。

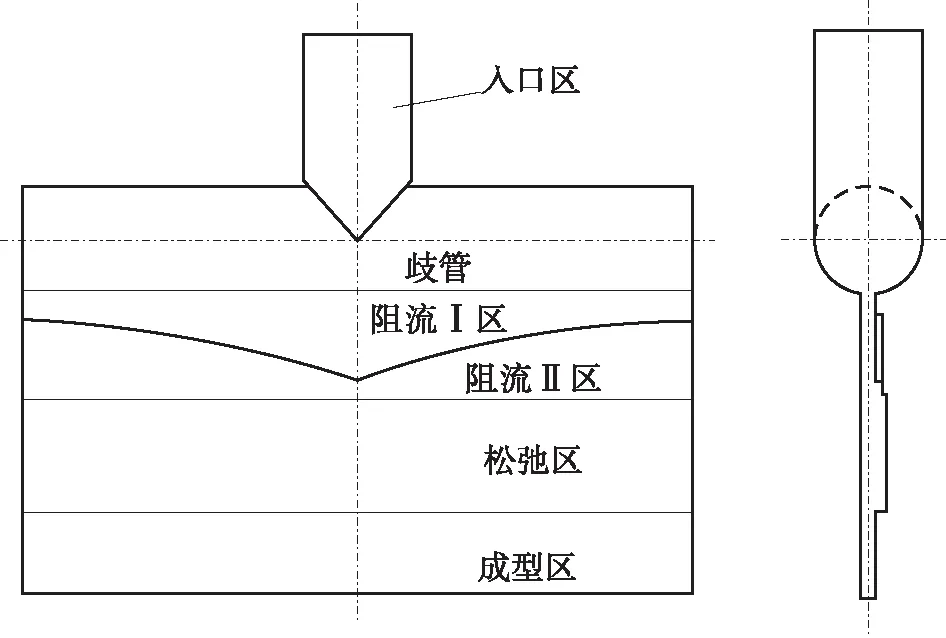
图2 文中提出的T型挤出模具的流道示意图

Fig.2 Diagram of flow channel in T-type extrusion dies proposed in this paper

1.2 物理模型

对于塑料熔体在流道中的流动进行分析时，可做如下假设：

(1)熔体流动为不可压缩流体的稳态层流流动，忽略惯性力和体积力；

(2)熔体在歧管中仅沿歧管轴向流动，在阻流I区、阻流II区、松弛区和成型区中仅沿挤出方向流动，且熔体在歧管中的流动和在阻流I区中的流动互不干涉；

(3)熔体在流动过程中温度不变，其黏度采用幂律模型描述，即

(1)

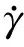
1.3 阻流I区和阻流II区分界形状的理论设计

考虑到流道的对称性，取流道的一半进行分析，如图3所示。为便于分析，忽略入口区的影响，歧管截面选取圆形，其他形状可通过形状因子进行换算。

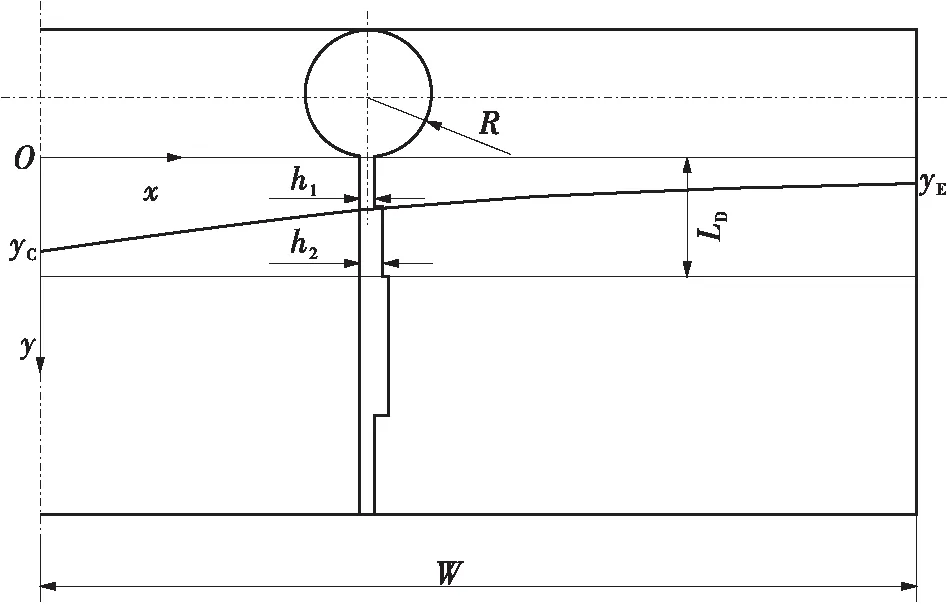
图3 T型挤出模具的流道设计模型

建立如图3所示的坐标系。熔体沿歧管流动时的压力梯度为[11]

(2)

式中：p(x)为歧管中熔体在x处的压力；Q(x)为歧管中熔体在x处的体积流率；R为歧管半径。

假定熔体在模具入口处的体积流率为2Q0。要求熔体出口流率沿模具宽度方向均匀，则歧管中熔体沿模具宽度方向的体积流率为

Q(x)=Q0(1-x/W)

(3)

式中，W为模具宽度的一半。

将式(3)代入式(2)并积分，并假定歧管末端熔体的压力为pE，有

(4)

分析熔体在阻流I区、阻流II区、松弛区和成型区的流动时，可将任一截面x处的流动视为熔体在多个串联狭缝中的流动。设阻流I区和阻流II区的分界形状曲线在模具对称面处的坐标为yC，由于松弛区和成型区的厚度和长度沿模具宽度方向不变，阻流I区和阻流II区的厚度沿模具宽度方向不变，因此，熔体出口流率沿模具宽度方向均匀时，在阻流II区中y=yC处开始，熔体的压力沿模具宽度方向不变。设y=yC时熔体的压力为pC，阻流I区和阻流II区中任一位置x处熔体沿挤出方向流动时，阻流I区入口处(y=0)到y=yC之间的压力降为[8]

(5)

式中：h1和h2分别为阻流I区和阻流II区的厚度，y为阻流I区和阻流II区的分界形状曲线，是坐标x的函数。

在模具宽度方向末端，即x=W时，y=yE，p(x)=pE，代入式(5)得

(6)

由式(4)-(6)可得

(7)

式(7)中的y即为阻流I区和阻流II区的分界形状曲线在图3所示坐标系中的表达式。

1.4 讨论

(1)由式(7)可以看出，阻流I区和阻流II区的分界形状曲线与流道的歧管半径R、宽度W、阻流I区厚度h1和阻流II区厚度h2以及熔体的幂律指数n有关，而与熔体的稠度K和产量Q0无关。

(2)阻流I区在模具宽度方向对称位置(x=0)的长度最大，其长度为

(8)

由式(8)可以看出，阻流I区的最大长度yC随模具宽度W增加而增加，随歧管半径R增加而减小，随阻流I区厚度h1增加而增加，随阻流II区厚度h2增加而减小。模具宽度W由产品规格决定，而歧管半径R、阻流I区厚度h1和阻流II区厚度h2均可作为流道的设计参数，根据熔体的流变特性对阻流I区和阻流II区的分界形状进行设计。

(3) 模具宽度方向对称位置，熔体流经阻流I区和阻流II区的压力降为

pI-pD=

(9)

式中，pI为歧管入口处的熔体压力，pD为阻尼区终止位置的熔体压力，LD为阻尼区的长度。

由式(9)可以看出，可以通过歧管半径R、阻流I区厚度h1和阻流II区厚度h2的设计来调整模具的挤出压力。

(4) 熔体由歧管入口(x=0)到任一位置x所需要的时间t为

(10)

积分式(10)，且x= 0时，t= 0，有

(11)

由式(11)可以看出，熔体在T型模具中流动时，熔体在歧管中的停留时间随流动距离迅速增加，因此，熔体在流道内的流动路径不同，其停留时间不同。

2 阻流区分界形状理论设计的验证

2.1 分界形状曲线理论计算的可靠性验证

为了验证阻流I区和阻流II区的分界形状曲线理论计算的可靠性，采用ANSYS Polyflow软件对熔体在流道中的流动进行数值模拟，通过计算熔体出口流率进行验证。

采用幂律模型描述熔体的流变性能，取幂律指数n=0.5、稠度K=5 000 Pa·s-0.5。取片材的宽度(2W)为1 500 mm、挤出产量(2Q0)为27 000 mm3/s(即挤出速度为10 mm/s)，松弛区的厚度和长度分别取4 mm和45 mm，成型区的厚度和长度分别取1.8 mm和25 mm。阻流I区和阻流II区的总长度取30 mm，取yE=6 mm，对歧管半径R、阻流I区厚度h1、阻流II区厚度h2及阻流I区和阻流II区的分界形状曲线进行设计。

歧管半径分别取15 mm和12 mm。歧管半径R=15 mm时，取h1=1.3 mm、h2=2.5 mm，则y=6+16.2(1-x/750)1.5(单位：mm)，yC=22.2 mm；歧管半径R=12 mm时，取h1=1 mm、h2=2 mm，则y=6+16.3(1-x/750)1.5(单位：mm)，yC=22.3 mm。

考虑到模具宽度方向的对称性，取其一半进行计算。采用8节点六面体单元划分流道，在流道壁面边界、几何突变位置及速度梯度较大的位置采用较小尺寸的网格以提高计算精度，划分后的网格分别约为45万和48万个单元。为进一步提高计算精度，流场计算中速度采用二次插值，压力采用线性插值。

定义熔体出口处沿模具宽度方向某一位置单位宽度的体积流率与宽度方向平均单位宽度的体积流率的比值为单位宽度无量纲流率，用以反映熔体出口流率的均匀性。图4是模拟计算得到的歧管半径为15 mm和12 mm时模具一侧沿模具宽度方向的单位宽度无量纲流率。由图4可以看出，沿模具宽度方向出口流率均匀，仅在流道末端约10 mm的范围内熔体出口流率小于平均流率的99 %，这是因为在理论推导中假定在流道末端熔体与模具侧壁为完全滑移，而在模拟计算时熔体与侧壁之间为无滑移边界，与实际生产一致。

图5是歧管半径为15 mm和12 mm时模拟计算得到的模具一侧流道中熔体的压力场。由图5可以看出，当熔体离开阻尼区时，沿模具宽度方向压力等值线平行于流道出口，从而保证了熔体出口流率沿模具宽度方向的均匀性。歧管半径为15 mm和12 mm时，由模拟计算得到对称面位置熔体流经阻流区的压力降分别为1.73 MPa和2.91 MPa，与理论分析结果一致。

热塑性塑料的热降解量与受热时间成比例增加，因此，熔体在流道中的停留时间是T型模具设计的另一个重要内容[1]。通常，熔体在歧管中的停留时间远大于熔体离开歧管后的停留时间。为便于比较，选择距离歧管入口0.9W处的熔体停留时间进行比较。由式(11)可知，歧管半径为15 mm 和12 mm时，歧管中熔体从入口到达0.9W处时，其停留时间分别为90.4 s和57.9 s。

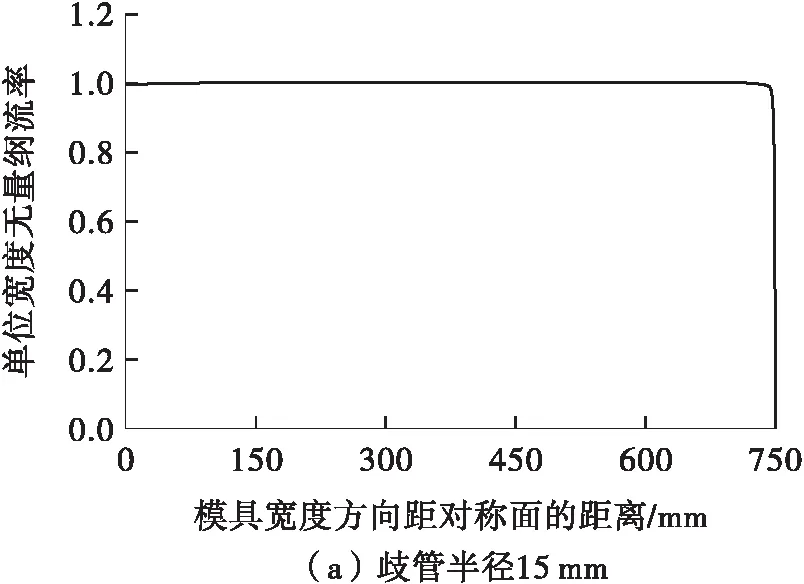
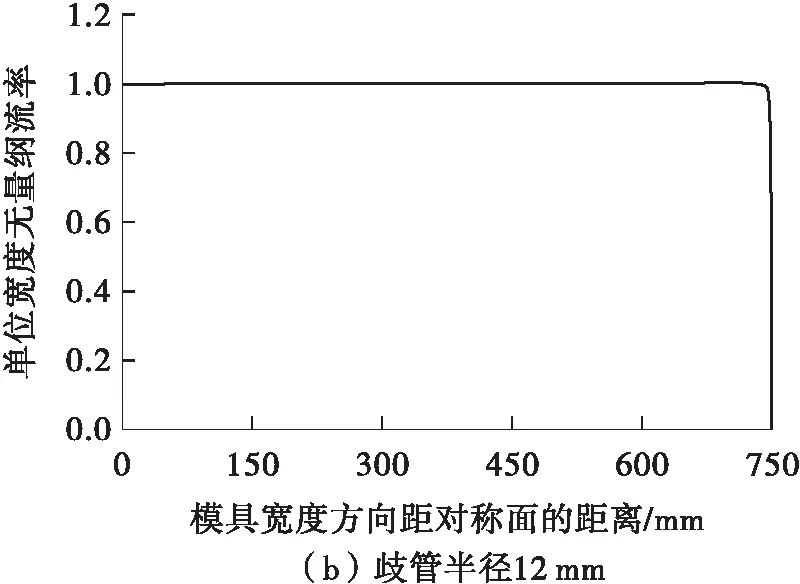
图4 熔体出口流率沿模具宽度方向的变化

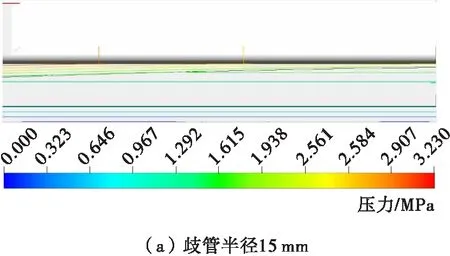
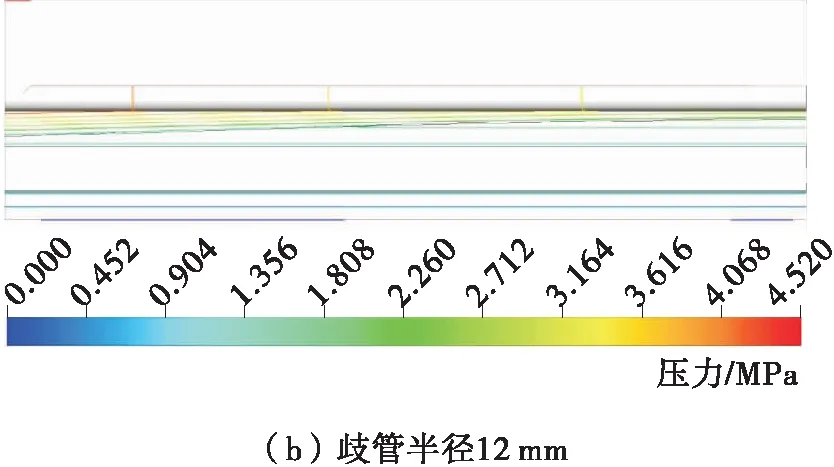
图5 流道中熔体的压力等值线

2.2 与传统设计方法的比较

目前，在T型模具流道设计中，通常以熔体出口流率均匀性指数UI作为流道设计的依据。出口流率均匀性指数定义为熔体在流道末端单位宽度的出口流率与对称面位置单位宽度的出口流率的比值[1]。出口流率均匀性指数与流道几何参数的关系为[1]

(12)

式中，L为阻流区长度，h为阻流区厚度，R为歧管半径，W为模具宽度。传统流道设计中，阻流区的厚度和长度沿模具宽度方向不变。

由式(12)可以看出，增加歧管半径和阻流区长度、减小阻流区厚度，熔体出口流率均匀性提高。就其对熔体出口流率均匀性的影响程度而言，歧管半径的影响最大，阻流区厚度的影响次之，而阻流区长度的影响最小。受模具长度的限制，一般通过增加歧管半径或/和减小阻流区厚度的方法来改善熔体出口流率均匀性。

工程设计中通常要求UI≥0.95。根据式(12)，在松弛区和成型区截面形状和尺寸不变的情况下，如果阻流区采用单一厚度，则歧管半径为15 mm、阻流区厚度为1.3 mm时，UI=0.55；而歧管半径为12 mm、阻流区厚度为1.0 mm时，UI=0.47。可以看出，这两组参数都不能作为设计方案。

为了进一步比较文中提出的设计方法相较于传统设计方法的优越性，针对上述挤出条件且松弛区和成型区几何尺寸不变时，按照传统设计方法对歧管半径和阻流区厚度进行设计。当阻流区厚度分别为1.3 mm和1.0 mm，要使UI≥0.95，则歧管半径R必须大于38 mm和33 mm，对应的模具对称面处熔体在阻流区的压力降分别为2.18 MPa和3.69 MPa，而熔体从歧管入口到达0.9W处的停留时间分别为580.3 s和437.6 s。与文中提出的方法相比，采用单一厚度阻流区时，对称面处熔体在阻流区的压力降分别增加了26.1 %和26.8 %，但熔体停留时间分别增加了5.42倍和6.56倍。熔体出口流率均匀性指数不变时，如果增加阻流区厚度，则必须增加歧管半径，虽然熔体在阻流区的压力降下降，但熔体的停留时间显著增加。

当阻流区厚度减小到0.7 mm时，歧管半径达到26 mm才能满足UI≥0.95，此时，模具对称面处熔体在阻流区的压力降为7.53 MPa，而熔体从歧管入口到达0.9W处的停留时间为271.7 s。与采用文中的设计方法得到的歧管半径为15 mm和12 mm的流道相比，对称面处熔体在阻流区的压力降分别增加了3.35倍和1.59倍，熔体停留时间分别增加了2.01倍和3.69倍。

通过上述比较可以看出，传统的T型模具设计方法在提高熔体出口流率均匀性时，会引起挤出压力显著增加或/和熔体停留时间显著增加，而文中提出的T型模具的设计方法可以在挤出压力和熔体停留时间方面达到较好的均衡。

3 结论

本研究将T型挤出模具的阻流区设计为两个厚度不同的区域，推导了阻流I区和阻流II区的分界形状曲线，利用该设计公式对歧管半径、阻流I区和阻流II区的厚度及其分界形状曲线进行设计，达到了熔体出口流率均匀的目的；然后利用数值模拟对阻流I区和阻流II区的分界形状曲线的理论设计方法进行了验证，结果表明分界形状曲线是可靠的，可用于指导T型挤出模具流道的设计；最后，通过与传统的T型模具设计方法相比较，表明文中提出的设计方法在达到熔体出口流率均匀的条件下，可以有效地减小熔体在歧管中的停留时间和挤出压力。