基于电磁作动的主动吸振器的力特性
2020-02-12傅涛殷智宏任艳上官文斌
傅涛 殷智宏† 任艳 上官文斌
(1.华南理工大学 机械与汽车工程学院,广东 广州 510640;2.宁波润轴汽配有限公司,浙江 宁波 315800)
作为振动控制领域的重要问题之一,动力吸振器已得到了广泛的研究[1- 3]。动力吸振器作为子系统附连在主系统上,通过改变系统振动能量的分布及传递特性,达到抑制主系统振动的目的。传统的动力吸振器属于被动式,其有效减振频带较窄,且由于固有频率不可调节,应用受到限制[4]。为了适应不同的工程背景需求,近年来半主动、主动吸振器发展迅速。半主动吸振器通过调节自身的结构参数,使其固有频率能够跟踪主系统受到的激励力频率,这在一定程度上解决了被动式吸振器有效频带窄的问题;但半主动吸振器的减振效果受其自身阻尼参数的影响较大[5- 6]。主动吸振器是在被动吸振器的基础上增加了作动器,通过接收主系统振动状态的反馈信号,并按一定的控制律实时调节吸振器对主系统施加的驱动力,以抵消主系统受到的激励力,从而达到降低主系统振动的目的;相比被动及半主动吸振器,主动吸振器在宽频内具有更好的减振效果[7]。
国内外学者对主动吸振技术的研究主要集中在作动器的开发和控制算法的研究,而开发出具有良好力特性的作动器是实现主动振动控制的前提。目前,国内外采用的作动器类型主要有压电陶瓷式和电动式。压电陶瓷式作动器所需的驱动电压高、作动力较小,一般较适用于薄板的振动控制[8]。Miroslav等[9-10]、周炜等[11]将压电陶瓷作动器应用于主动吸振器中,并开展了相关的研究工作;Miroslav等[9-10]基于压电陶瓷作动器进行了主动吸振器的开发,并针对柔性梁在单频正弦周期激励和脉冲激励下的振动响应进行了主动控制研究;周炜等[11]对轿车车身板件在发动机激励下的振动进行了主动控制研究,取得了较好的减振效果。电动式作动器采用永磁体提供稳定磁场,使其能够产生较大的作动力,且作动力与电流幅值呈近似线性关系,由于良好的力特性使其在主动吸振器中得到了较多应用[12- 14]。Bohn等[15]采用电动式作动器,对主动吸振器的设计进行了研究,并对由发动机传递到底盘的振动进行了主动控制,车内噪声得到了较大程度的衰减;张洪田等[16]基于船用柴油机的振动特点,利用电动式主动吸振器进行了模拟柴油机台架减振试验;杨恺等[17]为解决航天器轻质柔性结构的宽频振动控制问题,对电动式主动吸振器进行了设计研究。但考虑到永磁体价格昂贵且其性能易受环境温度变化的影响,这较大程度上限制了电动式主动吸振器在实际工程上的应用。
本研究提出了一种基于电磁作动的新型主动吸振器,其作动器采用电磁铁结构。基于对作动器电磁力数学模型进行的理论推导和有限元仿真验证,建立了该主动吸振器的运动学方程,并对其电磁力、驱动力特性进行了研究。考虑到主动吸振器在实际工作中产生的驱动力与理想驱动力之间不可避免的存在偏差,因此理论分析了驱动力在不同的幅值差、相位差以及频率差下主动吸振器的减振效果,并通过搭建简支平板减振试验台,对理论分析结果进行了试验验证。
1 主动吸振器结构
主动吸振技术原理是通过外界供电,使主动吸振器产生具有一定幅值、频率和相位的驱动力,并施加给主系统,与主系统所受的激励力进行抵消,从而抑制主系统的振动。不失一般性,将主系统看作单自由度集中参数系统,主动吸振器简化为单自由度子系统附连在主系统上,两者构成二自由度系统,如图1所示。
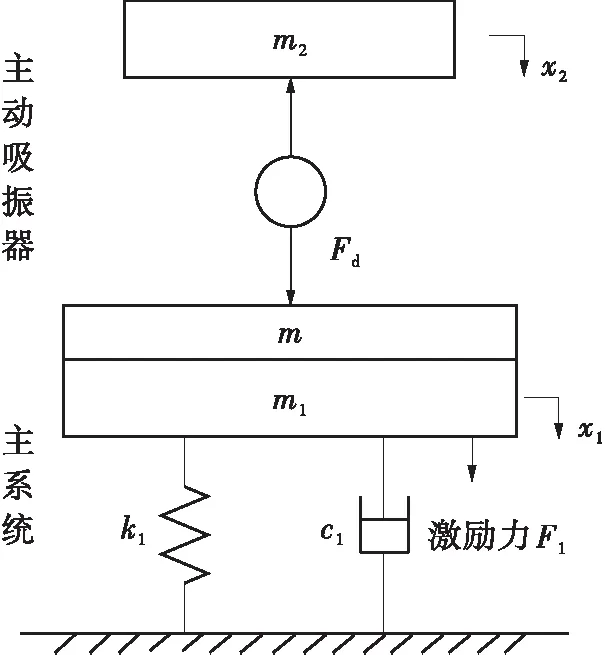
图1 主动吸振系统示意图
忽略主动吸振器的基座质量m,则主系统的运动微分方程为
(1)
式中:m1、k1、c1和x1分别为主系统的动质量、刚度、阻尼和位移;F1为主系统受到的激励力;Fd为主动吸振器对主系统施加的驱动力。
由式(1)可知,当主系统的系统特性(m1、k1、c1)和激励力F1一定时,主系统的振动响应取决于主动吸振器的驱动力Fd,F1+Fd=0时主动吸振器可完全抑制主系统的振动。
文中采用电磁铁为作动器设计了主动吸振器,结构如图2所示。动铁心和线圈构成主动吸振器的动质量m2,静铁心构成主动吸振器的基座质量m,橡胶弹簧提供刚度k2和阻尼c2。动质量通过橡胶弹簧与基座质量相连,当线圈通入交变电流i,动、静铁心之间将产生交变电磁力Fm,在交变电磁力的作用下动质量将产生位移x2。
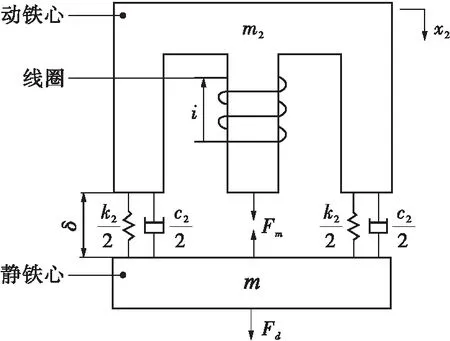
图2主动吸振器结构简图
Fig.2 Structural diagram of the active vibration absorber
根据主动吸振器动质量的运动方程:
(2)
则主动吸振器对主系统施加的驱动力Fd为
(3)
可知在交变电磁力的作用下,主动吸振器的动质量进行往复运动,并对主系统施加与动质量受力方向相反的驱动力。通过控制交变电磁力的幅值、频率和相位即可对主动吸振器的驱动力进行调节。
2 电磁作动器的建模与分析
基于电磁作动原理设计的主动吸振器,当作动器通入交变电流时产生电磁力,并驱动吸振器动质量进行往复运动。因此,为了掌握该主动吸振器的驱动力特性,有必要分析作动器的电磁力特性。
2.1 电磁力数学模型
采用电磁铁结构设计的作动器,主要由动铁心、线圈及静铁心构成。在通电条件下,由于线圈的励磁作用,电磁铁内部产生磁场,其磁路如图3中的虚线所示。
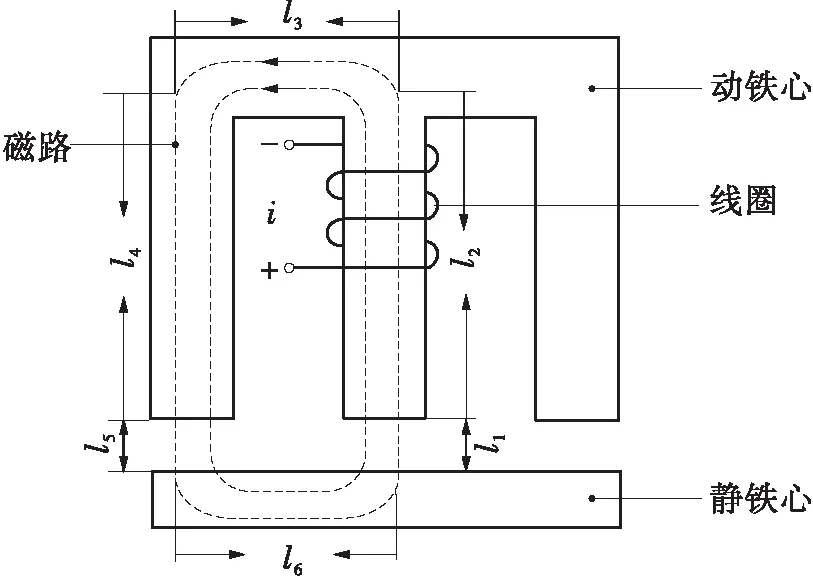
图3 电磁铁结构及磁路示意图
根据基尔霍夫定律和磁通量守恒定律,对电磁铁的磁路进行分析,有:
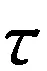
(4)
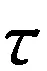
(5)
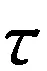
(6)
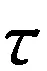
理想条件下,忽略漏磁、铁心的磁阻,并假设气隙中磁场均匀分布且垂直于衔铁表面,则闭合磁路的磁通量为
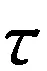
(7)
气隙l1和l5中存在磁场是导致动、静铁心之间产生电磁力的原因,因此为了计算电磁力,首先需要得到气隙磁场强度的计算模型。由式(4)-(7)可得气隙l5的磁场强度H5和气隙l1的磁场强度H1:

(8)

(9)
式(8)中:μ1、μ5为空气相对磁导率(令μa=μ1=μ5);μ2、μ3、μ4和μ6为铁心相对磁导率,动、静铁心采用相同的导磁性材料(令μm=μ2=μ3=μ4=μ6)。由于空气相对磁导率远小于铁心的相对磁导率,即μa≪μm,故将式(8)简化得:

(10)
根据一般化的电磁铁结构,普遍采用的电磁力计算式[18]为
(11)
结合文中设计的电磁铁结构参数,令δ=l1=l5、S1=S5,由式(9)-(11)可得电磁力为
(12)
由式(12)可知,当电磁铁结构、材料一定时,电磁力取决于电流i和气隙δ两个物理量,且与它们有较复杂的非线性关系。
2.2 电磁力有限元仿真
为了验证上述推导的电磁力数学模型的正确性,文中利用电磁场有限元软件Ansoft Maxwell 14.0对电磁铁的电磁力进行仿真计算。对电磁铁作电磁场分析,通过建立有限元模型,确定电磁铁产生的电磁场分布情况,并对电磁铁在不同气隙下的电磁力变化情况进行研究。
2.2.1 分析模型和参数
在有限元电磁场软件Ansoft Maxwell 14.0的静磁场仿真环境中,建立电磁铁三维实体模型,如图4所示。考虑空气的漏磁,建立空气单元将整个实体模型封闭起来,目的是使电磁铁外表面与空气相接处的部分自动定义为边界条件,建立包围整个实体模型区域的求解域。
在有限元模型中,动、静铁心材料选用软件材料库中的Steel- 1008,励磁线圈的材料为铜,导向组件为非导磁性材料,Steel- 1008材料非线性的B-H特性曲线如图5所示。进行电磁力分析时,输入参数为激励电流,在励磁线圈的剖面上施加传导电流;输出参数为动、静铁心受到的电磁力。软件采用四面体结构对各部分进行自适应网格划分,在几何结构突变处增加网格密度,其他地方较稀疏,四面体单元的最大边长值设为5 mm。仿真计算中,对励磁线圈的剖面上施加传导电流,电流幅值I=5 A。
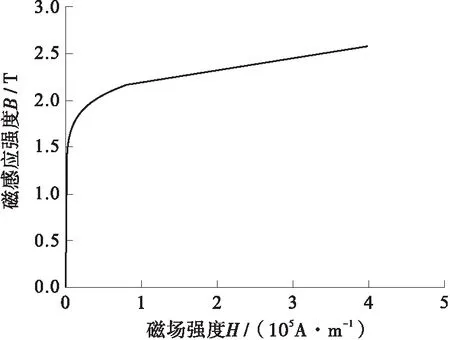
图5 铁心材料B-H 特性曲线
2.2.2 磁场分析
电磁铁磁感应强度分布如图6所示,受线圈励磁作用的影响及导磁材料的约束,磁场在电磁铁内部形成一个由“动铁心-气隙-静铁心”组成的闭合磁路。当线圈通电产生励磁作用时,磁力线以垂直于动铁心下表面的方式穿过气隙进入静铁心上表面。在动铁心中,由于受到动铁心结构形状的约束,磁力线呈倒U形路径进入气隙,使磁力线形成闭合回路。
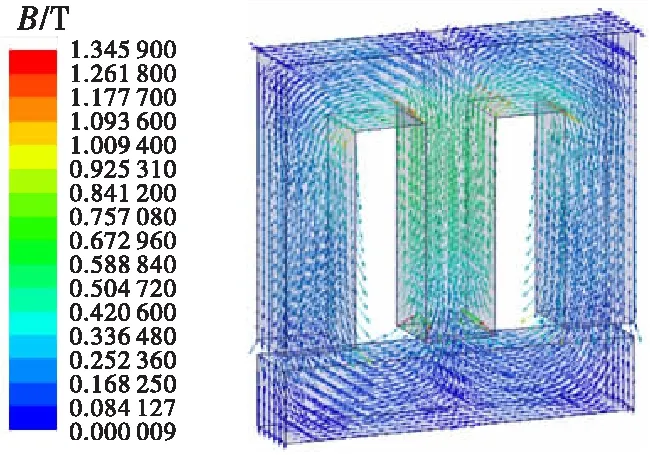
图6 磁感应强度矢量图(δ=4mm)
Fig.6 Vectogram of the magnetic induction intensity(δ=4 mm)
电磁铁气隙中的磁感应强度决定了电磁力的大小,磁感应强度分布云图如图7所示。由图7可见,整个电磁铁内部的磁感应强度关于电磁铁长轴呈对称分布,且电磁感应强度分布较为均匀。通过对电磁铁在不同气隙下的磁场进行仿真,研究气隙磁感应强度分布,由于气隙中磁场均匀分布,故获取气隙中线(图7中A、B为中线端点)上的磁感应强度来分析不同气隙下的磁场变化特性,结果如图8所示。
由图8可知,气隙对磁感应强度的影响较大,气隙越小磁感应强度越大。相比两侧的气隙磁感应强度,中间气隙磁感应强度更大且接近两倍的关系,这与式(9)的结论一致。对电磁铁的电磁力进行仿真计算,并与理论模型(式(12))的计算结果进行对比,如图9所示。由图9可见,理论计算结果与有限元计算结果在趋势上一致,均符合随着气隙减小,电磁力非线性增大的趋势。
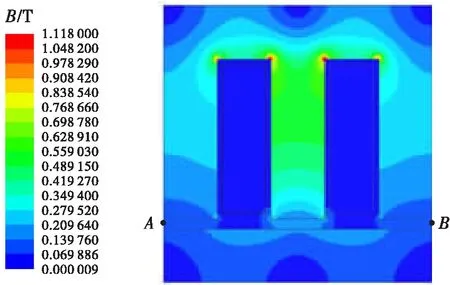
图7 磁感应强度分布云图(δ=4 mm)
Fig.7 Nephogram of the magnetic induction intensity(δ=4 mm)
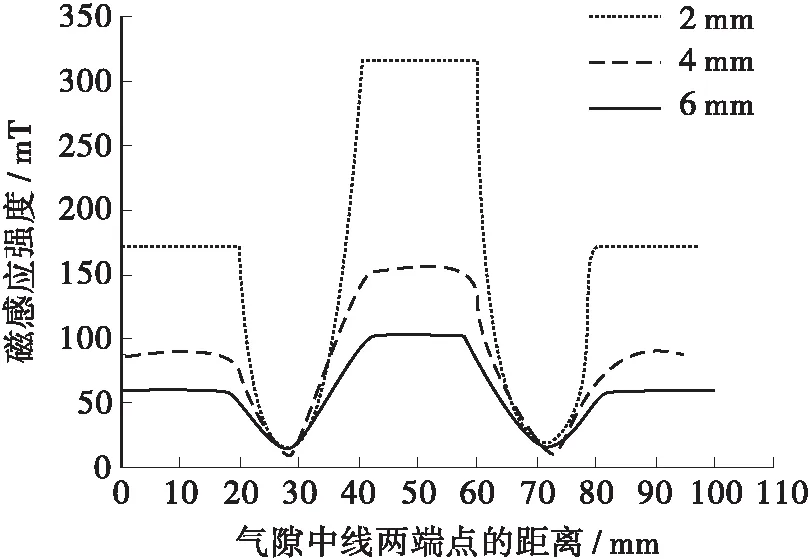
图8 不同气隙下的磁感应强度
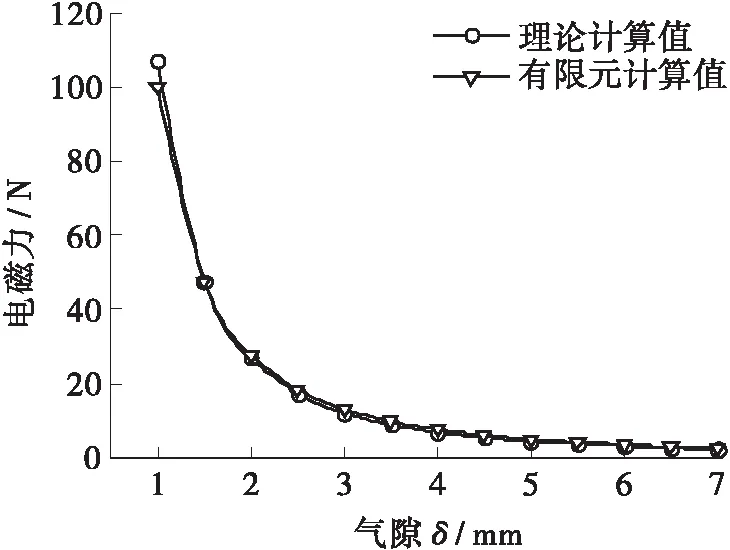
图9 电磁力随气隙的变化曲线
3 主动吸振器的力特性分析
主动吸振器是在电磁力的作用下对主系统施加驱动力,因此电磁力特性直接影响到主动吸振器的驱动力特性。为了评估以电磁铁为作动器的主动吸振器驱动力特性,有必要对主动吸振器的输入(交变电流)与输出(驱动力)关系进行研究。
(13)
将式(13)代入式(2),可得主动吸振器动质量的运动方程为
(14)
δ=δ1+x2
(15)
上式中δ1为动铁心下表面与静铁心上表面之间的初始气隙。对式(14)进行求解,分析主动吸振器的驱动力特性。仿真参数如表1所示,表中参数为主动吸振器设计的目标参数。
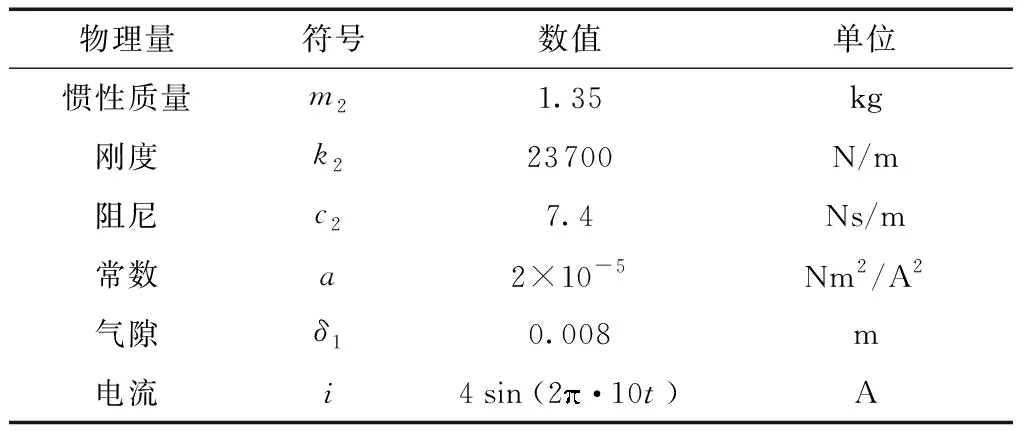
表1 主动吸振器仿真参数
3.1 电磁力与交变电流的关系
(16)
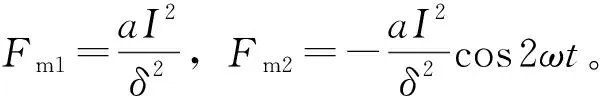
由图10可知电磁力Fm≥0,即主动吸振器通电工作时,其动质量m2受到单向的电磁力作用,动质量在初始静平衡下受到电磁力直流分量Fm1的作用而向下运动,给橡胶弹簧施加了一个预紧力,同时动质量在交变分量Fm2的作用下进行往复运动。
3.2 主动吸振器的驱动力特性
主动吸振器在电磁力的交变分量Fm2的作用下进行往复运动从而产生驱动力,动质量运动微分方程为
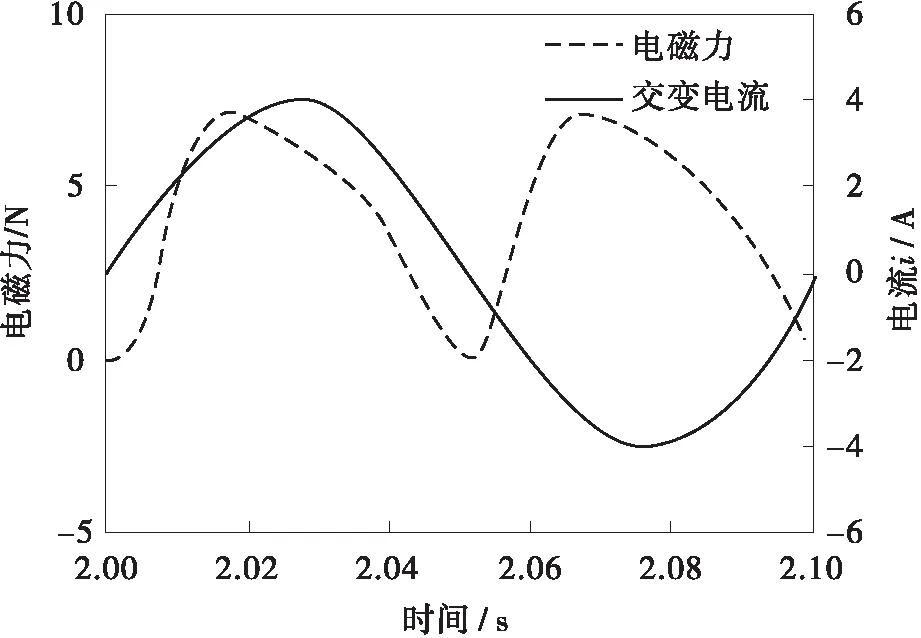
图10 电流i与电磁力Fm时域曲线
(17)
结合式(3)计算稳态下的驱动力,结果如图11所示。
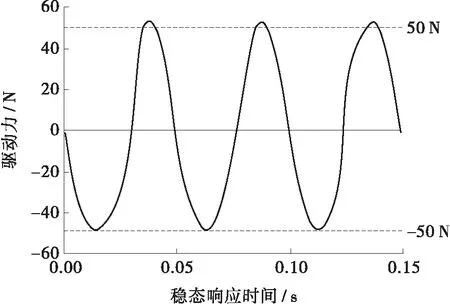
图11 驱动力的时域稳态响应
从图11可以看出,主动吸振器表现出周期性的驱动力特性,但驱动力峰值和谷值存在一定的差异。这是因为:主动吸振器通电工作时,由动铁心和线圈构成的动质量位移发生变化,导致气隙δ改变,从而引起电磁力幅值改变;由于主动吸振器受到变化的电磁力作用,导致驱动力的峰谷幅值不相等。当动质量向下运动时,气隙减小,电磁力幅值增大;动质量向上运动时,气隙增大,电磁力幅值减小。
3.3 驱动力偏差对主动吸振器减振效果的影响
理想条件下,主动吸振器施加的驱动力与主系统受到的激励力幅值、频率相等且反相时,理论上可实现完全减振。但在实际中,由于受到控制精度、系统迟滞等影响,电磁式主动吸振器施加的驱动力与理想驱动力不可避免存在一定的偏差,包括幅值差、相位差和频率差。为给控制系统的设计提供参考,理论分析主动吸振器驱动力偏差对减振效果的影响,并通过搭建简支平板减振试验台,对理论分析结果进行试验验证。
3.3.1 幅值差对减振效果的影响

(18)
式中:X0为未安装主动吸振器时主系统的稳态响应位移幅值;X1为主动吸振器工作时主系统的稳态响应位移幅值。
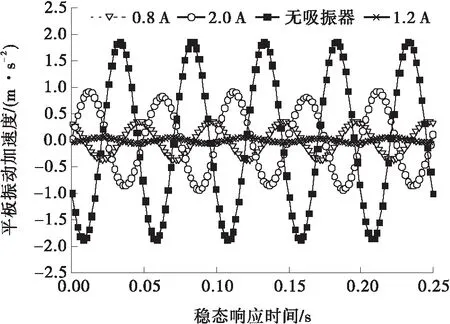
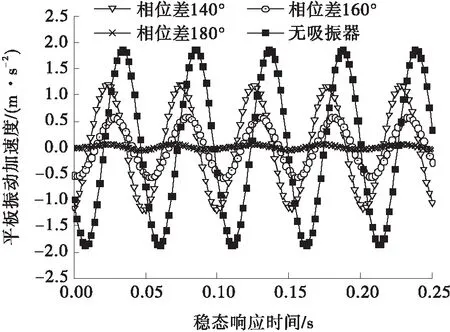
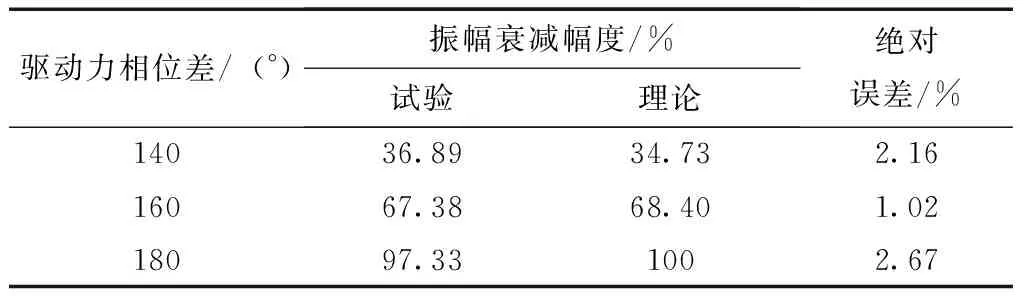
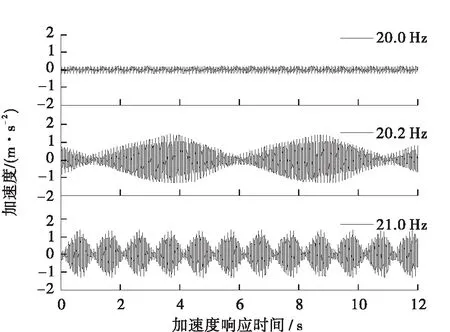
当Fd=F1时,β=0,此时主动吸振器驱动力与主系统所受激励力完全抵消;当0 为了观察不同的幅值差对主动吸振器减振效果的影响,搭建了如图12所示的试验台。激振器5通过激振器顶杆6对钢质平板2施加垂向正弦力激励(激励频率为20 Hz),平板在激励力的作用下发生振动。通过给电磁式主动吸振器提供交变电流,主动吸振器对平板施加与激励力同频率、反相的驱动力。 图12 试验台简图 1—加速度传感器;2—钢质平板;3—橡胶弹簧;4—底座; 5—激振器;6—激振器顶杆;7—主动吸振器 由于试验中主动吸振器的驱动力不便于测量,而驱动力幅值与交变电流有效值成正比,因此在分析不同驱动力幅值差对减振效果的影响时,驱动力幅值差用实际通入电流有效值与理想电流有效值的偏差来代替。试验中,对主动吸振器分别通入有效值为0.8、1.2及2.0 A的交变电流,并利用LMS数采设备采集平板的振动加速度,结果如图13所示。 图13 不同电流有效值下平板振动加速度响应 Fig.13 Vibration acceleration response of the flat under diffE-rent current effective value 由图13可见,当主动吸振器通入有效值为1.2 A的交变电流时,平板振动加速度幅值为0.05 m/s2,与未安装主动吸振器时平板振动加速度幅值(1.87 m/s2)相比衰减了97.33%,平板振动几乎完全衰减,并认为主动吸振器在该电流有效值下的驱动力为理想驱动力;当电流有效值为0.8 A时,平板振动加速度幅值为0.36 m/s2,衰减了80.75%;当电流有效值为2.0 A时,平板振动加速度幅值为0.89 m/s2,衰减了52.41%。可知主动吸振器的减振效果随着驱动力的幅值差的增大而变差。 3.3.2 相位差对减振效果的影响 (19) 通过试验观察了不同相位差对主动吸振器减振效果的影响。分别进行了3种工况(相位差为180°、160°及140°)下的试验研究。试验中,激振器对平板施加频率为20 Hz的简谐力激励,并通过给主动吸振器提供有效值为1.2 A的交变电流,保证驱动力与激励力具有相同的幅值和频率,平板的振动加速度响应如图14所示。 图14 不同相位差下平板振动加速度响应 Fig.14 Vibration acceleration response of the flat under different phase variance 从图14可知,未安装主动吸振器时平板振动加速度幅值为1.87 m/s2,当主动吸振器对平板施加相位差为180°的理想驱动力时,平板振动加速度幅值衰减到0.05 m/s2,振幅衰减了97.33%;当相位差为160°时,平板振动加速度幅值为0.61 m/s2,衰减了67.38%;当相位差为140°时,平板振动加速度幅值为1.18 m/s2,衰减了36.89%。 将试验测得的平板振动加速度衰减幅度与理论计算结果进行对比,如表2所示。由表2可见,试验结果与理论计算结果基本吻合,最大误差为2.67%。结果表明,随着相位差逐渐偏离180°,主动吸振器对平板的振动控制效果也逐渐变差。 表2 不同相位差下的减振试验结果与理论计算结果对比 Table 2 Comparisons of response of the primary mass obtained from the analytically model with the measured data 驱动力相位差/(°)振幅衰减幅度/%试验理论绝对误差/%14036.8934.732.1616067.3868.401.0218097.331002.67 3.3.3 频率差对减振效果的影响 F=F1sinω1t+F1sin(ω2t+φ2) (20) 令主系统稳态位移响应为 (21) (22) (23) 为了验证上述的 “拍”振现象,进行了试验研究。利用激振器对平板施加频率为20 Hz的简谐力激励,通过给主动吸振器提供有效值为1.2 A的交变电流,并使主动吸振器对平板施加频率分别为20.0、20.2、21.0 Hz的驱动力。主系统的振动加速度响应如图15所示。 图15 不同频率差下平板振动加速度响应 Fig.15 Vibration acceleration response of the flat under diffE-rent frequency variance 由图15可知,当主动吸振器施加的驱动力无频率差时,减振效果显著;当存在频率差时,平板将产生 “拍”振现象,这使得平板的振动得不到有效控制。 (1)以电磁铁为作动器,提出了一种新型电磁式主动吸振器结构;推导了该主动吸振器作动器的电磁力数学模型,并对电磁力进行了有限元仿真,验证了电磁力数学模型的正确性。 (2)基于推导的电磁力数学模型,建立了该电磁式主动吸振器的运动学方程,并对其力特性进行了分析,结果表明:在交变电流的励磁下,主动吸振器产生交变的电磁力,且交变电磁力频率为交变电流频率的两倍;在交变电磁力的作用下主动吸振器产生简谐驱动力,且由于作动器电磁力的非线性,导致了主动吸振器驱动力幅值表现出峰、谷值不相等的特征。 (3)理论研究了主动吸振器产生的实际驱动力与理想驱动力之间存在偏差时对减振效果的影响,并搭建了简支平板减振试验台,通过试验验证了在不同驱动力幅值差、相位差及频率差下,主动吸振器对平板振动抑制的效果。结果表明:当实际驱动力与理想驱动之间的幅值差、相位差逐渐增大时,主动吸振器的振动抑制效果亦逐渐减弱;当存在频率差时,无论偏差大小,平板均产生“拍”振现象,主动吸振器对其振动不能进行良好控制。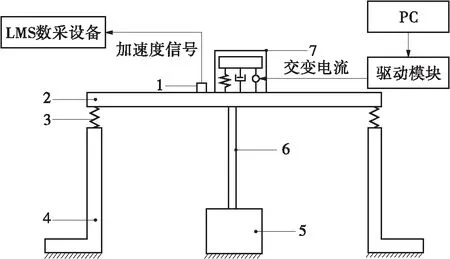




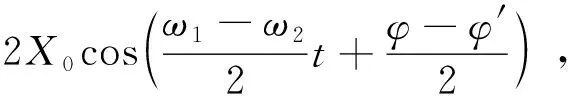

4 结论
