基于高阶动态贝叶斯网络嵌入的路面异常检测算法

李博 张洪刚

(北京邮电大学 信息与通信工程学院，北京 100876)

近年来我国公路运输行业发展迅速，巨大的交通流量使得对路面状况的要求不断提高，方便快速地进行路面异常检测受到越来越多的关注。及时发现路面异常有助于保证路面质量、降低交通事故的发生率、避免或缓解交通拥堵、节约油耗、降低污染、提高辅助驾驶和自动驾驶体验，对保障生命安全、提高出行效率、节能减排有着深远意义[1- 2]。

通过摄像头采集路况数据，模型易受摄像头参数、拍摄角度、光照、实际路况等影响[3- 5]；相比之下，通过控制器局域网络(CAN，Controller Area Network)/ 车载诊断系统(OBD，On-Board Diagnostic)[6- 8]、手机传感器等设备采集数据更加方便[9]，并且基于传感信号数据构建的模型更稳定，利于普及和推广。通过对传感数据的处理和分析实现异常检测有两种常见方案。一种方案是基于原始信号计算的统计度量来进行异常检测，文献[10]通过对加速传感器信号统计度量的计算和适当阈值的选取，实现异常路面的检测；Oneyama等[11]通过传感信号的FFT(Fast Fourier Transform)特征，对路面状况实现了分级；文献[12]认为路面的颠簸程度与加速传感数据和速度传感数据存在一定的线性关系；文献[13]提出一种基于多传感器信号进行路面不平程度测量的方法。另一种方案是将异常检测问题转化为分类问题，在近几年取得了更好的效果，Chen等[14]利用正常路面和异常路面传感信号分布上的差异，构建GMM(Gaussian Mixture Model)模型实现路面异常检测；文献[15-16]利用手机中的GPS和加速传感器等传感设备定频收集信号数据，作为SVM等分类器的特征输入，实现了正常路面和异常路面的区分；Silva等[17]对比了Gradient Boosting、MLP Classifier、Gaussian NB、Linear SVC等方法的检测效果；Carlos等[18]对比了SVM与几种经典统计度量方法的检测效果。上述研究中，对模型的时序性和不同传感器信号之间的时序相关性讨论较少。另外，异常路面对传感信号产生的影响，呈现在不同的尺度，也加大了传感信号分析的难度。

本研究给出了一种针对传感器信号时间序列数据进行路面异常检测的算法，通过相关性分析和Granger因果检验构建初始的动态贝叶斯网络[19]；然后利用小波分解将时序数据在不同位置和尺度展开，解决传感器信号的尺度分析问题，通过卷积神经网络(CNN，Convolution Neural Network)对高阶网络节点进行网络嵌入(NE，Network Embedding)学习[20- 23]；基于网络嵌入进行链路预测，结合代价敏感的MDL(Minimal Description Length，最小描述长度)，解决高阶时序相关性的分析问题，修正了网络结构，完成分类器构建；最后通过实验对检测效果进行了验证。

1 路面异常检测模型框架

1.1 基于动态贝叶斯网络的检测模型

通过对网络结构和网络概率参数的学习构建动态贝叶斯网络分类器，然后用分类器来对路面情况进行分类。

贝叶斯网络可以较好地描述信号间的依赖关系，动态贝叶斯网络在传统贝叶斯网络的基础上引入随时间变化的马尔科夫模型的思想，解决了时序信号间相关性的描述问题。文中，以获取的速度传感器值(Speed)、加速度传感器值(Acc)、陀螺仪传感器值(Gyro)等传感器信号数据构建的网络结构进行示意说明，如图1所示。图1(a)是初始时刻网络，图1(b)是转移网络，通过图1(a)与1(b)的结合，可以得到如图1(c)所示的动态贝叶斯网络。设ci为待预测类别变量，xt，n代表第t个时刻第n个传感器采集到的传感信号数据，则有：

p(ct|xt，1，…，xt，n，xt-1，1，…，xt-1，n，ct-1)=

(1)

其中，p(xt，1，…，xt，n，ct，xt-1，1，…，xt-1，n，ct-1)可以通过类ct-1的先验概率p(ct-1)、t-1时刻的条件概率p(xt-1，1，…，xt-1，n|ct-1)以及不同时刻转移概率p(ct|ct-1)p(xt，1，…，xt，n|ct，xt-1，1，…，xt-1，n，ct-1)计算得出。

按式(1)计算各路面状况分类的概率，选取最大概率对应的路面类别为预测类别，并可以将一阶动态贝叶斯网络推广至高阶[19]，进而在多个时间点上进行时序分析。贝叶斯网络可以描述节点间的相互关系，具有较强解释性。动态贝叶斯网络可以通过转移网络描述多个时刻节点间的关系，从而挖掘传感信号在多个时刻间的关联关系。

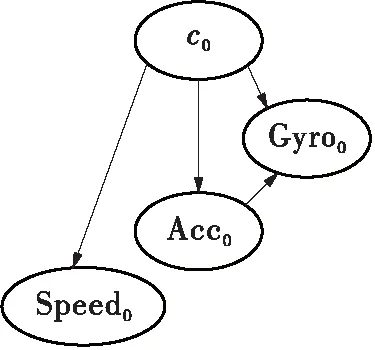
(a)初始时刻网络

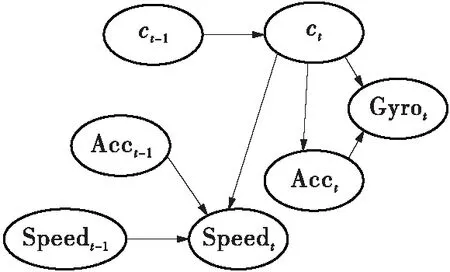
(b)转移网络

(c)动态贝叶斯网络

1.2 检测模型的学习框架

从传感器数据中直接学习到一个精准的路面异常检测模型具有较大难度，首先要计算出一个初始网络模型，然后通过对网络迭代修正，生成较为精准的路面异常检测模型。本研究提出的路面异常检测模型的学习框架如图2所示，学习过程被划分为动态贝叶斯网络初始化和网络修正两部分。模型的整体学习过程为：以多变量时序传感器数据作为训练数据输入，进行网络初始化，然后迭代进行网络修正，直至最大迭代次数或收敛条件后输出模型。

网络初始化部分又分为结构初始化和参数学习，其中结构初始化包括初始时刻网络初始化和转移网络初始化。文中提出使用相关性分析和Gran-ger因果检验方法，分别分析初始时刻和一阶时序线性相关传感信号的依赖关系，依据依赖关系构建初始化结构，然后根据网络结构进行参数学习生成初始化网络。

网络修正部分包括网络嵌入学习、结构修正和参数学习。文中提出使用网络嵌入学习来分析传感信号间复杂的高阶时序相关性，在初始化网络的基础上生成网络嵌入。获取网络嵌入后，基于网络嵌入进行链路预测(Link Predication)，结合MDL实现网络结构修正。对修正后的结构重新进行参数学习，如果未达到迭代次数或收敛条件，则进行下一轮网络修正。

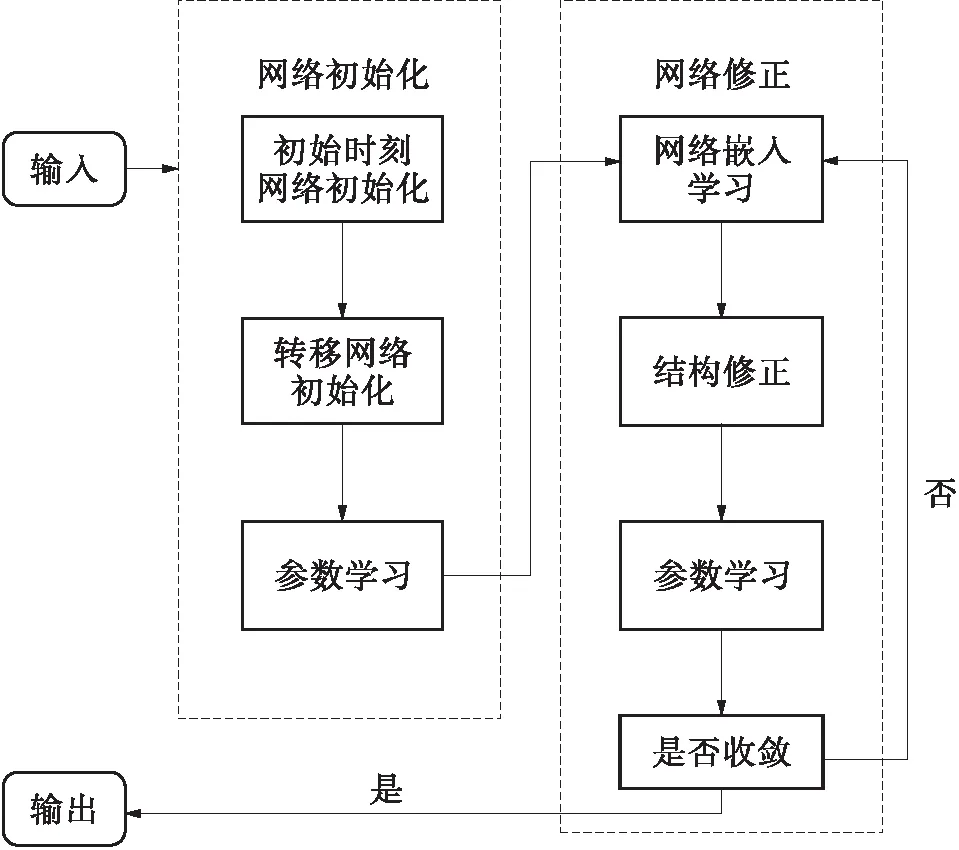
图2 路面异常检测模型训练过程

2 网络初始化

2.1 初始时刻初始化

初始时刻网络结构的学习，目的是发现各传感器信号与预测类别之间在同一时刻的相关性，为后续优化提供结构基础。首先计算各传感器信号与类别变量的Pearson相关系数，以得到较为明显的关联关系。

(2)

式(2)为传感器信号时间序列X与类别标注Y的相关性系数。假设X={x1，x2，…，xm}，Y={y1，y2，…，ym}，m为传感器信号样本数量，可得式(3)：

(3)

式(3)的绝对值在一定程度上反映了两个序列的相关性。实践中认为，当该值在[0.6，0.8]范围内时两序列强相关，当该值在[0.8，1.0]范围内时两序列极强相关。这里以0.6为阈值，生成传感器信号X节点到类别Y节点的边界。确定贝叶斯网络结构后，使用极大似然估计法(Maximum Likelihood Estimation，MLE)求解概率参数。该方法简便有效，但只能判别传感器信号与类别节点间所具有的线性关系，因此需要在网络修正阶段进一步优化网络。

2.2 转移网络初始化

转移网络的学习，目的是发现各传感器信号间在相邻时刻的相关性。Granger因果检验是一种可以在时序上计算变量相关性的技术[24]。车传感信号是多变量的时序信号，且在时序上有相关性(比如速度和加速度信号)，因此符合Granger因果检验的适用范围。这里通过Granger因果检验实现转移网络结构的初始化，用以分析两个临阶网络之间在时序上的转移关系。如果由传感器信号值yk和传感器信号值xk滞后值所决定的yk的条件分布，与仅由yk滞后值所决定的条件分布相同，即

f(yk|yk-1，yk-2，…，xk-1，xk-2，…)=

f(yk|yk-1，yk-2，…)

(4)

则认为传感器信号X对传感器信号Y不存在Granger因果性关系。实际计算中，将其等价于其它条件不变时，若加上传感信号X的滞后变量后对Y的预测精度不存在显著性改变，则认为X对Y不存在Granger因果性关系。该问题可以转化为两个线性回归的检验问题。

(5)

(6)

其中，αi和βj是式(5)和式(6)两个线性回归模型的回归系数。通过F统计完成其检验。构建传感信号X对Y不存在Granger因果性关系的假设：

H0：β1=β2=…=βk=0

(7)

如果X的滞后变量回归参数估计值全部不存在显著性，则上述假设不能被拒绝。该检验计算出前后两个时刻的传感信号关系，再结合相关系数计算出的相同时刻传感信号和类别间的关系，得出转移网络结构，然后使用MLE对网络参数初始化。时序信号间的高阶非线性关系需要在网络修正过程中分析。

3 网络修正学习

3.1 网络嵌入的学习目标

传感器信号由于复杂的路面作用，常呈现非线性相关和高阶时序相关，这种复杂的相关性不容易在网络初始化过程中获取。网络修正学习，目的是基于初始网络，对这种高阶非线性关系进行学习，对网络进行优化。文中提出使用网络嵌入进行高阶贝叶斯网络修正。网络嵌入可以在初始网络中学习到更为深层次的节点之间的关联关系，并且可以通过不断迭代学习达到较优的修正结果。

对高阶贝叶斯网络结构进行优化，将H阶贝叶斯网络作为待更新网络，使用上下文敏感的网络嵌入学习方法[23]。假设G=(V，E，S)是待更新网络，其中V是信号节点集合，E⊆V×V代表节点之间的边集合，S代表传感器信号节点的时间序列。其中，ωu，v是eu，v∈E的权重。将节点v∈V对应的传感器信号时间序列表示为sv，nv=|sv|为传感器信号数量。根据网络结构和节点对应的传感器信号时间序列对每个节点计算上下文敏感的向量，即对于一条边eu，v生成两个向量v(u)∈Rd和u(v)∈Rd(R是实数集)。

针对网络结构和传感器信号时间序列数据，构建两种向量：对于节点v，分别构建基于结构的向量vs和基于传感信号时序数据的向量vt。其中，vs用于捕捉待修正网络的结构信息，vt用于结合对应传感器信号的时间序列优化网络结构。该向量是上下文敏感的，即参与计算的边所对应的两个节点不同，则计算的向量结果也不同。设v=vs⊕vt，其中⊕表示将两个向量进行拼接。最大化各边的总目标函数：

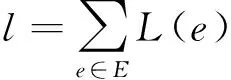
(8)

其中，L(e)是每条边的目标函数，可以表示为

L(e)=Ls(e)+Lt(e)

(9)

这里，Ls(e)表示基于待修正网络结构的目标函数，Lt(e)表示基于传感器信号时间序列的目标函数。

贝叶斯网络中的边是有向的，以有向边的对数似然来定义Ls(e)：

Ls(e)=ωu，vlgp(vs|us)

(10)

将式(10)的条件概率定义为

(11)

通过定义Lt(e)来进一步分析高阶时序传感信号间的非线性关系。

Lt(e)=α×Ltt(e)+β×Lts(e)+γ×Lst(e)

(12)

其中：α、β和γ为权重，

Ltt(e)=ωu，vlgp(vt|ut)

(13)

Lts(e)=ωu，vlgp(vt|us)

(14)

Lst(e)=ωu，vlgp(vs|ut)

(15)

式(13)-(15)中的条件概率形式上与基于结构的条件概率定义相似，将两种节点向量映射到同一表达空间。式(13)-(15)可通过式(11)计算得出。

3.2 时序信号数据小波分解

缓速带、坑洼和颠簸等路面对陀螺仪等传感器信号产生了不同尺度的频域影响，单纯从时频分析信号，不易发掘频域中蕴含的特征，这里引入小波技术对传感器信号进行分析。小波变换可以同时分析传感器信号时域和频域的不同尺度特征[25]。首先对传感器信号作小波变换，给定尺度函数φ(x)和小波函数ψ(x)，信号时间序列函数f(x)可以展开为不同尺度不同位置的尺度函数和小波函数的线性组合：

(16)

其中：

(17)

(18)

称c0(k)为近似系数，dj(k)为细节系数。

φj，k(x)=2j/2φ(2jx-k)

(19)

ψj，k(x)=2j/2ψ(2jx-k)

(20)

其中，k为位置系数，j为尺度阶数，j越大，尺度越小。对原信号函数进行高阶分解：

(21)

对于给定eu，v，两个传感器信号节点所对应的时间序列为su和sv，通过小波分解将时序序列划分为矩阵p∈Rd×m和Q∈Rd×m(R是实数集)作为CNN的输入，其中m取值为小波分解级数加2，矩阵由小波分解的0阶近似和0至m-2阶细节参数构成。通过CNN来实现上下文敏感的时间序列嵌入向量计算。

3.3 上下文敏感网络嵌入学习

路面异常造成的传感信号变化具有局部连续性和多信号变量间的关联性，CNN可以通过局部连接和权值共享来描述这些特点，这里通过CNN来实现传感信号上下文敏感的网络嵌入学习[23]。上下文敏感的网络嵌入学习过程如图3所示。令A∈Rd×d(R是实数集)为两个时间序列小波变换后的卷积矩阵，则相关性矩阵F∈Rm×n可以表示为：

F=tanh(PTAQ)

(22)

其中，F中的每一个元素Fi，j代表两个隐向量Pi和Qj的相关性得分。基于上述计算，对F的行和列分别构建池化层，将其定义为

(23)

(24)

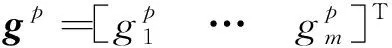
通过Softmax函数将向量gp和gq转化为上下文相关度向量ap和aq。ap中的第i个元素定义如下：

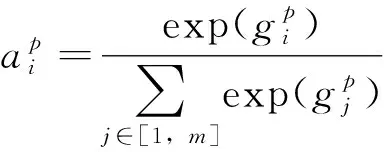
(25)

上下文嵌入向量定义为

(26)

(27)

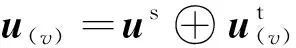
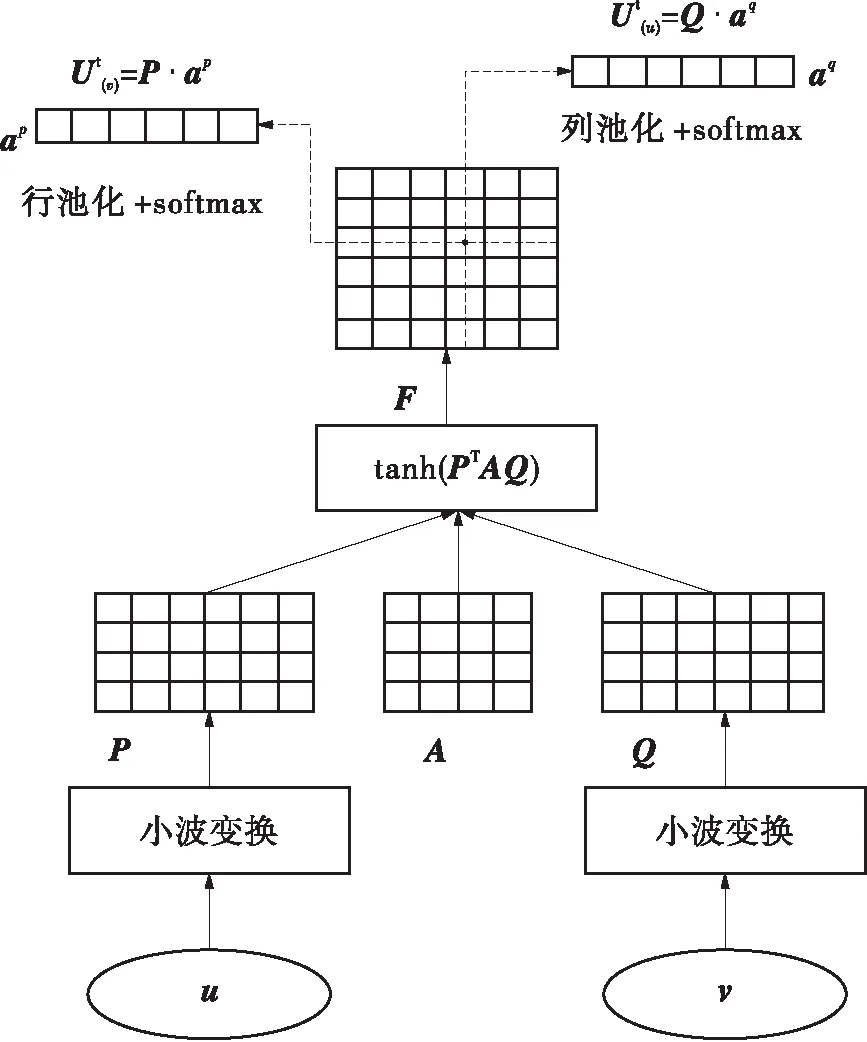
图3 小波上下文敏感网络嵌入

3.4 网络结构修正

为了对比评价修正前后的网络结构，需要确定结构评分标准，这里提出在传统评分标准MDL[19，26]中加入代价敏感系数，以解决数据集中异常类别道路占比较小的问题。假设使用某模型对信号数据集合Z进行压缩存储，设随机变量U={x1，x2，…，xn}的贝叶斯网络结构为Bs=(U，E)，其中U为贝叶斯网络的节点集合，E是有向边的集合。Bp={p(xi|parent(xi))：xi∈U}为条件概率表(Conditional Probability Tables，CPTs)的集合，parent(xi)是网络结构中xi的父节点集合，则p(xi|parent(xi))为传感器信号节点xi在其父节点某一取值组合状态下的条件概率分布。网络结构Bs的DL测度为

DL(Bs：Z)=DLBN(Bs∶Z)+DLdata(Z|Bs)=

DLstru(Bs)+DLtab(Bs)+DLdata(Z|Bs)

(28)

其中，DLBN(Bs：Z)=DLstru(Bs)+DLtab(Bs)为压缩模型的编码长度。对式(23)加入分类代价敏感系数C，对正类和负类错分样本进行加权惩罚。

(29)

H(x|parent(xi))=

-∑p(x，parent(xi))lgp(x，parent(xi))

(30)

式(30)为条件熵，可通过对Z中实例个数统计求出。

(31)

式(31)为压缩模型中网络结构的编码长度，|pai|表示|parent(xi)|中节点取值的组合数目， 即节点xi的父节点取值的组合数目。

(32)

式(32)为压缩模型中条件概率表的编码长度，|xi|表示节点xi的取值数。

算法1：动态贝叶斯网络结构优化算法

Input：待优化贝叶斯网络结构Bs

计算Bs的代价敏感MDL得分Score

Fori=1to MaxTurn do

网络嵌入学习计算边的l集合

从集合中选取l最大值对应的边

Ifev，u在网络Bs中不存在 then

添加从v到u的边，生成新B′s；

放弃修改

Else

计算

If Scorenew≤Score，then

放弃修改

Else

Score=ScorenewEndif

Endif

Endif

从集合中选取l最小值对应的边ev′，u′

Ifev′，u′已经在网络存在 then

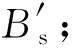
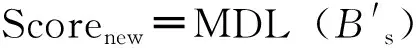
If Scorenew≤Score，then

放弃修改

Endif

Endif

Endfor

网络结构评估算法结合网络嵌入链接预测和MDL构建了搜索算法。以代价敏感的MDL准则评估模型结构，DL测度越小，代表贝叶斯网络结构越可能合理。

基于算法1，完成一次对待优化贝叶斯网络的修正，算法输入是H阶贝叶斯网络。优化初始时刻的网络结构：将初始时刻的网络结构与当前转移网络组成H阶贝叶斯网络，仅优化初始时刻网络部分的边，然后从优化后的网络中拆分初始时刻贝叶斯网络结构。优化转移网络：直接以H阶贝叶斯网络转移网络作为输入进行优化。对优化后的网络结构，重新使用MLE学习网络概率参数。

4 实验评估

使用MMSys2017中提出的Multimedia Sensor Dataset作为实验数据集。该数据集通过手机传感器收集了多种信号数据，包括GPS、加速度、方向、磁场和陀螺仪等传感器信号数据，以及用于辅助标注的视频数据，并在数据对齐、速度数据生成、数据准确度校正方面进一步处理。

该数据集提供了3种异常路面数据：Pothole Passing、Speed Bump Passing、Uneven Road Passing。通过视频辅助，对行驶过程中的异常路面时间进行标注，将数据集分为3种异常路面采集的信号数据和正常路面采集的信号数据，作为监督学习的训练数据和评估过程的测试数据。实验中将数据以10s为时间窗口切分成样本。针对不同路面数据集进行多组实验，结果如表1所示。这里使用几种不同的评估指标[15- 18]，正确率是指正确分类的样本占总样本的比例，除正确率外，其它各项评估参数定义如下：

(33)

(34)

(35)

(36)

(37)

误检率高，会使正常路面更容易被误判为异常路面。漏检率高，会使异常路面更容易被误判为正常路面。F1是综合评定指标，代表该方法性能的综合表现，F1值高，表示异常道路检测结果较为准确，并且对异常道路的召回也比较理想。

实验对比中，选取了一些有代表性的利用传感信号进行路面异常检测的方法：基于统计度量的方法Z-DIFF[10，18]和STDEV[18]，基于传统机器学习的方法SVM[15- 16]和GBDT[17]。另外，还选取了一些时序分类方向的前沿模型(如：基于1-NN的1-NN(ED)和1-NN(DTW)方法[27]，基于神经元网络的MLP[28]和MC-DCNN方法[27]，基于信号形状的Shapelets-DT方法[29]以及分析信号间时序关系的贝叶斯网络方法BN[26]和DBN[19])，用于对比文中方法。

从不同数据集角度来观察实验结果，整体上看各种方法对Uneven Road Passing的检测效果差于Pothole Passing和Speed Bump Passing，Uneven Road路段标注难度较大，异常路段与正常路段频繁交错出现，难以精准区分。各种方法对Speed Bump的检测效果相对较好，一般车辆经过该路面时会提前准备，例如适当减速，并且经过过程中车辆震动相对剧烈，多项传感器信号变化较为明显。

对各体系内方法进行内部对比，基于统计度量的方法，Z-DIFF较STDEV有更高的正确率和更低的误检率，但漏检率并不稳定；基于传统机器学习的方法，GBDT与SVM相比在正确率、漏检率、误检率和F1值几项指标方面，在不同数据集中结果较为接近，不存在明显优势；基于1-NN的方法，1-NN(DTW)较1-NN(ED)具有更低的漏检率和误检率；基于神经元网络的方法，MC-DCNN较之MLP，各项评估指标表现更好；基于贝叶斯网络的方法中，文中方法较传统的BN和DBN在各项评估指标方面表现更好。

对不同方法体系进行对比，基于统计度量的方法和传统机器学习方法表现较差，尤其体现在F1值方面，较其它方法体系有明显差距。而时序分类方法整体效果上表现更优，证明文中考虑利用信号时序特点构建分类模型的可行性，以及较传统方法的优越性。在时序分类方法中，基于信号形状的方法表现较差，基于1-NN的方法和基于神经网络的不同方法表现有所差异，基于贝叶斯网络方法表现偏好，信号间时序相关性可以被贝叶斯方法更好地学习和表现。

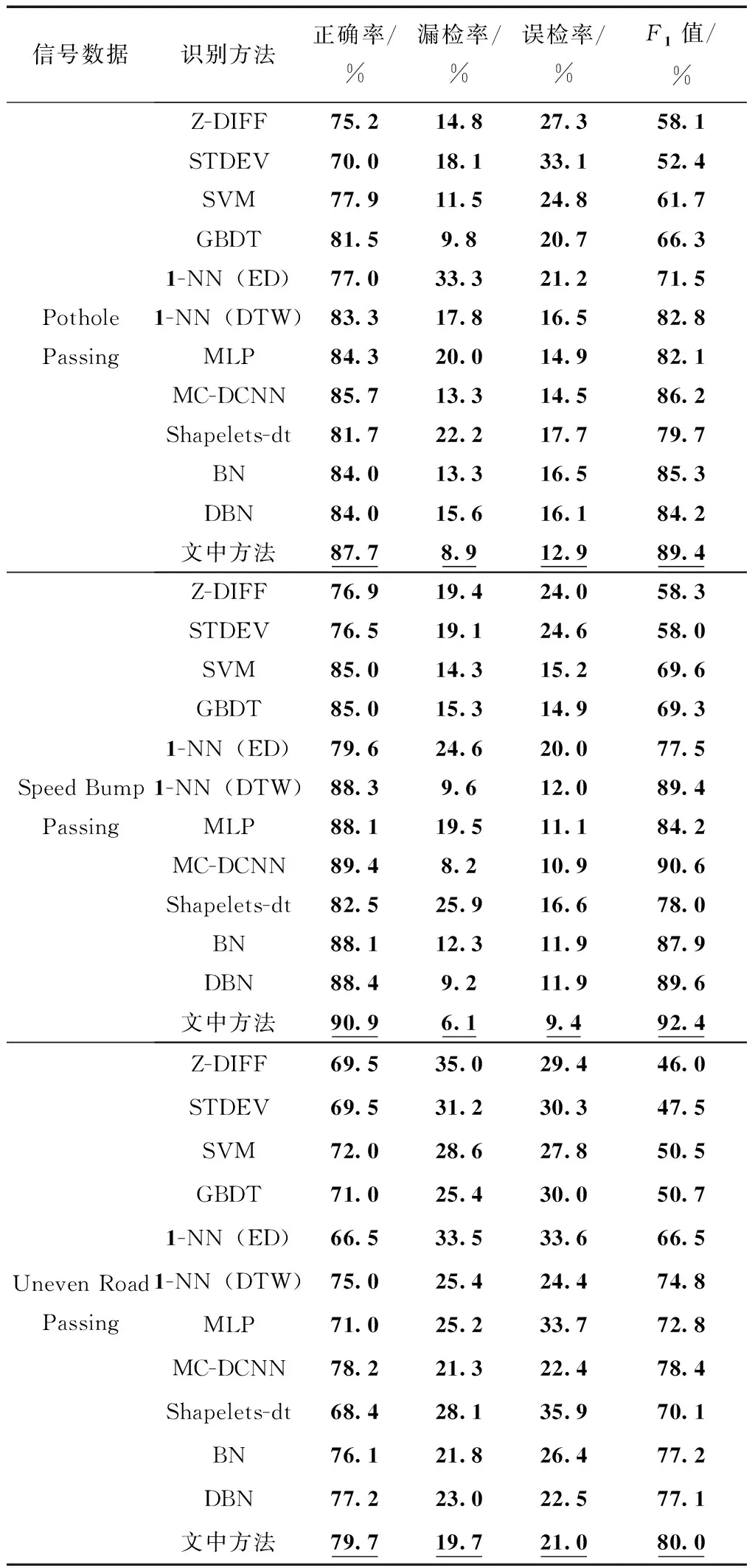
表1 不同数据集识别结果

对各方法在各数据集上进行对比，在Pothole的检测上，文中方法对比其它方法，在正确率上至少提高2个百分点，最多可以提高17个百分点；在漏检率上至少降低近1个百分点，最多可以降低24个百分点；在误检率上至少降低1.6个百分点，最多可以降低20个百分点。在Speed Bump的检测上，文中方法对比其它方法在正确率上最少可以提高1.5个百分点，最多可以提高14个百分点；在漏检率上至少降低2个百分点，最多可以降低近20个百分点；在误检率上至少降低1.5个百分点，最多可以降低11个百分点。在Uneven Road的检测上，文中方法对比其它方法在正确率上最少可以提高1.5个百分点，最多可以提高13个百分点；在漏检率上至少降低1.6个百分点，最多可以降低15个百分点；在误检率上至少降低1.4个百分点，最多可以降低14个百分点。在F1值上，文中方法在3种数据集上可以达到80%以上，其中对Speed Bump的识别达到90%以上。同时，文中方法在不同的数据集实验中，各项评估指标能稳定在一个较好的状态，在实际应用环境中具有更好的鲁棒性。

5 结语

路面检测在更好地辅助驾驶、提高驾驶员和行人安全等方面有重要意义。本研究提出一种基于高阶动态贝叶斯网络嵌入的路面异常检测算法，该算法将路面检测问题转化为时序信号数据分类问题，通过构建动态贝叶斯网络分类器解决检测问题。首先，提出利用相关性分析和Granger因果检测分别分析同一时刻和不同时刻的传感器信号与道路类型间的相关性，以构建初始网络结构；然后，提出将信号数据进行小波变换以分析不同尺度下的路面信号特征，并通过CNN对多尺度的传感信号数据的局部连续性进行分析，进而实现嵌入学习以分析高阶时序信号之间的相关性；最后，结合网络嵌入和代价敏感的MDL完成网络修正，提出一种高阶网络结构优化算法。组建不同路面状况的数据集，对基于统计度量的方法、基于传统机器学习分类模型的方法、基于1-NN、基于形状、基于神经元网络和贝叶斯网络的时序数据分类方法进行对比，结果表明文中方法具有更低的误检率和漏检率、更高的正确率和F1值，并且在不同数据集上的表现效果更加鲁棒。