基于跨尺度随机游走的立体匹配算法

李锵 段子阳 张一帆 朱程涛

(1．天津大学 微电子学院，天津 300072；2.中国科学技术大学 中国科学院空间信息处理与应用系统技术重点实验室(联合)，安徽 合肥 230027)

立体视觉是从两个或多个视点观察同一景物，以获取在不同视角下的感知图像；通过三角测量原理计算图像像素点间的视差来获取景物的三维信息[1]。现阶段，该技术已广泛应用于机器人导航、无人驾驶、虚拟现实、三维重建等领域[2]。立体视觉技术主要涉及摄像机标定、图像预处理、立体匹配、三维重建等步骤。立体匹配是其中最重要也是最困难的步骤，其主要目的是通过相应的算法获取参考图像与目标图像之间对应匹配点间的关系，生成相应的视差图，依据视差图信息及三角测量原理即可得到场景的深度信息。

Scharstein等[1]将立体匹配算法分为4个步骤：匹配代价计算、代价聚合、视差计算、视差求精。立体匹配算法通常被分为局部算法和全局算法。局部算法通常采用基于窗口滤波的方式实现匹配，Yoon等[3]提出一种自适应支持权重算法，该算法根据窗口内每个像素与中心像素的颜色相似性、距离相似性进行权重分配，其本质是一种双边滤波的过程，可以有效保护边缘深度信息，但运算复杂度较大；Hosni等[4]提出用引导滤波代替双边滤波的局部算法，该算法在降低算法复杂度的同时提升了匹配精度；Yang等[5]提出一种半局部代价聚合方法，将整幅图像作为核函数窗口，利用最小生成树进行代价匹配；Mei等[6]先对图像进行分割，后采用半局部方法对每个分割块求取子树，然后根据贪心算法，将各个分割对应的子树进行合并；Hamzah等[7]提出迭代引导滤波用于代价聚合过程，以保持和改善图像边缘信息；Williem等[8]使用深度学习来执行自引导滤波过程，不需要任何引导图像进行监督。局部算法具有计算简单、速度快、能进行图像实时处理的优点，但由于缺乏对视差关系的合理约束导致算法在低纹理区域、遮挡区域的匹配精度不高。

全局算法通过在能量方程中引入视差约束惩罚项，能有效处理低纹理区域及遮挡区域的匹配问题。目前常用的全局算法有图割算法(Graph Cut，GC)[9]、置信传播(Belief Propagation，BP)[10]、动态规划(Dynamic Programming，DP)[11]等。基于图割和置信传播的立体匹配算法需要大量的计算资源，计算复杂度高，实时性较差。Shen等[12]首先将随机游走算法(RW)应用于立体匹配中，该算法能够产生精确的全局函数最优解；Jin[13]等提出了改进的重启动与随机游走算法(ARW)，该算法能在相对较低的计算复杂度下得到高精度的匹配结果。

传统的立体匹配算法大多是建立在单尺度模式下，Zhang等[14]提出跨尺度的局部算法，该算法模拟人眼视觉系统采取由粗到细(Coarse to Fine)的策略融合多尺度图像信息用于匹配，实现了立体匹配算法由单尺度向多尺度的转变，提升了立体匹配的精度；Liu等[15]提出Census变换与多尺度空间结合的立体匹配算法，提高了在弱纹理区域和视差不连续区域的匹配精度。

传统的跨尺度算法未能有效考虑邻近点之间的视差约束关系，致使算法在低纹理及遮挡区域的匹配精度有限。为了提升上述区域的精度，本研究充分结合多尺度以及全局算法的优势，首先用中心对称的Census变换和梯度信息相结合来计算多尺度下的匹配代价；然后利用超像素分割[16]分别对各尺度下的图像进行分割，并在分割区域内进行匹配代价聚合，再利用重启动与随机游走算法进行全局上的优化；最后，利用正则化约束进行多尺度匹配代价融合，以实现高精度的匹配效果。

1 算法描述

文中算法流程如图1所示，步骤如下：

步骤1 对立体匹配图像对进行高斯下采样分解，得到不同尺寸的图像对，低分辨率分解层上对应的最大视差值也相应减小；

步骤2 在各个分解层上分别进行匹配代价计算和代价聚合，得到各个尺度下的匹配代价卷，提出将中心对称的Census变换与梯度信息相结合计算匹配代价，然后利用超像素分割进行快速初始聚合，再使用重启动与随机游走算法对其进行全局上的优化；

步骤3 对各个尺度分辨率下的匹配代价卷进行跨尺度融合，以实现匹配代价的有效融合更新；

步骤4 在最终的匹配代价卷上先采用引导滤波再次代价聚合，再使用WTA算法计算得出初始视差图；

步骤5 对初始视差图采用权重中值滤波对视差进行精细化，得到最终的视差图。

图1 本文算法流程图

1.1 计算匹配代价

传统Census变换是通过选取中心像素的灰度值作为参考，将其与窗口中各像素的灰度值进行比较，并用0和1表示大小关系。传统Census变换[17]的公式如下：

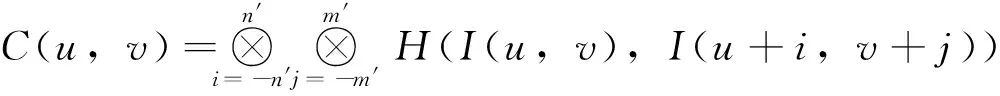
(1)

H(I(u，v)，I(u+i，v+j))=

(2)

传统Census变换能够在一定程度上降低噪声带来的干扰，但仍存在一定的局限性：变换结果完全依赖于中心点的灰度值，一旦中心像素点受到外界因素的干扰，Census编码结果会发生巨大变化，导致误匹配，降低匹配精度；其次，由于窗口内像素都要与中心像素进行比较再生成二进制码流形式，算法复杂度较高。故文中引入了中心对称的Census变换[18]，只有中心对称的像素点被比较，可以有效降低因外界干扰引起的变化，增强其抗噪声的鲁棒性；同时可以降低Census变换的计算复杂度。中心对称的Census变换[18]的公式如下：

Tl(u，v)=⊗H(I(u-i，y-j)，I(u+i，v+j))

(3)

Tr(u，v)=⊗H(I(u-i，y-j)，I(u+i，v+j))

(4)

其中，坐标(u-i，y-j)和(u+i，y+j)表示中心对称的坐标点，通过变换窗口可被转化为二值向量。

于是基于两个二值向量的汉明距离，可以得出参考图像和目标图像两个窗口之间的匹配代价：

Cr(u，v，d)=Ham(Tl(u，v)，Tr(u+d，v))

(5)

Cl(u，v，d)=Ham(Tl(u，v)，Tr(u-d，v))

(6)

式中，Cl(u，v，d)表示以左图作为参考图像，在像素点(u，v)、水平视差为d时的匹配代价；同理可知Cr(u，v，d)。

考虑到Census变换在重复和相似纹理区域可能会造成匹配模糊，为了解决这个问题，文中引入梯度信息来计算匹配代价，加强对图像边缘信息的获取，增强图像边界的鲁棒性。梯度图像匹配定义为

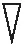
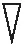
(7)

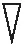
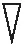
(8)

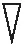
最后，通过融合中心对称的Census变换和梯度图像匹配可得最终的匹配代价：

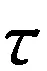
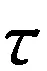
(9)

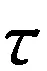
1.2 代价聚合

文中首先应用超像素分割算法进行代价聚合，一方面这种基于分割区域的聚合方法对噪声变化更具鲁棒性；另一方面，由于图像计算尺寸的减小，运算时间能够大幅降低，同时也减少了对硬件内存的需要。文中使用线性迭代聚类算法(SLIC)[16]进行超像素分割，其公式定义为

(10)

其中：ns表示属于超像素区域s中像素的数量；Fr(s，d)表示以右图像为参考图像的聚合匹配代价，同样对左图像进行计算Fl(s，d)。

之后再使用改进的重启动与随机游走算法对聚合结果进行全局优化。该方法不仅能减少计算量，而且避免了随机游走方法造成的视差图过度平滑和置信传播算法对于有环网络不能收敛到最优解的问题，可以达到理论上的最优值[1]。随机游走算法代价能量函数定义表示为

E(X)=μEdata(X)+Esmooth(X)

(11)

(12)

(13)

其中：式(12)中的xi和yi分别表示最终输出的匹配代价值和初始匹配代价值，对应于式(10)的Fr(s，d)；向量Edata(X)是向量X和向量Y之间的欧式距离的平方；wij是向量X的分量xi和向量Y的分量yi之间的连接权值；D是权值矩阵W的行元素组成的对角矩阵；N(i)属于平滑项的支撑区域；μ是Edata(X)和Esmooth(X)两者之间的调节项。

标准的重启动与随机游走全局最优化算法实现对E(X)的最优化求解得到最优解X，其求解过程可以转换为如下的迭代方程：

(14)

使用与边缘权重成比例的概率值将匹配成本传递到相邻节点，其中边缘权重受相邻超像素之间的亮度相似性的影响：

(15)

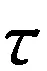
全局能量函数中平滑项易导致图像边界视差模糊，通过添加额外的保真项可有效改善上述问题。此外，通过添加可见项可有效提升遮挡区域的匹配性能：

(16)

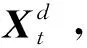
1.3 跨尺度融合

当前大部分立体匹配算法都是在图像原始分辨率尺寸上进行处理的，在高纹理区域能取得准确的视差值，但在低纹理或者重复纹理区域则效果不佳。考虑到人眼视觉系统是在不同尺度上处理接收到的视觉信号，并且对细节信息非常敏感。本研究借鉴文献[14]提出的多尺度聚合框架，实现匹配代价的有效融合，首先按照如下方式进行各尺度下匹配代价的融合更新：

(17)

(18)

由于式(18)所得融合后的匹配代价在各尺度之间是相互独立的，故在式(17)中加入二范数正则化项，以保证在多尺度下的一致性：

(19)

(20)

(21)

1.4 视差计算及求精

为了更有效突出图像边缘信息、增强纹理结构，对多尺度融合后的匹配代价卷采用引导滤波[4]进行再次代价聚合：

(22)

然后对其采用WTA(Winner- TakE-All)求解即可获得场景的视差图：

(23)

其中：d0∈{1，2，…，dmax}。

最后对所得视差图进行左右一致性检测，对错误像素和遮挡像素重新赋值，再进行权重中值滤波，这一方式可以在滤除噪声的同时，保护视差图的边缘信息不被模糊。

通过上述过程，可以有效提高视差图精度，降低误匹配率。

2 实验结果与分析

本文采用标准的Middlebury V3[20]立体匹配数据集来验证算法的有效性，利用MATLAB编程实现所提算法及相关对比算法。计算机配置为：Windows10，Inter(R)Core(TM)i5-7400，3.00 GHz主频CPU，8 GB内存。

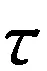
为验证文中所提算法的有效性，本研究选取了经典的引导滤波算法[4]、单尺度的ARW算法[13]、基于跨尺度的立体匹配算法[14]与文中所提算法进行实验对比。图2所示为上述各立体匹配算法所得视差图(截选Middlebury V3[20]立体匹配数据集中的Adirondack、Piano、Playtable、Teddy及其相应的标准视差图)；表1所示为相应算法于非遮挡区域(Non)以及所有区域(All)的误匹配率，误差阈值取1；图3为Adirondack图像视差匹配区域标记图，其中绿色区域表示遮挡区域误匹配，红色区域表示非遮挡区域误匹配。

表1 不同算法的误匹配率

Table 1 Mismatch rates of different algorithms

匹配图像误匹配率/%文献[4]算法文献[13]算法文献[14]算法 本文算法 非遮挡区域所有区域非遮挡区域所有区域非遮挡区域所有区域非遮挡区域所有区域Adirondack9.7511.8110.1316.1416.0421.546.6212.01ArtL15.9125.8222.6439.7213.7521.6813.9124.35Jadeplant31.8541.8627.1543.2928.6939.4523.2738.46Motorcycle11.7215.6011.4220.1910.2613.479.4217.18MotorcycleE12.8316.6511.6620.3411.4514.698.7317.15Piano18.1921.8917.8023.3415.9921.1815.3619.98PianoL37.9140.8536.3940.9036.4437.8135.5438.31Pipes12.8533.9415.9129.5515.7428.8712.7726.17Playroom22.6131.1322.6032.8626.4735.9218.1628.77Playtable46.0248.7119.0327.1214.8923.0114.5622.34PlaytableP14.4018.1615.2723.8415.2117.5213.0521.14Recycle10.8212.8013.9619.7411.2113.689.8211.50Shelves37.4338.4038.1141.6535.6938.9936.2537.51Teddy7.8413.378.5117.828.3416.827.0612.81Vintage39.6543.3329.7434.9531.5538.4523.6928.27加权平均误匹配率10.0425.0518.1927.4217.5423.6814.7322.23

由表1可以看出，文献[13]基于单尺度的ARW算法在所有区域的加权平均误匹配率为27.42%，而文中所提算法在所有区域的加权平均误匹配率为22.23%。相比之下文中所提算法加权平均误匹配率有所下降，表明采用多尺度融合的文中算法可以有效利用多尺度信息，从而提高立体匹配精度。文献[14]基于跨尺度的立体匹配算法在所有区域的加权平均误匹配率为23.68%，与文中算法相比匹配精度也较低。

由表1可知，对于Adirondack图像的立体匹配，相比于文献[13- 14]的算法，文中所提算法在非遮挡区域的误匹配率大幅度降低，误匹配率的降低在视差图上的表现为，文中所提算法得出的视差图整体轮廓更为清晰，图像噪点较少，且边界较为平滑。由图3可以看出，文中所提算法红色区域(非遮挡区域误匹配)与其他算法相比，明显误匹配区域更少。针对图2中的Playtable图像的重复纹理区域和低纹理区域(红色方框区域为具有低纹理的地毯区域，绿色方框区域代表的是低纹理和重复纹理交叉的白色椅子)，观察文中算法与其他算法在以上两个区域的视差图，可以看出文中算法可以很好地建模低纹理及重复纹理区域的对应关系。同时针对PianoL不同光照条件下的测试图像，由表1可知，文中算法相较于其他算法在光照条件不同时，误匹配率较低，证明文中算法对光照条件具有较好的鲁棒性。

表2为各算法的运行时间比较，文献[4]采用经典的引导滤波进行立体匹配，其运行时间最短；文中算法与基于单尺度的ARW算法[13]相比，需要在多个尺度上进行匹配代价和代价聚合，运行时间势必增加。

表2 不同算法的运行时间

(a)原始测试图像

(b)标准视差图

(c)文献[4]视差区域标记图

(d)文献[13]视差区域标记图

(e)文献[14]视差区域标记图

(f)本文算法视差区域标记图

针对Teddy图像的不同匹配代价方法视差图如图4所示，其中图4(b)为使用中心对称的Census变换，图4(c)为使用中心对称的Census变换和梯度信息相结合。对比图4(b)和图4(c)可以看出，在Teddy图像的左下角的遮挡区域，图4(c)算法效果更好，证明了有效结合梯度信息可以提高在遮挡区域的匹配精度。同时结合不同匹配代价方法的误匹配率结果(表3)可以看出，文中使用中心对称的Census变换和梯度信息相结合较单一匹配代价方法匹配精度更高，证明了文中算法结合方式的有效性。

综合上述实验结果及分析可知，文中所提算法与传统的引导滤波算法[4]相比，可以有效降低误匹配率，图像边缘信息更加突出；与单尺度的ARW算法[13]相比，文中算法在进行多尺度的融合后可以有效提升立体匹配的精度；与基于跨尺度的立体匹配算法[14]相比，文中所提算法在代价聚合阶段通过全局优化可以有效考虑到图像邻近像素之间的约束关系，减少误匹配点，能够提高整体的匹配精度，获得效果更好的视差图。同时由表4可以看出，与文献[7- 8]算法相比，文中算法匹配精度更高。

(a)标准视差图

(b)CS-CT

(c)CS-CT+Gradient

Fig.4 Teddy image of disparity map with different matching cost methods

表3 不同匹配代价方法的误匹配率

表4 文中算法与Middlebury部分算法的误匹配率的对比

Table 4 Mismatch rate comparision between the proposed algorithm and Middlebury algorithm

算法误匹配率/%非遮挡区域所有区域文献[7]算法19.126.2文献[8]算法17.024.6本文算法14.722.2

3 结论

在基于单尺度的重启动与随机游走立体匹配算法基础上，结合跨尺度代价聚合框架，提出了跨尺度的重启动与随机游走算法。该算法在代价聚合步骤中有效结合局部算法和全局算法的优点，先利用超像素分割实现代价聚合，再通过重启动与随机游走算法进行全局优化，最后通过跨尺度模型实现多尺度匹配代价的有效融合。在视差求精阶段，采用一系列优化方法(如引导滤波、左右一致性检测、中值滤波等)来提高最后视差图的精度。实验结果表明，文中所提算法可以有效提升立体匹配的精度。