基于分割树的视差图修复算法研究
2016-09-23郑豫楠
郑豫楠
(四川大学计算机学院,成都 610065)
基于分割树的视差图修复算法研究
郑豫楠
(四川大学计算机学院,成都610065)
0 引言
作为一项重要的研究领域,立体匹配在近十年有了明显的发展。许多新的算法被提出并且效果显著。Scharstein和Szeliski[1]提出了立体匹配算法的框架,并且将立体匹配算法分成了两种类型:局部算法和全局算法。局部算法(如经典的自适应权重算法[2])利用局部区域像素的颜色信息和梯度信息进行特征匹配,具有运算速度快、易于实现的优点,但缺点是在无纹理区域算法容易失效。全局算法利用全图的整体信息约束代价函数来计算视差,利用的全局优化算法有图割(graph cuts)[3]、置信度传播(belief propagation)[4]、动态规划[5]等,可以获得效果较好的视差图,但缺点是计算时间长,难以实现实时性。
局部立体匹配算法框架可以归纳为以下4个步骤:(1)初始代价计算;(2)代价聚合;(3)视差计算;(4)视差图修复。立体匹配研究发展至今,大部分的论文是关于第二步代价聚合的,但关于第四步视差图修复的论文并不多见。此外,通过局部立体匹配算法得到的视差图一般都会受到遮挡的影响,对于遮挡区域的像素难以估计出准确的视差值。
针对以上问题,本文提出了一种基于分割树的立体匹配修复算法。算法对象为局部立体匹配算法得到的视差图,先对输入视差图进行左右一致性检测将不一致的像素标记为不一致点,之后对视差图进行过分割处理,再利用高斯混合模型对每一个过分割区域进行视差值分配,最后利用过分割区域内像素视差一致性对不一致像素的视差值进行重新估计。
1 左右一致性检测
为了检测出受遮挡或其他因素影响导致的视差图中存在不准确的像素,算法的第一步是对输入的左右两张视差图进行一致性检测。对左视差图中的每一个像素,找到右视差图中对应位置的像素,比较两者视差差值的绝对值。如果差值绝对值在可接受的范围内,那么这个像素的视差值被认为是可靠的,反之,将其标记为不一致点。
在左右一致性检测结束后,根据(1)对被检测出的不一致点对代价聚合矩阵进行更新。

2 过分割视差图
颜色信息接近的区域,视差信息一般也较为接近,利用颜色信息对彩色图像进行分割,每一个分割区域内的像素的视差值会较为接近并且变化平滑。利用此先验知识,可以对检测出的不一致点的视差值进行修复,因此需要先对输入的视差图对应的彩色图像进行分割处理。
本文利用了 P.F.Felzenszwalb和 D.P.Huttenlocher[6]提出的方法进行分割处理,并且采取了过分割策略,即分割后的区域足够小,目的是使得上述先验尽可能成立。效果如图1。
在过分割处理结束后,会检测每一个分割区域内存在的不一致点的数量,如果不一致点的数量大于一定比例,会将这个区域标记为不可靠区域。
此外,还需要对每一个分割区域所对应的视差值和彩色值进行估计,以评估不同分割区域的相关性。本文采取的方法是通过高斯混合模型对视差图进行聚类处理,选取每一个区域属于同一个聚类数量最多的像素的视差值均值来作为其对应的视差信息,同时用每个区域所有像素彩色值的均值来作为其对应的颜色信息。
3 不可靠区域视差值估计

图1
不可靠区域的视差值信息并不可用,因此需要利用临近可靠区域的视差值对其进行估计。因此需要得到相邻分割区域的相关性,对每一个不可靠区域选取其相关性最大的临近区域的视差值作为它的视差值。
本文用Wi(Sp)表示分割区域Sp的第i个邻域对Sp的相关性:
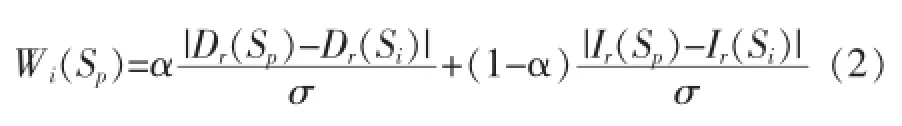
其中σ是预先设定的参数,用以归一化,Dr和Ir分别表示分割区域对应的视差值和彩色值,α表示Sp和Si的相邻程度:

其中Ni表示Si与Sp的公共区域长度,Nall表示Sp的周长。
因为不可靠区域的视差值存在一定不准确性,因此对每一个不可靠区域选取其相关性最高的可靠区域的视差值作为其新的视差值。
4 不一致像素的视差值估计
在得到不可靠区域的视差值之后,就可以对不可靠区域内部的不一致像素的视差值进行重新估计了。本文利用了一种先验,即在一个分割区域内部,所有像素的视差值均位于一个区间,即:
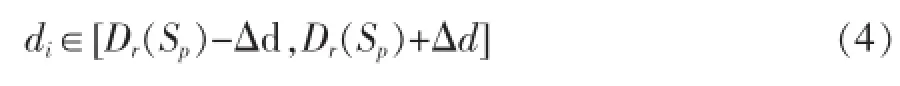
为了验证这种先验的正确性,可以使用真实视差图做实验。在本文所涉及的实验中,γ取值为5,R为255。结果表明99.2%的像素都符合这一先验假设,如图2。

图2 为真实视差图,红色标记的像素为不符合先验假设的像素
利用上述先验和更新后的不可靠区域的视差值,可以估计出每一个不可靠区域中的不一致点的视差值:

其中p表示不一致点,di∈[Dr(Sp)-Δd,Dr(Sp)+Δd],Cnew在左右一致性检测之后得到。每一个不一致点p的视差值都会使得新的代价聚合矩阵Cnew最小。
5 实验结果分析
本文的实验使用Middlebury[7]提供的图片和真是视差图进行评测,实验结果如图3所示。
在实验中,使用Mei X,Sun X,Dong W等人[8]提出的方法来获得初始视差图。结果表明本文的算法提升了一定效果,但部分区域和真实结果还有一些差距,仍有继续改善的空间。

图3
[1]D.Scharstein and R.Szeliski.A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms[J].IJCV,2002,47 (1-3):7-42.
[2]K.-J.Yoon and I.-S.Kweon.Adaptive Support-Weight Approach for Correspondence Search[J].PAMI,2006,28(4):650-656
[3]V.Kolmogorov and R.Zabih.Computing Visual Correspondence with Occlusions Via Graph Cuts[C].ICCV,2001:508-515.
[4]J.Sun,N.Zheng,and H.Shum.Stereo Matching Using Belief Propagation[M].ECCV,2002:510-524.
[5]郭永彩,魏朋玉,高潮.采用多级动态规划实现立体匹配[J].光学精密工程,2009,17(7):1745.
[6]P.F.Felzenszwalb and D.P.Huttenlocher.Efficient graphbased image segmentation[J].IJCV,2004,59(2):167-181.
[7]Middlebury Stereo Vision Page.http://vision.middlebury.edu/stereo/
[8]Mei X,Sun X,Dong W,et al.Segment-Tree Based Cost Aggregation for Stereo Matching[C].CVPR,2013:313-320.
Stereo Vision;Segment-Tree;Stereo Matching
Research on Disparity Map Refinement Algorithm Based on Segment Tree
ZHENG Yu-nan
(College of Computer Science,Sichuan University,Chengdu 610065)
1007-1423(2016)03-0068-04
10.3969/j.issn.1007-1423.2016.03.016
郑豫楠(1990-),男(汉族),天津人,硕士,研究方向为计算机视觉与图像处理
2015-12-08
2016-01-12
立体匹配是计算机视觉研究领域中的一项重要的研究问题。虽然已经存在很多立体匹配的相关方法,但是诸如遮挡之类的问题仍然没有被彻底解决。基于分割树的视差图修复方法,可以修复通过非全局性立体匹配算法得到的视差图。实验结果显示所提出的方法可减轻遮挡的影响。
立体视觉;分割树;立体匹配
四川省科技创新苗子工程(No.2015-095)
Stereo matching is an important problem in computer vision research field.Though many stereo matching methods have been proposed, but some problems such as occlusion are still unresolved.Proposes a method using segment-tree to refine a disparity map got from a nonglobal stereo matching algorithm.Experiment results shows that the proposed method alleviates the effect of occlusion.
