幼师数学教学中培养学生空间思维能力的研究

于萍

摘要：空间思维能力是一种普遍的思维能力，空间思维由三大要素组成：空间概念、呈现工具、推理过程。发展学生的空间思维能力，可以从理解空间意义，利用空间的各种性质形成问题，寻找答案，并呈现解决方案入手。幼师的立体几何教学，能培养学生的空间思维能力并为他们未来的幼儿园教学打好基础。当前，部分幼师学生的空间思维能力较低。通过引导学生观察、讨论、讲解、画图、制作几何教具、强化习题训练等形式，能全方位提升学生的空间思维能力。

关键词：幼师生;数学教学;空间思维能力

空间思维也称“多元思维”“全方位思维”“整体思维”，是指跳出点、线、面的限制，能从上、下、左、右，四面八方去思考问题的思维方式，也就是要“立起来思考”。空间思维能力不但对一个人的日常生活非常重要，也与其日后科学、技术、工程和数学领域的学习紧密联系。

幼儿教育是国民教育的基础，幼儿科学素养的形成与发展需要与之相匹配的教育。幼儿教师的空间思维能力直接影响到幼儿的空间思维能力的高低。数学教材中立体几何教学是培养学生空间思维能力的最有效途径。

教学中，我们要通过引导学生亲身经历、实际操作、语言表述、简单推理论证等方法来达到提升空间思维能力的目的。为此，我对学前教育专业“空间几何图形”教学内容进入了深度挖掘，结合幼师学生的特点，采取多种教学方式，注重激发学生的学习兴趣，让学生参与到课堂教学的各个环节;注重引导学生通过探究活动，得出问题的答案。通过观察、讨论、讲解、画图、制作几何教具等多种形式，全方位提升学生的空间思维能力。

一、强化概念教学，借助直观教具建立空间概念

基本概念是学生建立空间思维的基础，在教学中要加强基本概念的教学。教师要帮助学生理解空间概念的定义、定理、性质和一些推理的结论。幼师学生虽然学习过平面几何，具备了一定的图形知识，但其思维从二维平面图形向三维立体图形的转化仍有困难。要想使学生的空间思维方式顺利地完成由平面到立体的转化，教学中教师要依据学生的认知规律，由具体到抽象地设计教学过程。可以发给学生直观的教具，引导学生去观察、触摸、测量几何体。同时，引导学生通过直观教具的帮助，分清实物中线与线之间的关系、线与面的关系、面与面之间的关系。也可以引导学生自制学具，如准备一些牙签、橡皮泥和硬纸板等，把牙签当作直线，把硬纸板当作平面，用橡皮泥固定住牙签，做出研究问题中需要的各种几何体。在探究的过程中，能增强学生的信心、激发学习数学的兴趣、逐步建立空间概念，提升空间思维能力。

二、加强与实际生活的联系，感知空间观念

空间想象能力的基础是空间观念，而空间观念的来源是我们对现实世界的直接感知与认识。空间几何体是日常生活中很多物体的几何模型，教学中与日常生活相联系会增加几何体的直观性，降低抽象性。

教师可以充分利用教室这个立体空间，引导学生分析教室内的灯、墙面、黑板面之间的位置关系。还可以设置与生活相关的问题让学生探究，给予学生动手操作实践的机会。如在学习“长方体的对角线”时，我设置了如下问题：操场上有一堆砖，现在只有一把直尺，你能把其中一块砖的对角线的长度量出来吗？完成这道题，需要学生会找出长方体的对角线是哪条线段。在无法直接测量的情况下，要发挥空间想象力，借助“操场上有一堆砖”来达到解题的目的。（解这道题只需要把两块砖并排放在地面上，然后拿走其中的一块，刻画其在地面上留下痕迹，然后用直尺量就可以了）

在学习几何体平面展开图时，可以设置问题： 一个长方形的木块（如图1）， 已知AB=6cm，BC=5cm，BE=4cm。一只蜘蛛在长方体的顶点A处，一只蚊子在另一个顶点D处，问蜘蛛沿怎样的路线爬行，才能最快抓住蚊子？

解这道题，需要学生把几何体的平面展开图画出来，根据两点之间距离最短画线，计算连结A、D两点的最短线段的长度。

三、熟记画图规则，增强画图、识图的意识

画图和识图是学好立体几何的基础，也是教学的重点和难点。教师要重点研究在学习立体几何过程中学生的图形感知、识别障碍，帮助他们克服困难。

在几何体部分的教学中，需要学生掌握两种图形的画法，一是几何体的直观图，二是几何体的表面展开图。通过画直观图，可以把生活中的几何体在纸上直观地呈现出来。画直观图的目的是通过画图的训练，使学生达到在观看几何体的直观图时，能把几何体“立起来”，能看清几何体的点、线、面的各种关系。这也是培养学生空间思维能力的重要环节。 教学中，教师要帮助学生掌握画图规则，弄清画法原理，加大训练力度，增强作图意识。

通过画几何体的表面展开图的学习，学生可以掌握如何把一个几何体的各个面依次、连续地展开，并画在同一个平面内的方法。在学习过程中，学生对几何体的各个面之间的位置关系会有更深刻的认识，这有助于提升他们的空间想象力。同时，学生掌握了这种画图的方法，就可以根据需要，画出几何体的平面展开图，然后经折叠、粘贴，制成立体几何教具、学具。

四、设计趣味习题，提升空间思维能力

幼儿园中的数学活动带有趣味性，幼师学生也特别喜欢趣味性高的习题。每当做趣味数学题时，很多学生往往会忘掉对数学的恐惧心理，并积极地投入到探究之中。

在提高学生空间思维能力的数学活动中，经常会出现“折叠”“旋转形状”“切割”等主题。这些活动的设计和教学，需要较高的空间思维能力。很多学生的空間思维能力经过一段的学习，虽然得到了一定的提升，但是仍缺乏解决问题的变通和灵活性。为使他们在提升空间思维能力的同时，体会幼儿园数学科学活动的特点，在教学中我选取了最具有代表性、最简单的几何体——正方体来设计了四个问题。

通过一系列由浅入深的正方体趣味习题，使学生在平面图形与立体图形的转换训练中，快速提升了空间思维能力。

问题一：你能画出几个正方体的平面展开图？

学生画图，教师汇总，一共得出11种不同的画法。教师引导学生归纳这11种展开图的特点，总结规律，帮助记忆。目的是为后面探究正方体与其表面展开图的对应关系打下基础，提升学生画正方体表面展开图的能力。

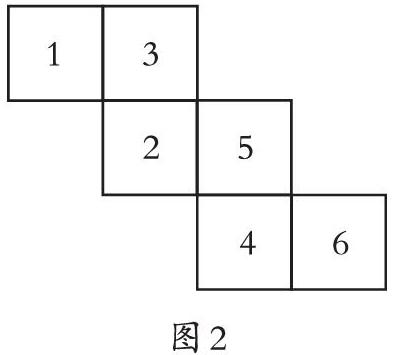
问题二：图2中给出了正方体的平面展开图，你能找出这个正方体中分别与数字“ 1 ”“2”“3”相对的面是哪些面吗？

学生通过探究，找出了与数字 “ 1 ”“2”“3”相对的面分别是数字“5”“6”“4”，然后教师要总结找相对面的规律和方法。通过这道题的训练，提升了学生把正方体的表面展开图抽象转化成正方体的能力。

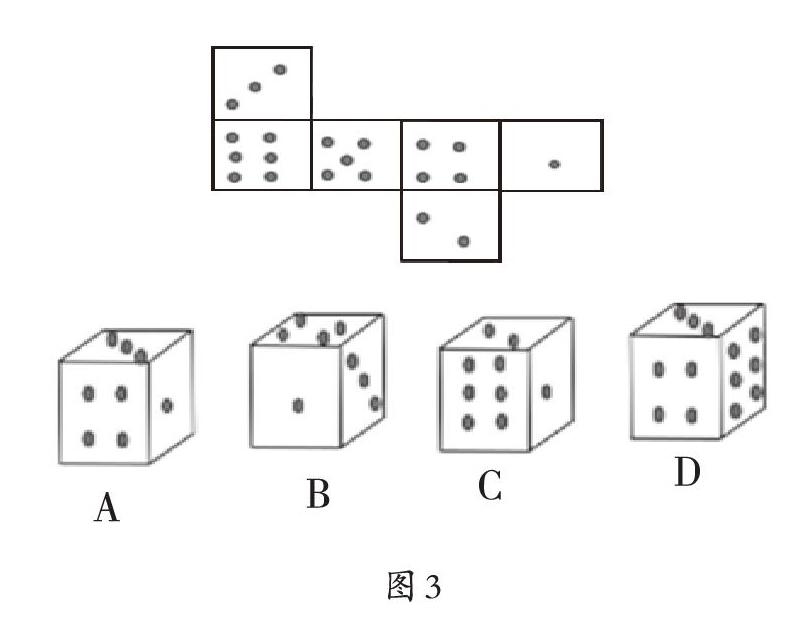
问题三：观察给定的正方体展开图，在下面四个选项中选出哪个几何体不能被它折出？（如图3）

这道题是在前两道题的基础上完成，需要较高的抽象思维能力。学生只有在头脑中經历一次把平面图形“立起来”的过程，利用找立方体相对面的方法、抽象思考每个面上“圆点”的摆放位置，才能给出问题的答案。在此过程中，学生空间想象力又得到一次提升。

问题四：把一个棱长为3厘米的正方体表面涂满红色，然后切成边长为1厘米的小正方体。请问：

（1）至少需要切几刀？

（2）最多能得到多少个边长为1cm的正方体？

（3）有多少个正方体三个面涂有红色？

（4）有多少个正方体二个面涂有红色？

（5）有多少个正方体一个面涂有红色？

（6）有多少个正方体六个面都没涂色？

这是一道立体图形空间切割题，需要更高的空间想象和抽象思维能力。可以鼓励学生合作探究，给出问题的答案。

通过这一系列习题的训练，学生不但掌握了立体几何的基本知识，还提升了逻辑思维能力、空间想象能力、画图能力、计算能力、分析问题和解决问题的能力，为幼儿园数学科学活动的创编打下了良好的基础。

五、制作几何玩、教具，适应幼教需要

“玩、教具设计与制作”是幼师学生必修的教育技能之一。幼儿园几何体的教学中需要大量的几何体教具和学具。在幼师立体几何教学中，教师应鼓励学生利用所学的几何体平面展开图知识制作学具、教具。学生掌握了这一技能，才能适应幼儿园教学的需要。

在学生制作教具之前，教师应教给学生掌握多种几何体表面展开图的画法，如柱体、锥体、台体以及五种正多面体的画法。实践中，可以让学生自由选取所要制作的种类。教师可以给学生展示上一届学生的优秀作品，使他们开阔眼界，打开思路，制作出更好的玩、教具。作品可以是一个几何体，也可以是一些不同的几何体组成的场景。为进一步提升学生的参与兴趣，我们还举行了全校的制作几何体教具大赛，学生参与的积极性很高。

参考文献：

[1]王祥.我们要学习“有用”的数学——浅谈立体几何主题活动教学对幼师生的影响[J]. 数学学习与研究，2014（3）.

[2]吴伟.高等幼儿师范学校立体几何教学的探索 [J].学园，2015（32）.

（责任编辑：杨强）