数形结合百般好,隔离分家万事休
2020-01-18吴进
吴进


摘 要:华罗庚先生说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离。”“数”的准确性和“形”的直观性,可以引导学生更全面地认识数学本质,发展学生的数学思维,触发高效的数学学习。
关键词:以形助数;以数解形;数形结合;小学数学
数学是一门研究客观世界中的数量关系和空间形式的学科,具有抽象性、逻辑性和概括性等特点,而“数”和“形”就是贯穿小学数学课本的两条基本主线。
■一、以形助数,抽象知识直观化
现阶段,在小学数学学习中,“数”指的是数与代数,包括了数的认识、数的运算、数量关系、常见的量等内容。然而基于学生数学核心素养的培养要求,我们传统的数与代数的教学就显得:重数量,轻质量;重过程,轻思维;重内容,轻生活;重形式,轻价值。
小学阶段,低年级学生的思维趋向于将数学知识与具体事物或生动表象联系在一起,高年级学生逐步学会区分概念中的本质与非本质属性、主要与次要的因素,学会用抽象、科学的定义概括生活表象,思维逻辑性逐渐增强。但是,总体而言,小学生的数学思维仍然趋向于将数学知识与直接的、感性的经验联系在一起,具有很明显的具体形象性。
因此,在小学阶段,如何赋予“数与代数”这块内容更多的趣味性、直观性、实用性,可以说是我们亟须考虑的问题!结合小学数学几何图形直观形象的特点,我们做了如下尝试。
1. 数的认识
数的认识,包含了自然数、整数、小数、分数等概念的学习,是小学数学学习中最基本的内容,是学生今后构建数的概念体系、掌握数的运算、探究数量关系的重要基础。那么如何建立起枯燥概念与直观图形的纽带呢?
我们就以认识“分数的意义”为例。分数的概念:把单位“1”平均分成若干份,取其中一份或几份的数叫作分数。如果单靠字面含义,难以理解分数的概念,而教材中直观图的及时呈现恰好可以提供帮助。例如,联系第2张图,学生明白了:把一个长方形看作单位“1”平均分成8份,取其中5份就表示“八分之五”。化抽象概念为具体事例的同时,加深了学生对分数的理解,为接下来学习分数的运算、数量关系的分析打下了坚实的基础。
2. 数的运算
数的运算指根据一定的数学概念、法则和定理,由一些已知量通过计算得出确定结果的过程。新课标指出,学生运算能力的培养要注重以下几点:理解运算意义,理解运算算理,掌握运算方法,选择运算方法解决问题。在传统的计算教学中,家长、学生、教师更注重掌握运算方法,鉴于其相对抽象、枯燥、死板,学生多采用“题海战”来强化练习,却对运算本质知之甚少。
为了发展学生的思维,探寻数学运算的本质,现阶段,帮助学生理解运算意义、理解运算算理才是我们计算教学的重中之重。那如何让枯燥的算理“活”起来,更易于学生理解呢?我们智慧的数学教师,契合小学生思维发展特点,想到了用图来化解难点。
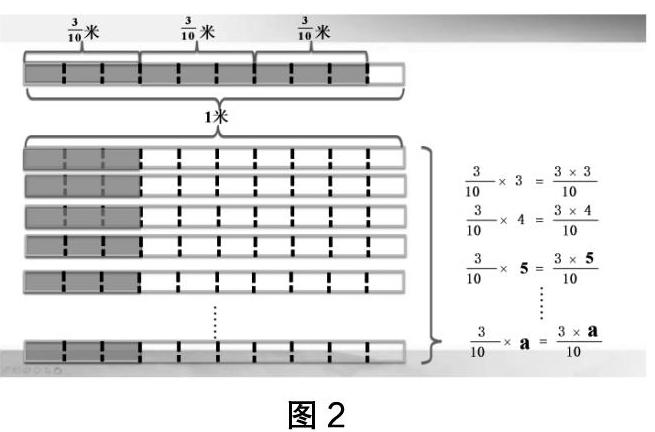
例如,在教学“整数乘分数”中,运算方法是:分母不变,分子与整数相乘的积作为分子。简单的一句话却包含了两个关键点:“为什么分母不变?”“分子与整数相乘的积表示什么?”多数学生对此是比较模糊的。而图形恰好可以形象地说明,其中一个小长方形表示一个“十分之一”米,分子乘分母就是计算有几个“十分之一”米。由图可见,“分母不变”是说明分数单位不变,“分子与整数相乘的积作为分子”表示有多少个这样的分数单位。从算理到算法,从一般到特殊,在帮助学生理解算理的同时,增强了运算学习的直观性、趣味性。
3. 数量关系
数量关系是从数学问题中总结出来的揭示某些数量之间的本质联系,并以数量关系式表示这种联系。因此,学生深刻理解、掌握“数学问题”背后的数量关系,对于解决同类问题,培养“举一反三”能力,形成对应的解题策略,发展数学思维,就显得尤为重要了。
为了在复杂问题中,清晰、准确地找到数量关系,我们小学数学中常用的方法之一就是“线段图”,它有助于將数学问题中数量以及数量之间的关系可视化、直观化。
例如,张宁和王晓星一共有78张邮票,张宁给了王晓星18张邮票后,两人一样多,那么张宁和王晓星原来各有多少张邮票?这个问题看似比较简单,然而“张宁给了王晓星18张邮票后,两人一样多”这句话很容易让学生误以为:张宁的邮票数-王晓星的邮票数=18(张)。但如果将条件和问题整理成一张线段图,学生可以轻易发现,实则:张宁的邮票数-王晓星的邮票数=36(张)。由此可见,线段图融合了条件和问题的同时,能够清晰地呈现数量之间的内在联系,其表现方式更契合小学生思维的形象性,更有助于学生数学思维的发展。
4. 常见的量
常见的量包括了时间、长度、面积、体积等知识。纵观小学阶段“常见的量”的学习,其抽象性让学生的体验感不强,大多数只会生搬硬套,不能够正确建模和应用。然而,抽象的文字却与生活实际紧紧联系在一起,我们数学教师的任务之一就是要架构起它们之间的桥梁。
例如,在教学“认识体积单位”时,常见的体积单位依次有立方厘米、立方分米、立方米,单靠文字,学生难以体验其实际大小。考虑小学生认知发展水平的直观形象性,以体验“1立方分米的大小”为例,一方面我们借助常见的几何图形进行理解:棱长是1分米的正方体,体积是1立方分米;另一方面我们借助生活中的物体进行理解:1立方分米相当于1个粉笔盒大小。多角度帮助学生化抽象为具体,让“冰冷”的知识“鲜活”起来,真正为学生的思想“减负”。
■二、以数解形,表面现象精准化
小学数学学习中,另一条主线是“形”,指的是图形与几何,主要包含四部分:图形的认识、图形的测量、图形与变换、图形与位置。纵观小学六年级中“图形与几何”知识板块的教学,“图形与几何”无论是在学习还是生活中,学生从直观、表面上去认识它们是比较容易的,但同时也是相对肤浅的。如果有了“数与代数”的支撑,我们就可以进一步深入、精准了解图形,挖掘图形的内在价值,为我们解决有关“图形与几何”的实际问题搭桥铺路。比如:
1. 图形的认识
以“认识长方体”为例。如果没有数据支撑,我们仅仅只是知道生活中的牙膏盒、油箱、游泳池等类似的几何形状是长方体;有了数据支撑,我们便知道长方体有8个顶点、12条棱和6个面,相对的棱长度相等,相对的面完全一样……从而我们可以依据长方体的特点,自主地制造我们需要的长方体物体。
2. 图形的测量
以“测量线段的长度”为例。如果没有数据支撑,我们仅仅只是知道上海去南京很远;有了数据支撑,我们知道两地大约相距300公里,开车大约需要4小时,坐高铁大约需要一个半小时,乘飞机大约需要1小时……可以帮助人们合理安排时间、合理安排交通出行。
3. 图形与变换
以“图形的放大與缩小”为例。如果没有数据支撑,我们仅仅只是知道照片可以放大或缩小;有了数据支撑,我们知道图形放大或缩小后,对应边成比例,形状才不会发生变化,可以按1∶2缩小,也可以按5∶1放大……依此,拍证件照片时,我们仅需拍一次照片,就可以按需要打印1寸、2寸等不同大小的照片。
4. 图形与位置
以“确定位置”为例。如果没有数据支撑,我们仅会用“四面八方”确定大概方向;有了数据支撑,我们可以知道具体位置在什么方向,多少角度,多少距离……例如,当军舰发现遇难船只在北偏东50°方向12海里处,可以更方便、更迅速地去展开救援。
由此可见,图形的直观性、简洁性确实在某种程度上契合了小学生的认知发展特点,但如果我们的数学学习仅限于此就难免显得浅薄了;而在数据支撑下,学生可以更深入、更细致、更精准地去了解图形、了解客观世界,体验数学学习的价值。
■三、数形结合,助推数学问题的有效解决
“数”表示抽象思维,“形”表示形象思维。“数形结合”告诉我们,使抽象思维与形象思维相结合,通过“数”与“形”的互相转化可以高效解决一系列数学问题。而从上面的交流中,我们也不难体会出“数学结合”思想对我们学习数学知识、解决数学问题、体会数学价值大有裨益。
小学阶段,学生的思维以具体形象为主,逐步向抽象逻辑思维过渡,小学生更多地能够体会到“以形助数,抽象知识直观化”的优点,若是能够巧妙地运用“数形结合”思想,往往会使抽象问题直观化,复杂问题简单化,达到优化解题路径,达到事半功倍的效果。而随着年龄的增长,学段的上升,尤其到了高中、大学阶段,学生会对“以数解形,表面现象精准化”的理解更加深刻。因此,我们高年级教学可以适当渗透,待学生以后进一步感悟。
