一种仿章鱼腕足柔性模块的设计与运动控制

，，，

(北京空间飞行器总体设计部空间智能机器人系统技术与应用北京市重点实验室，北京 100094)

0 引言

连续体机器人与具有刚性铰链的传统机器人不同，它主要由柔性材料制造而成，因此可以安全地与人进行互动，并适应各种非结构的复杂环境。

连续体机器人主要是由模块串联而成，所以模块的性能直接决定了连续体机器人的性能。目前模块驱动方式主要采用拉线和气动肌肉，美国Clemson大学的仿象鼻机器人[1-3]结构上分为4段，每一段采用四线驱动实现2个自由度运动。Walker与Jones的研究小组[4-6]还研制了一种仿章鱼腕足的连续体机器人OctArm。该机器人采用人工气动肌肉为驱动装置。人工气动肌肉由外部提供的压缩空气驱动，它可以提供很大的力量，而重量却比较小[7]。

模块采用传统驱动机构，驱动力大，有成熟的控制方案，但驱动机构体积大，推重比低，不利于机器人整体的轻量化和小型化。而采用SMA记忆合金，EAP等智能材料作为驱动器就可以克服传统驱动器的缺点，功率密度高，响应速度快[8-9]。

采用智能材料驱动器的模块形状检测较为困难。目前检测模块主要采用视觉、智能材料、压阻材料等方法。采用视觉测量有单目[10]和双目[11]，但环境适应性差，仅限于实验室。基于智能材料的检测上，主要有PVDF[12]和IPMC[13]材料，但仅限于一维运动测量。SMA合金弹簧作为一种智能材料，理论上可以通过测量SMA的电阻变化来控制SMA的拉伸和收缩，但SMA的电阻值不光与温度相关，还与载荷的变化相关，实际应用有较大的难度。针对上述问题，美国麻省理工学院提出了分段二进制控制方法[14]，但控制精度较差。

针对上述中驱动和控制方式出现的不足，在此提出使用SMA弹簧作为驱动器，利用线性霍尔传感器测量拉伸长度的变化实现对柔性模块闭环控制，并通过建立柔性模块的压缩数学模型提高对柔性模块弯曲角和旋转角控制精度。并组装柔性机械臂验证多节驱动器协调工作能力。

1 柔性模块结构

所设计的柔性模块如图1所示。

图1 柔性驱动器模块的结构示意

为让软胶的形状符合图1中的形状结构，用3D打印机打印出树脂材料的中心轴，再通过硅胶浇筑出中心轴的阴模，然后注入2种液体的混合物等待其硬化。中心轴上的凹槽为定位槽，用于定位环形支架，首尾的凹槽用于定位上下底座的位置。环形支架由3D打印机打印而成，支架周围的6个圆孔主要用于约束SMA弹簧的收缩拉伸运动，以及3个方向的SMA弹簧的相对位置。上下底座是用于固定SMA弹簧的基座，由于柔性模块还需要通过串联组成柔性机械臂，所以上下底座还设计有能相互连接固定的结构。由图1可以看出，上下底座都有环形沟槽，只需要连接上下底座，然后旋转就可以固定前后2段柔性模块。为了测量柔性模块的弯曲角和旋转角，模块上装有1组传感器。传感器由上下2部分构成，其中牵引支架通过拉线拉动3个方向上的磁钢上下运动，磁钢的运动被导轨限制，让磁钢和传感器之间只有竖直方向的位移，没有旋转运动。

2 柔性模块运动学建模

通常模块的运动学建模都是假设模块不发生轴向的压缩，但在实际上中心轴的硬度不高，轴向压缩是不可避免的。当模块弯曲时轴向也受力，模块会被压缩，导致3个方向的拉伸长度会随着弯曲角和压缩量共同作用而变化。所以拉伸长度变化和弯曲角变化的关系不具有唯一性。

在压缩状态建模，先考察柔性模块不可压缩状态。假设：柔性模块弯曲曲线为圆弧；柔性模块不可压缩。沿逆时针方向，方向1位于旋转角为0°的方向，方向2位于旋转角为120°的方向，方向3位于旋转角为240°的方向。如图2所示。

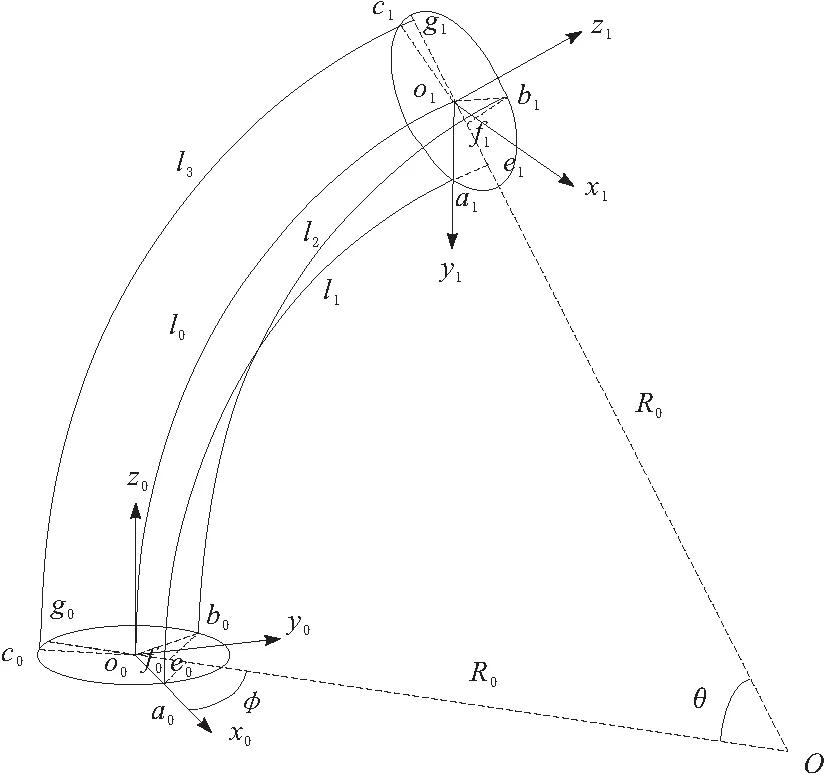
图2 柔性模块弯曲示意

l1为方向1拉伸长度；l2为方向2拉伸长度；l3为方向3的拉伸长度；r为3个方向上霍尔传感器与通过腕足中轴线的分度圆上的距离；θ为腕足弯曲角；φ为弯曲方向角。当弯曲角θ=0°时，l1=l2=l3=l0。当弯曲角θ=0°时，关节变量θ，φ和3个方向的长度变化量之间的关系为

(1)

两边同除以r可以得到

(2)

即弯曲角θ和旋转角φ分解成0°，120°和240°方向的弯曲角δj(j=1,2,3)。而Δlhj(j=1,2,3)和δj(j=1,2,3)的关系式为

(3)

由式(1)可以得到

Δl1+Δl2+Δl3=0

(4)

由式(4)可知：在不发生压缩的状态下，3个方向的拉伸和压缩距离相加等于零。

由于柔性模块各处曲率相同，所以通过测量柔性模块某一段的长度变化量可以反映出柔性模块整体的变化，由式(3)同理可得

Δlh1+Δlh2+Δlh3=0

(5)

而Δl和Δlh的关系式为

Δl=kΔlh

(6)

假设弯曲曲线为圆弧，考察霍尔传感器和磁钢的距离变化同时发生弯曲和压缩情况。如图3所示，初始状态3个方向的霍尔传感器和磁钢距离都为lh0。先做不可压缩弯曲变形，让弯曲角从0°变为θh，3个方向磁钢和霍尔传感器距离变化量为Δlhj(j=1,2,3)。然后让磁钢和霍尔传感器沿轴向发生压缩量为Δlhs的变化时，3个方向的实际距离变为lh1，lh2和lh3，弯曲角仍为θh。

图3 压缩状态示意

3个方向上距离变化关系式为

(7)

联立式(5)和式(7)可得

(8)

联立式(7)和式(8)可得

(9)

由式(8)可得到弯曲角相同时无压缩状态下3个方向的距离变化量Δlhj。在无压缩状态下排除压缩量的干扰。由式(3)和式(6)可知：Δlhj和δj具有一一对应的关系，Δlhj通过关系式δ=flδ(Δlh)求出δj。

3 柔性模块控制系统和原理

3.1 控制系统组成

上位机通过串行接口向单片机发送目标位置的电压信号。单片机通过AD口检测霍尔传感器的模拟电压信号，然后与目标电压信号比较，并通过PID运算向3个方向的加热驱动器发送PWM信号。加热驱动控制器控制加热SMA弹簧，使其相变收缩拉送柔性模块弯曲运动。控制系统和柔性模块连接如图4所示。

图4 控制系统示意

3.2 控制原理

控制框图如图5所示。

图5 系统控制框图

首先，上位机将柔性模块的目标弯曲角θ和旋转角φ转换成3个方向的目标弯曲角δj(j=1,2,3)控制器把当前3个方向数字电压信号Hj(j=1,2,3)发送给上位机。上位机将Hj转变为霍尔传感器和磁钢之间的距离lhj，通过式(9)算出无压缩的距离变化量Δlhj(j=1,2,3)。然后通过Δlhj和δj关系式求出3个方向当前的弯曲角。接着比较目标弯曲角和当前弯曲角的差值，改变给定目标数字电压信号H并发送给控制器。控制器将目标给定H与通过AD口接收电压信号Hj进行对比，通过PID产生PWM波控制加热控制器加热3个方向SMA弹簧，SMA弹簧受热发生相变收缩实现腕足弯曲和旋转到达相应的弯曲角θ和旋转角φ。

为了得到霍尔传感器和和磁钢距离Δlhj，首先必须通过实验来校正霍尔传感器建立起数字电压值Hhj和lhj关系式，以及Δlhj和δj的关系式，这样才能求出δj。

4 实验测量

4.1 霍尔传感器校正

考察霍尔传感器读数和距离变化之间的关系，通过霍尔传感器重新校正可得，如图6所示。

图6 数字电压读数和距离关系

当霍尔传感器和磁钢距离发生变化时，霍尔传感器输出电压随之变化，通过控制器的AD口(读取电压范围0～5 V，输出0～1 024)转变为数字电压信号。X轴为霍尔传感器和磁钢的距离lh；Y轴为数字电压信号H。用最小二乘法拟合可以求出lh和H的关系式为

lh=fHl(H)

(10)

4.2 弯曲角测量原理

视觉测量装置如图7所示。

图7 视觉测量装置

以方向1测量为例，让工业相机垂直于方向1的弯曲平面(旋转角为0°的平面)拍摄。在MATLAB中对拍摄图像进行处理测量得到弯曲角δ1，并同时记录下3个方向的霍尔传感器的数字电压信号Hj(j=1,2,3)，联立式(9)和式(10)计算出方向1在不可压缩状态下霍尔传感器部分距离的变化量Δlh1。

4.3 测量原理

假设腕足关节的弯曲为圆弧弯曲，向左弯曲为正向弯曲，向右弯曲为反向弯曲。实验目的是通过测量图像得到腕足的弯曲角。如图8和图9所示，首先要找到腕足关节中轴线的下端点O0和上端点O1。由于下端点O0为固定点，可以通过手动选取的方式找到，而上端点O1会随着腕足的弯曲，位置会发生变化，且上端点不便于放置追踪点。所以在腕足的上端部的两侧分别放置2个追踪点。让上端点O1位于这2个追踪点的几何中心点连线的中点上，而2个追踪点的几何中心可以通过计算机视觉追踪得到。

图8 腕足实物的图像

图9 测量原理

得到上端点O1后，利用圆弧的几何关系求出弯曲角δ1。连接O0和O1，求出向量O0O1和O0OR的夹角β，即腕足弯曲圆弧对应的弦长和水平线的夹角。ΔORO1O0为等腰三角形，所以弯曲角δ1=360-2β。通过测量得到的弯曲角δ1和上下端点，可以计算出腕足中轴线弯曲的理论弧线，用于对比腕足弯曲的实际弧线。

4.4 数据分析

让腕足往正反方向弯曲，进行10次弯曲。记录弯曲过程中霍尔数字信号H和对应的弯曲角θ。如图10所示。

由图10可知,由于向正反方向弯曲时，3个方向的SMA弹簧交替拉伸和收缩，腕足关节会发生不同程度的压缩。所以正反方向弯曲曲线不重合，霍尔数字信号和弯曲角的对应关系不具有唯一性。

再分析霍尔传感器和磁钢的无压缩状态拉伸距离Δlh和弯曲角δ1的关系,如图11所示。

图10 电压数字信号H1

和弯曲角δ1的关系 图11 无压缩Δlh和弯曲角δ1的关系

在无压缩状态下Δlh和弯曲角δ1应该是唯一对应关系，正反方向的曲线应该重合的。但由图11可以看出实际与理论分析结果并不相同。产生这种不重合的原因可能是：腕足在弯曲时并非理想状态的圆弧。

正反弯曲最大角度差3°，对于软体机器人来说，这种误差在可接受的范围内。把正反弯曲记录数据共同作为参考点拟合出方向1的平均关系曲线和关系式为

δ1=flδ(Δlh1)

(11)

同理3个方向的关系式可以表示为

(12)

5 柔性机械臂实验

柔性模块作为一个独立驱动单元，已经实现空间内运动轨迹跟踪。而柔性机械臂是由6节柔性模块串联而成，通过6节柔性模块的耦合运动后产生不同单节模块的运动形式。所以通过让柔性机械臂做出各种形式运动和抓取物体，来验证控制系统对柔性机械臂控制的有效性，以及柔性机械臂运动的灵活性。

5.1 柔性机械臂蜷缩

图12为柔性机械臂空气中平面运动实验结果。6节柔性机械臂垂直悬挂在支架上，每节初始弯曲角度为0°；图12a中设定第1节弯曲角为45°，实际误差不大，由于变形应力的传递，第2节和第3节有轻微弯曲；图12b中设定第1节和第2节弯曲角为60°；图12c中设定第1节和第2节弯曲角为60°，第3节弯曲角为-45°，第4节为0°，第5节为45°，第6节为0°，可以看出第4节能够保持末端弯曲角为0°但是整节发生S型变形，第6节在柔性机械臂自身重力作用下发生较大弯曲；图12d中调整第1节弯曲角为0°；图12e和图12f为整体的冷却恢复过程。

图12 柔性机械臂空气中平面运动

5.2 柔性机械臂水中运动

图13为柔性机械臂水面运动实验结果。

图13 柔性机械臂水面运动实验结果示意

图13中柔性机械臂从初始位置开始沿着预定运动轨迹，最后到达最终目标位置。初始状态柔性机械臂的第1节弯曲角为100°，第2节弯曲角为70°，第3节50°，第4节30°，第5节10°，第6节-10°。首先保持第6节角度不变，其他5节开始逐渐减少弯曲角，伸展到第6张图的状态，然后第1节和第2节开始反向弯曲运动，最后的运动依靠第6节，其他5节保持原有状态不变。第12张图重新处于蜷缩状态，并到达目标点。

6 结束语

设计一种由SMA弹簧驱动的柔性模块，通过霍尔传感器可以实时获取完全解读和弯曲方向。使用简单的PID和压缩数学模型，可以让柔性模块实现高精度的实时变形和二维运动。通过组合多节柔性驱动模块形成柔性机械臂。实验结果表明，此柔性机械臂可以根据预定目标轨迹进行运动，显示它相对于刚性机械臂有更大的运动灵活性。这种柔性机械臂为机器人的工程应用提供了更多亮点，例如在易碎物体，人工服务以及复杂障碍物环境中的移动。未来的工作将包括在执行更复杂的操纵任务时探索多段操纵器的性能，以及检测载荷的可行性。