基于Fluent的中间摆臂注射成型工艺参数优化

，，，，

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

金属粉末注射成形( MIM)是一种新型粉末冶金近净成形技术，它从塑料注射成形行业中引申而来。是将混合料(金属粉末与非金属粘结剂的混合物)作为原料，经过注射成形、烧结及后序加工工序，制取金属材料、复合材料以及各种类型制品的加工制造技术[1]。相比于传统工艺，MIM技术组织均匀，可制造结构复杂的产品，大大降低了生产成本。

但是MIM的工艺过程复杂，其中最关键的一道工序就是注射成型过程，注射成形参数直接影响到产品的开裂、分层、表面塌陷、欠注和内部缩孔等缺陷。在传统制造过程中往往采用经验公式和反复实验来消除缺陷，得到最优的注射工艺参数，这种方法不但成本高昂，而且无法将结果精确量化。随着有限元法、有限差分法等计算技术和计算机科学的进步，MIM的数值成型模拟研究在近年来受到了更多关注。通过充模过程的数值模拟，不仅可以动态地显示流体在模具型腔流动过程的温度、压力和速度的分布情况，还能预测可能产生缺陷的部位[2]。进而基于分析结果，对工艺参数进行优化，指导实际生产。在此，基于流体力学的基本控制方程，利用Fluent流体计算软件，对汽车发动机中间摆臂的充模过程进行数值模拟。

1 金属粉末注射成型多相流控制方程

考虑到MIM充模过程中，注射料通常为金属粉末和粘结剂的熔体，其一般被视作混合均匀的连续介质，是一种非稳态、非等温的非牛顿流体。在此，把金属粉末充模的过程看成是空气、金属粉末和粘结剂多相相互作用的过程。混合喂料中，粘结剂的体积分数占比相对更大，是混合料流动的主体，因此主要流体是熔融状的粘结剂，即为主相，第2相是金属粉末；除粘结剂和金属粉末两相之外，还需要考虑型腔内的空气的作用，它会随着喂料的流动而向型腔外部流动[3]，故而将空气视为第3相。根据流体力学理论，可建立以下方程。

a.质量守恒方程。

(1)

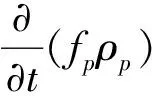
b.动量守恒方程。

(2)

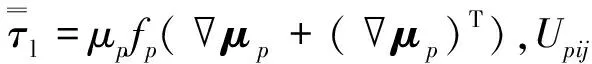
c.能量守恒方程。

(3)

等式的左边表示单位质量单元的能量与时间的比例关系；右边分别代表热传导，压力对单位质量流体所做的功、粘性耗散项和重力做功[4]。

2 中间摆臂模型建立和正交试验设计

2.1 几何模型及网格划分

模拟实验的对象是汽车发动机中间摆臂，其实物如图1所示。采用ICEM网格划分软件，对摆臂的3D模型进行区块化，生成非结构六面体网格，得到如图2所示的网格模型。对网格质量进行检查，六面体单元总数达到38 951个，节点总数达到25 310个。

图1 汽车中间摆臂注射成形坯 图2 汽车中间摆臂网格划分

2.2 喂料物性参数

在此，粘结剂主要由70%的石蜡、25%的聚乙烯和5%的硬脂酸组成；粉末注射成形喂料各组成成分的物性参数如表1所示[5]。

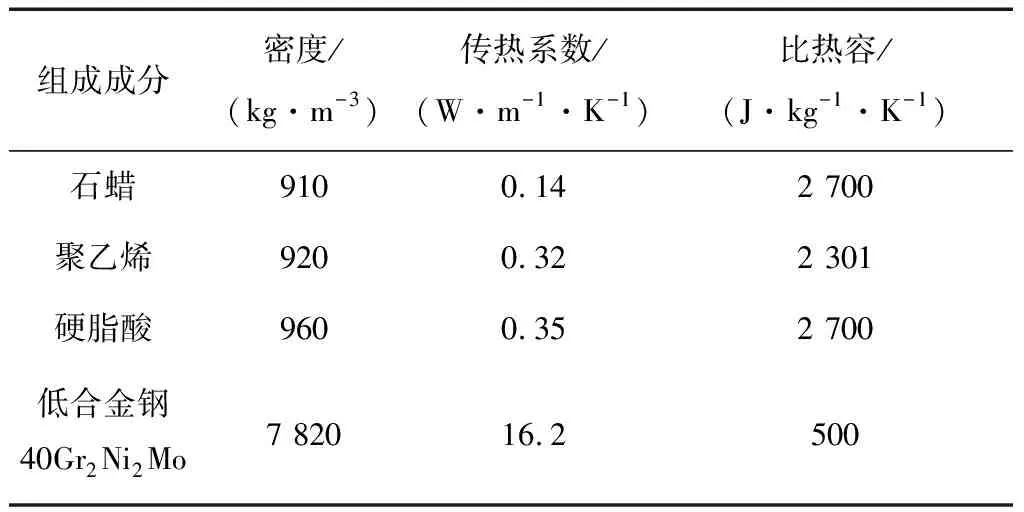
表1 喂料物性参数

根据各组元所占的比例，按体积分数加权计算得到：粘结剂密度ρb=915 kg·m-3;导热系数λ=0.195 5 W/(m·K);粘度n=0.45;比热容Cp=2 550.25 J/(kg·K)。

2.3 正交试验设计

试验因素水平如表2所示、表头设计如表3所示、正交实验因素安排如表4所示。

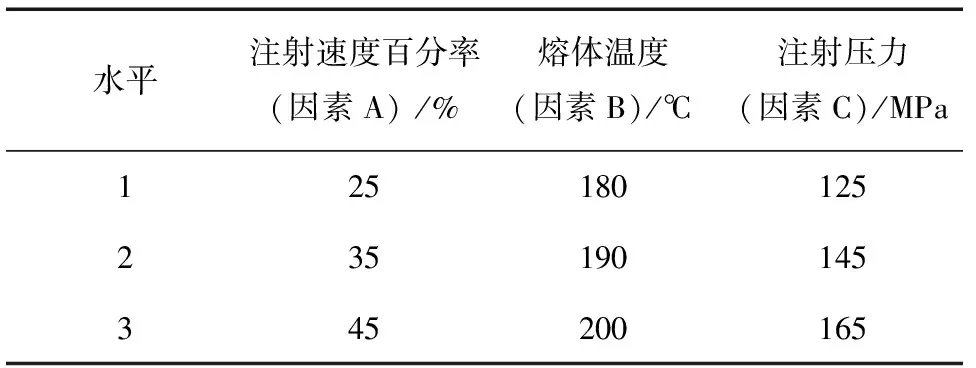
表2 实验因素、水平表

选择在注射成型过程中，充模阶段的射胶速度百分率(螺杆最大推进百分率)、熔体温度和注射压力作为研究对象。实验的目的是利用Fluent进行数值模拟，根据Fluent的分析结果，得到最佳工艺参数组合，对实际生产进行指导。实验以射胶速度百分率、熔体温度和注射压力作为3个因素A,B和C，每个因素根据注塑模具的相关经验公式选取3个水平，且同时研究各因子间的交互作用，故本文采用L27(313)正交表[6]。

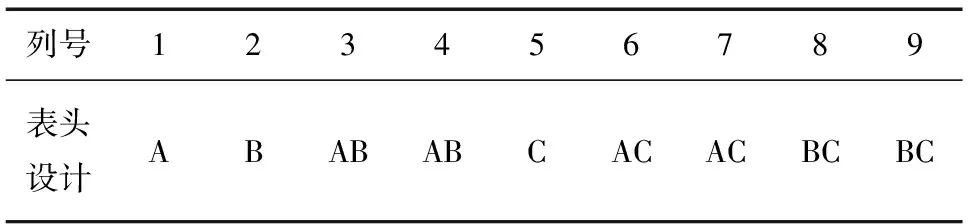
表3 实验表头

注：AB表示注射速度百分率和熔体温度之间的交互作用；AC与BC同理。

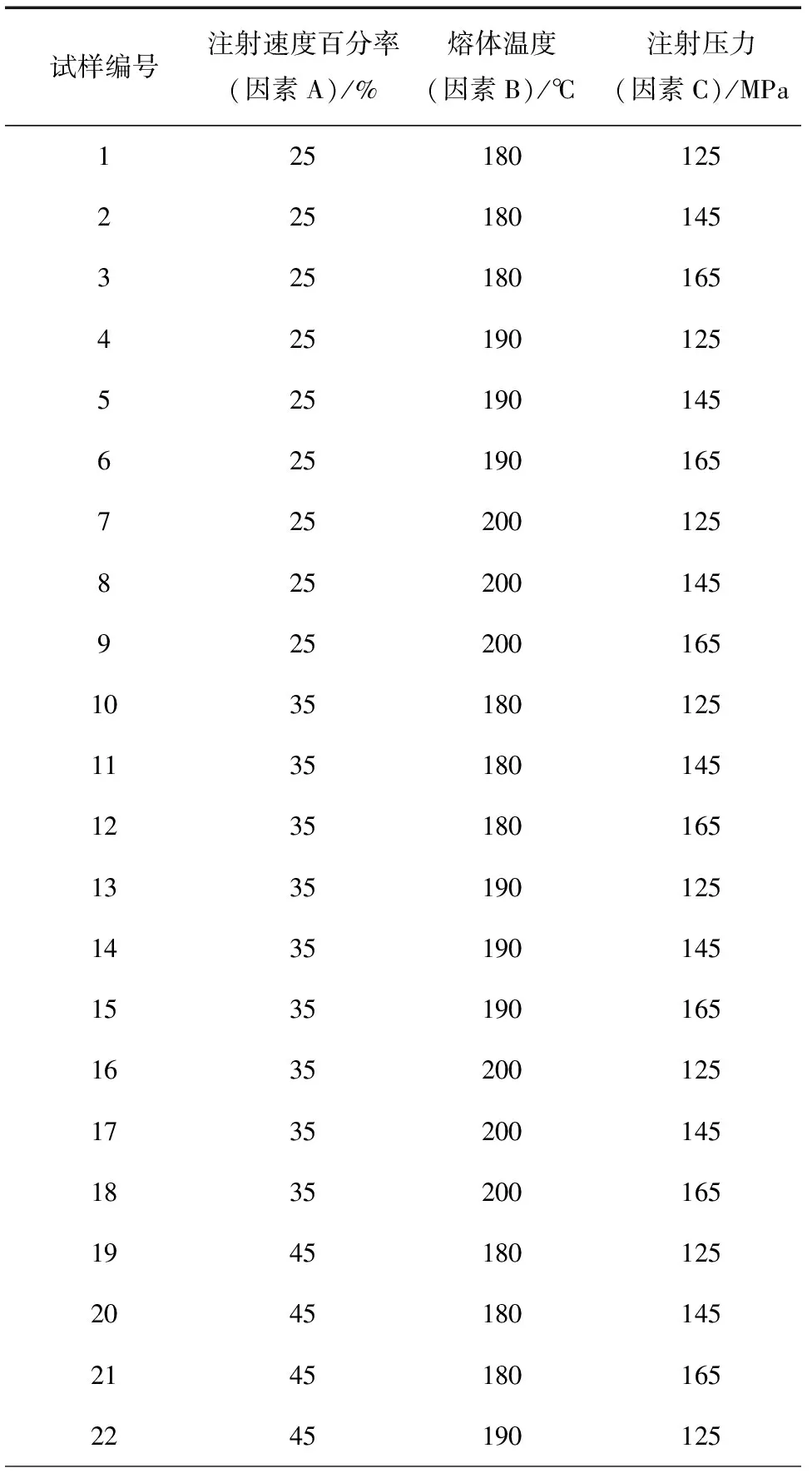
表4 正交实验因素安排表

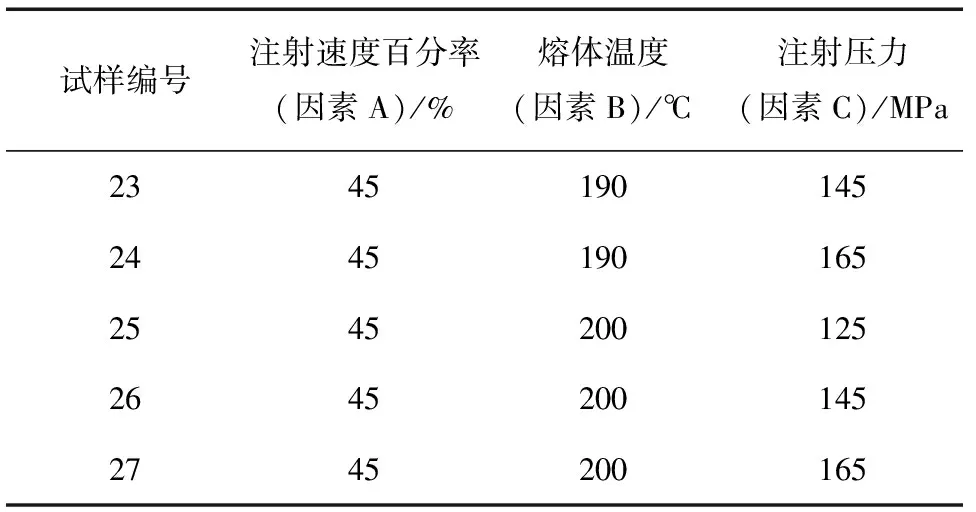
表4(续)

3 边界条件的设置

3.1 热传导边界条件

考虑到在设计注射模具时，模具具有冷却系统以保证型腔温度的稳定，故此处假设模具温度恒定为25 ℃，即流场外部温度恒定为25 ℃。已知边界对流换热系数α，根据热传导控制方程为

(4)

ρ，λ，Cp分别表示模具材料的密度、热传导系数和比热容；Q为热源相[7]。

3.2 运动边界条件

在入口边界上，速度边界条件根据注射速度计算公式为[8]

(5)

va为螺杆速度百分率(最大螺杆速度的百分率)为a时浇口的注射速度；l为加工该样件时，螺杆的射出行程；L为螺杆的最大射出行程；C为注射机注射量；S为浇口截面积。计算可得v45%=1.97 m/s，v35%=1.53 m/s，v25%=1.09 m/s。

压力边界条件：入口压力由注射机的实际注射压力确定；出口处未施加额外压力，故为标准大气压。

4 模拟结果分析

4.1 数值计算结果

根据Fluent模拟结果，可以直观地看到固相粉末的体积分数。下面主要分析在正交试验设定工艺参数条件下固相粉末体积分数的分布情况。同时结合实际生产，检查在各工艺参数条件下生产实验品的外观状况。

固相粉末的分布情况是影响成形坯料密度分布的重要因素，其直接决定制品的力学性能。表5为数值模拟仿真结果和各工艺参数条件下，制品的外观状况。

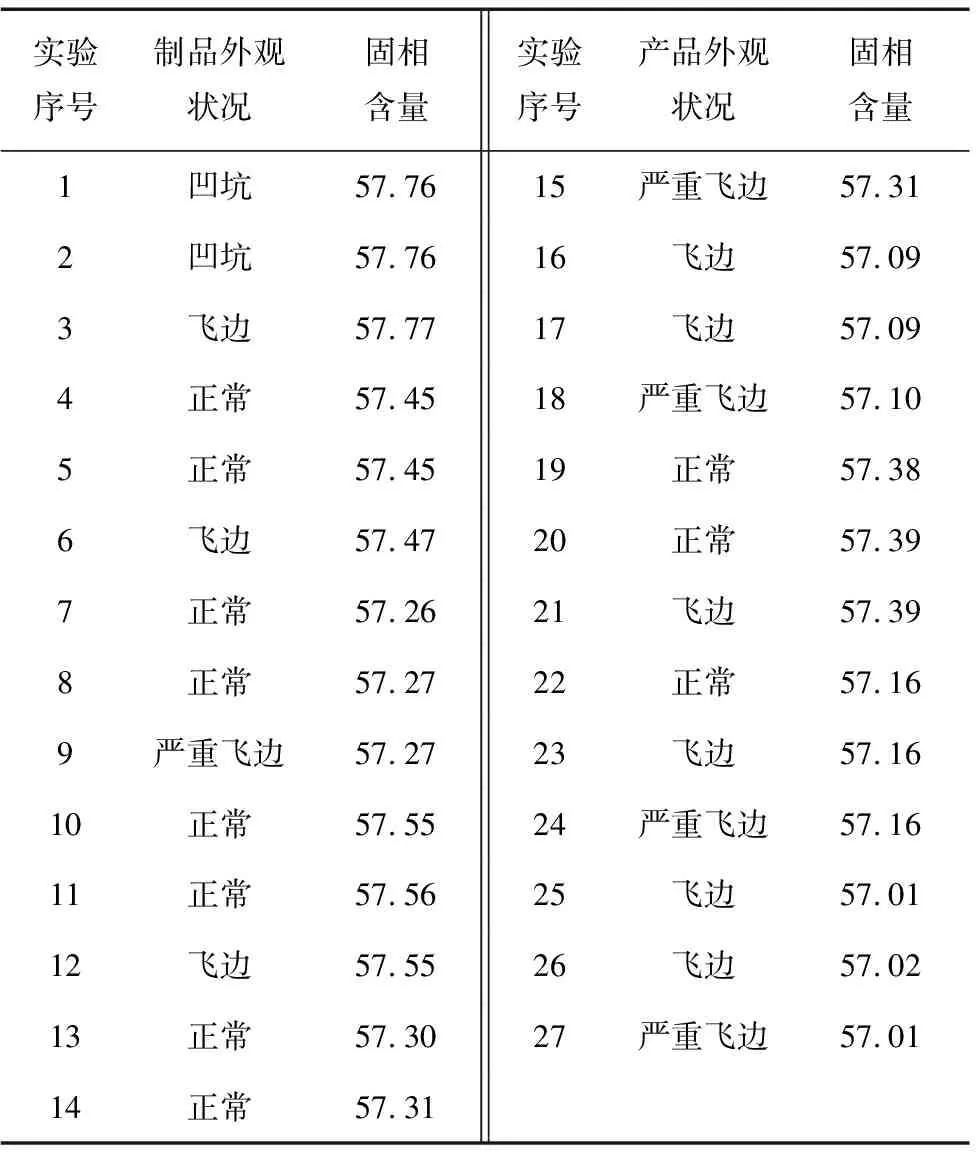
表5 实验结果 %

4.2 结果分析

由表5中制品的外观状况可知，第4、第5、第7、第8、第10、第11、第13、第14、第19、第20和第22组工艺参数组合能得到合格的制品外观，对比以上11组实验参数与其他缺陷组，可知：当注射压力和熔体温度分别与混合料的流动性成正比，制品容易出现飞边现象；当注射速度偏低，则制品容易在充模完成前冷却凝固，从而产生凹坑现象。

基于以上外观正常的11组试样，对其固相含量作极差分析。极差的大小与其对应因素对试验结果的影响程度成正比。直观分析结果如表6所示，表6中ki(i=1，2，3)是因素的各个水平的平均指标，按ki=∑di/m(m为包含水平i的实验次数,但未射出的实验排除在外)计算；di为水平i对应的固相含量；R为各项的极差(R=kmax-kmin)[9]。

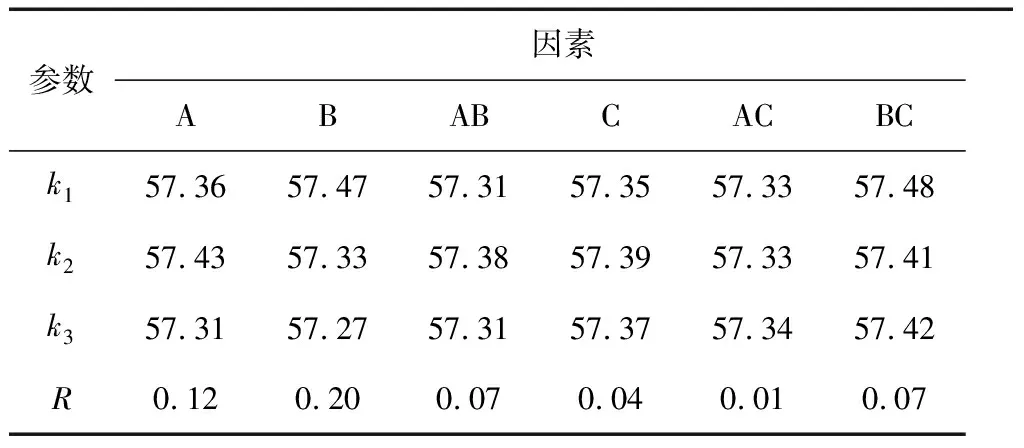
表6 实验结果-极差分析

对比表6中极差分析结果，可知各因子及其相互作用对固相含量W的影响大小：B>A>BC=AB>C>AC。Ai,Bi,Ci(i=l，2，3)表示各因素下，i水平时对应的实验条件(详情参照表2)。故优先选择因素A和因素B，对比因素A和B的3个水平数据，可知应选择A1B1，但该参数组合外观上存在缺陷，故因素A取A2，即A2B1。由于BC>C，所以分别对比B1C1,B1C2和B1C3结果，可知固相含量：WB1C3>WB1C2>WB1C1，虽然WB1C3最优，但其存在外观缺陷，且WB1C1低于WB1C2，故此取B1C2。因此A2B1C2为最优参数组合。此时注射速度百分率为35%，熔体温度为180 ℃，注射压力为145 MPa。

5 结束语

将金属粉末注射成形数值模拟技术和正交试验设计方法结合，作为优化粉末注射成形工艺参数的有效工具，从而避免单纯依靠经验公式得到工艺参数的盲目性与不可靠性。 对中间摆臂中固相合金粉末的体积分数进行了分析，并基于数值模拟结果，对各实验参数下，制品各部位固相的体积分数作了对比，得到最优工艺参数组合。 当工艺参数设置为注射速度百分率为35%、注射温度180 ℃、注射压力145 MPa时，得到的固相体积分数最高，达到57.56%。