关节铰接双面接触摩擦对医用机械臂影响分析

，

(兰州理工大学机电工程学院，甘肃 兰州 730050)

0 引言

医用机械臂是放射治疗系统中的主要组成部分之一，其作用是支撑患者进行摆位将靶区(肿瘤)置于束流照射范围内[1-2]。关节主要由电机、RV减速器、连接法兰等构成。其大臂、小臂的臂杆较长，重量较大且其运动平面与地面平行，因此在关节铰接圆柱面及端面都会出现摩擦，造成大量能量损失。文献[3]表明,机械臂关节上的驱动力矩(驱动力)大约有20%消耗在克服摩擦阻力上，关节摩擦不仅造成能量损耗还对机械臂的动力学特性产生影响。文献[4]表明关节摩擦的存在对机械臂速度及加速度的影响明显。文献[5]得出关节摩擦存在时，机器人低速的运动性能会恶化且对作业精确度影响较大。

在此，以医用机械臂为研究对象，基于库仑摩擦模型，利用拉格朗日方程分别建立不包含摩擦和包含关节铰接圆柱面及端面摩擦的动力学模型，并进行仿真分析这2处摩擦对关节输出扭矩及机械臂末端位置轨迹的影响。

1 不考虑摩擦时三杆医用机械臂动力学建模

医用机械臂三维模型如图1所示，对医用机械臂做如下假设：每个杆和关节都是刚性体；每个关节都只有1个转动的自由度。

图1 医用机械臂三维模型

由于拉格朗日法在分析多关节动力学特性上不涉及到约束力[6]，所以采用拉格朗日法来建立动力学模型。保守系统的拉格朗日方程形式为[7]

(1)

L=T-V

(2)

T为系统总的动能；V为系统总的势能。

将医用机械臂简化成如图2 所示的三杆结构，并建立固定坐标系OXY及参考坐标系O1X1Y1Z1,O2X2Y2Z2,O3X3Y3Z3，如图3所示。

图2 医用机械臂简化示意

各杆质心位置分别为m1,m2,m3;绕质心的转动惯量为IC1,IC2,IC3；LC1,LC2,LC3为各关节轴中心到相对应杆质心的距离；L1,L2,L3为各关节中心垂直距离。根据图3利用几何法求得各杆质心坐标位置矢量。

图3 医用机械臂坐标系

杆1质心坐标为

(3)

杆2质心坐标为

(4)

杆3质心坐标为

(5)

因为各杆绕定轴转动可以表示为质心的平移运动和绕质心的旋转运动2个运动的合成，所以系统总动能为

(6)

系统总势能为

(7)

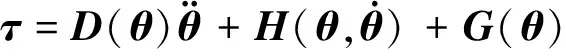
(8)

2 含摩擦的动力学建模

含摩擦的机械臂动力学模型基本形式为[8]

(9)

(10)

Tf1,Tf2,Tf3为各关节处总摩擦力矩，大小与所选的摩擦模型有关。本文选取库伦摩擦模型[9]为

(11)

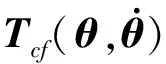
Tn=Fnr

(12)

Fn为法向接触力；r为作用半径。

2.1 法向接触力求解

首先将三杆医用机械臂各关节简化成如图4所示的接触形式，并将铰接圆柱面及端面描述成接触面1和接触面2。利用达朗伯定理对其进行动静力学分析，分别如图5和图6所示。

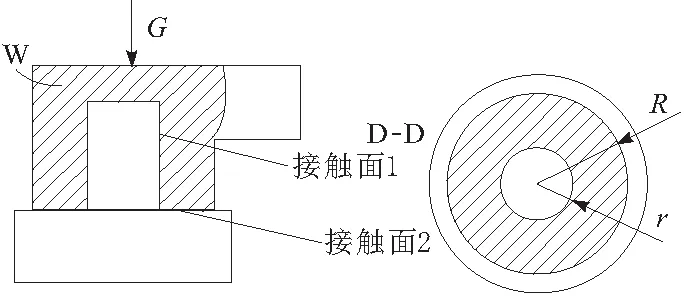
图4 铰接简化示意

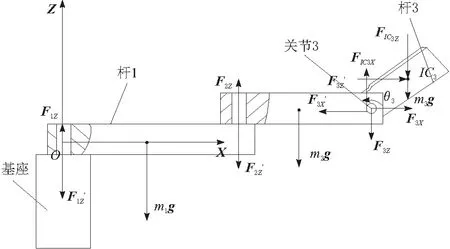
图5 B向医用机械臂受力分析

图6 A向医用机械臂受力分析

以杆1为研究对象：

(13)

以杆2为研究对象：

(14)

以杆3为研究对象：

(15)

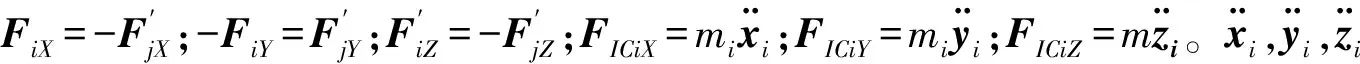
(16)

(17)

(18)

现定义接触系数α1和α2分别表示关节1和关节2的铰接接触面2的接触程度，其值与关节的结构、刚度、臂杆长度、装配精度等有关，且接触面2实际接触力与α1和α2成正比，则关节1和关节2铰接接触面2上接触力为

(19)

2.2 摩擦力矩求解

杆2与杆3之间相对运动速度较慢，所以忽略关节3处摩擦以简化问题的研究。库伦摩擦模型下关节1和关节2与接触面1上摩擦力引起摩擦力矩分别为：

(20)

(21)

u1,u2为关节1和关节2的两触面摩擦系数；r1和r2为作用半径;Tf′1X,Tf′1Y,Tf′2X,Tf′2Y为关节1和关节2在X轴、Y轴上的接触力作用下产生的摩擦力矩。接触面2摩擦力产生摩擦力矩为：

(22)

(23)

Tf″1为关节1与接触面2处的摩擦力矩；Tf″2为关节2与接触面2处的摩擦力矩；R1为关节1与接触面2的外径；R2为关节2与接触面2的外径；u3为关节1与接触面2的摩擦系数；u4为关节2与接触面2的摩擦系数。

库仑摩擦模型下各关节总摩擦力矩为

(24)

3 仿真分析

利用MATLAB对不含摩擦模型及含有库伦摩擦模型的动力学方程下的关节1和关节2输出扭矩进行仿真分析，表1为机械臂结构参数，表2为机械臂仿真运动参数。令R1=20 cm，R2=15 cm；r1=r2=10 cm。

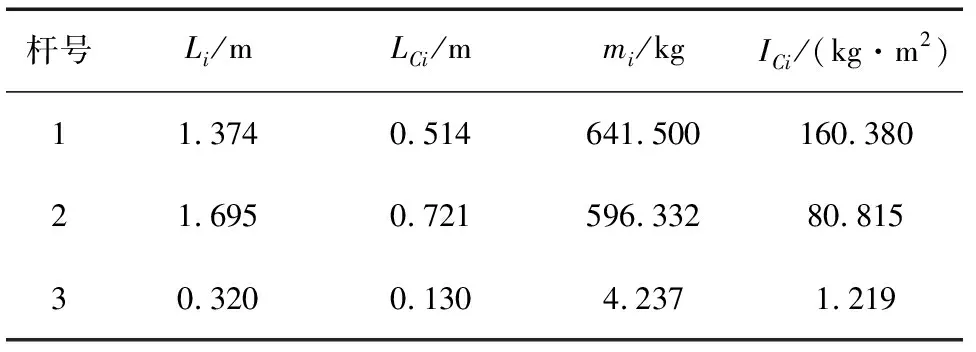
表1 医用机械臂主要参数

图7和图8为医用机械臂在表2的运动参数下，不考虑摩擦及分别考虑接触面1和接触面2摩

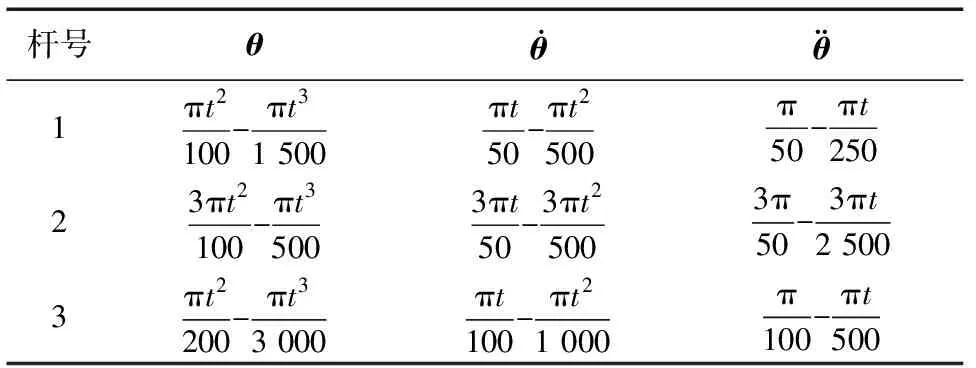
表2 医用机械臂运动参数

擦时，关节1和关节2在1～10 s的输出转矩。由图7和图8可以看出：在相同摩擦系数下， 当接触面系数α大于0.01时接触面2对关节输出扭矩的影响大于接触面1，随着α增大影响更加明显，而接触面1对输出扭矩的影响随着摩擦系数增大变化不明显，与现实情况比较相符。

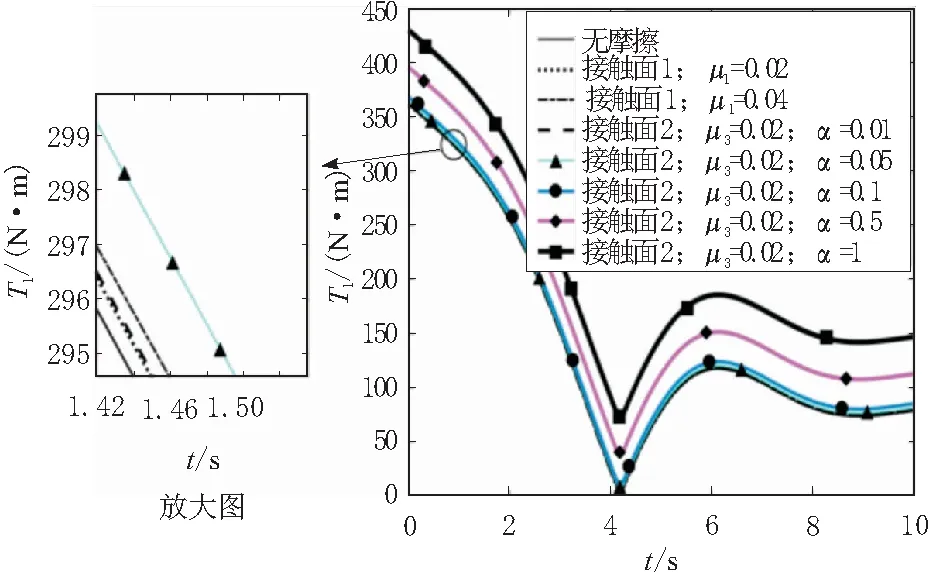
图7 关节1输出转矩

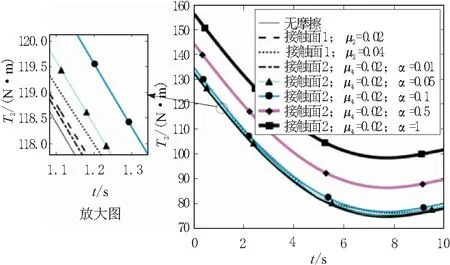
图8 关节2输出转矩

图9～图14为3个关节输出扭矩分别为T1=300 N·m，T2=200 N·m，T3=10 N·m下不考虑摩擦及不同摩擦状况下的末端位置仿真结果。图9和图10分别考虑关节1处接触面1和接触面2时机械臂末端轨迹，从图9～图10中看出，接触面1对机械臂末端轨迹影响远小于接触面2，随着接触面系数增大影响越来越明显，轨迹呈现不规则现象。图11～图14为考虑关节1的2个接触面摩擦分别与关节2的2个接触面摩擦耦合下的机械臂末端轨迹，可以看出当2个面都为接触面1时轨迹变化最小。

图9 关节1处接触面1摩擦时机械臂末端轨迹

图10 关节1处接触面2摩擦时机械臂末端轨迹

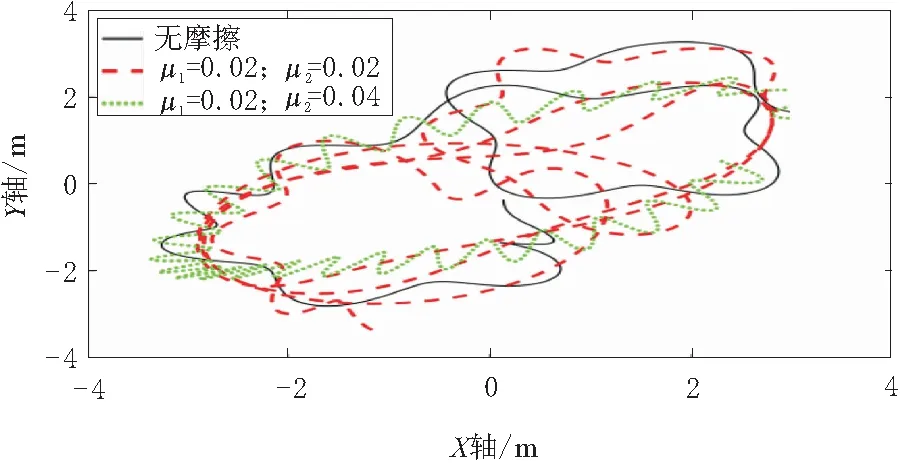
图11 关节1、关节2处接触面1摩擦时机械臂末端轨迹

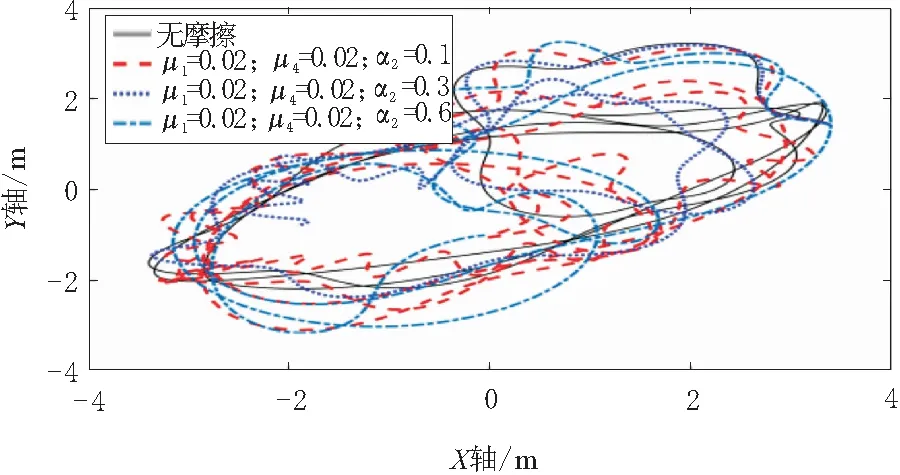
图12 关节1处接触面1及关节2接触面2摩擦时机械臂末端轨迹

图13 关节1处与接触面2及关节2接触面1摩擦时机械臂末端轨迹

图14 关节1、关节2处接与触面2摩擦时机械臂末端轨迹

4 结束语

以医用机械臂为研究对象，基于拉格朗日方程并利用达朗伯定理建立了不包含摩擦及包含摩擦的2种动力学模型，同时引入接触面系数α1和α2。通过仿真分析得出当关节铰接的2个接触面摩擦系数相同时，铰接端面(接触面2)的接触面系数超过一定范围时对关节输出扭矩影响明显大于铰接圆柱面(接触面1)影响，同时也会造成巨大的能量损失，因此在设计制造过程中可以通过提高关节刚度，减小杆的长度，提高装配精度等方法减小关节铰接端面的接触程度。通过对机械臂末端轨迹仿真分析可知：铰接端面对机械臂末端轨迹影响明显大于铰接圆柱面，因此在精度要求较高的情况下，对于与本文的医用机械臂及结构相类似的机械臂，对其建模时应该着重分析关节铰接端面的接触程度且不可以忽略，以免造成巨大的能量损失及误差。