双梁门式起重机静动态特性分析
2020-01-10□彭军
□彭 军
一、引言
作为一种常见的起重运输机械,门式起重机(以下简称门机)具有场地利用率高、作业范围大、通用性强等优点,广泛应用于铁路及港口货场等生产区域。门机工作时,主要承受由起重小车起吊货物引起的垂向载荷,起升、运行及制动机构的启停引发的冲击载荷等,另外,由于货物的摆动等原因,整机结构会承受来自各个方向的随机振动,当外界振动载荷的频率与结构的固有频率接近时就会引发共振,造成结构更大的破坏。因此,在进行门机设计时非常有必要深入研究其静动态特性。邹湘等人[1]以某造船用门式起重机为研究对象,利用ANSYS Workbench对结构的刚度和模态进行了分析。刘磊[2]为了研究某单梁门式起重机的动态特性,利用有限元软件对其开展了模态分析和瞬态动力学分析。马世辉等人[3]则通过模态分析和谐响应分析来研究某桁架门式起重机的动态特性,获取了结构的固有频率、振型及易产生共振的频率。文广等人[4]和谭云波等人[5]均从静动态特性分析的角度分别对桁架式门式起重机展开了研究,研究结果为门机结构的优化改进奠定了基础。刘岳嵩等人[6]在研究某锌合金门式起重机动态特性时发现,当起重小车位于主梁跨中和悬臂端时整机模态振型表现一致。韩伟等人[7]以某带蒙皮的门机金属结构为分析对象,利用ANSYS软件对其模态特性和瞬态动力响应进行了分析,计算结果为起重机蒙皮的设计提供了理论依据。江爱华等人[8]从仿真和试验的的角度对某门式起重机金属结构的载荷响应进行了研究。本文以有限元软件ANSYS作为计算工具,对某双梁门式起重机金属结构的静、动态特性进行分析,获取其静强度、静刚度、固有频率及振型等指标参数,分析计算结果为接下来开展该门机金属结构的优化设计奠定了理论基础。
二、双梁门式起重机金属结构数值模型
该门机金属结构如图1所示。整机金属结构均由Q235B材料制成,该材料的密度是7.85×10-6kg/mm3,材料的泊松比是0.3,材料的弹性模量是2.1×105MPa,材料的屈服强度是235MPa,按照起重机设计规范GB3811-2008[9]的相关规定,校核起重机金属结构的强度时,应定义相应的安全系数,本文取1.34,通过计算得到该材料的许用应力为175MPa。
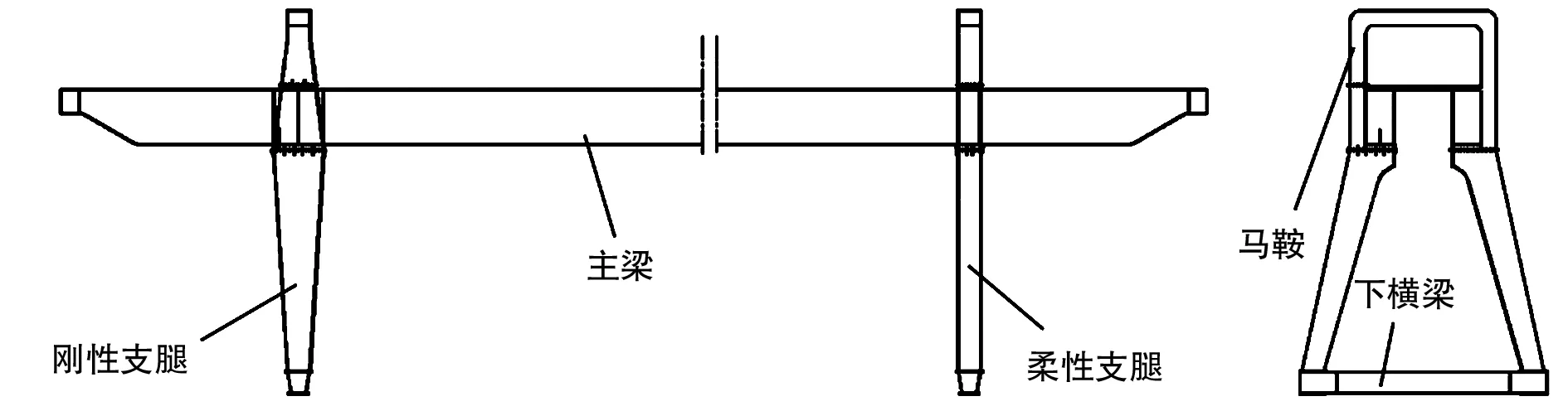
图1 门机结构简图
分析时,建立该门机金属结构的数值模型,选择在有限元软件ANSYS中实现。为了在保证计算精度的前提下尽量提高建模、分析计算的效率,按照结构有限元分析的建模原则忽略了起重机上的栏杆、电缆、轨道等附属结构件。实体模型建立后,整机金属结构使用shell181单元来模拟,网格划分的方式则选用映射方式,网格划分后,整机模型被离散为6,812个单元,节点的个数则为6,642。图2给出了离散后的门机金属结构数值模型。

图2 门机金属结构有限元模型
三、门式起重机金属结构静态特性计算结果
在建立该门机金属结构数值模型基础上,按照该门机金属结构的实际工作条件定义其约束和载荷。考虑到大车运行轨道对起重机大车车轮的支撑作用,在该门机支腿与轨道接触处,对整机金属结构有限元模型施加相应的位移约束,具体的约束条件如下:在左端刚性支腿前部支承处,约束其沿小车轨道方向、竖直方向、大车轨道方向上的平动自由度,在左端刚性支腿后部支承处,约束其沿小车轨道方向、竖直方向上的平动自由度;在右端柔性支腿前部支承处,约束其沿大车轨道方向、竖直方向上的平动自由度,允许其沿小车轨道方向存在10mm的位移,在右端柔性支腿后部支承处,约束其沿竖直方向上的平动自由度,允许其沿小车轨道方向存在10mm的位移。主梁在工作时主要承受来自起重小车起吊货物引起的垂向载荷,并且,起重小车会沿着主梁上方的轨道移动,为了全面分析该门机在工作载荷作用下的静态特性,考虑起重小车分别位于主梁跨中、左右悬臂端等位置时的三种典型工况进行计算。该门机的额定起重量为20t,起重小车的质量为18.5t,计算时,考虑起重机的起升动载效应,将额定起重量和起重小车的重量相加并乘以起升动载系数后加载到主梁指定位置。通过计算得出该双梁门式起重机金属结构在指定工况下的等效应力及位移云图(如图3、图4所示)。
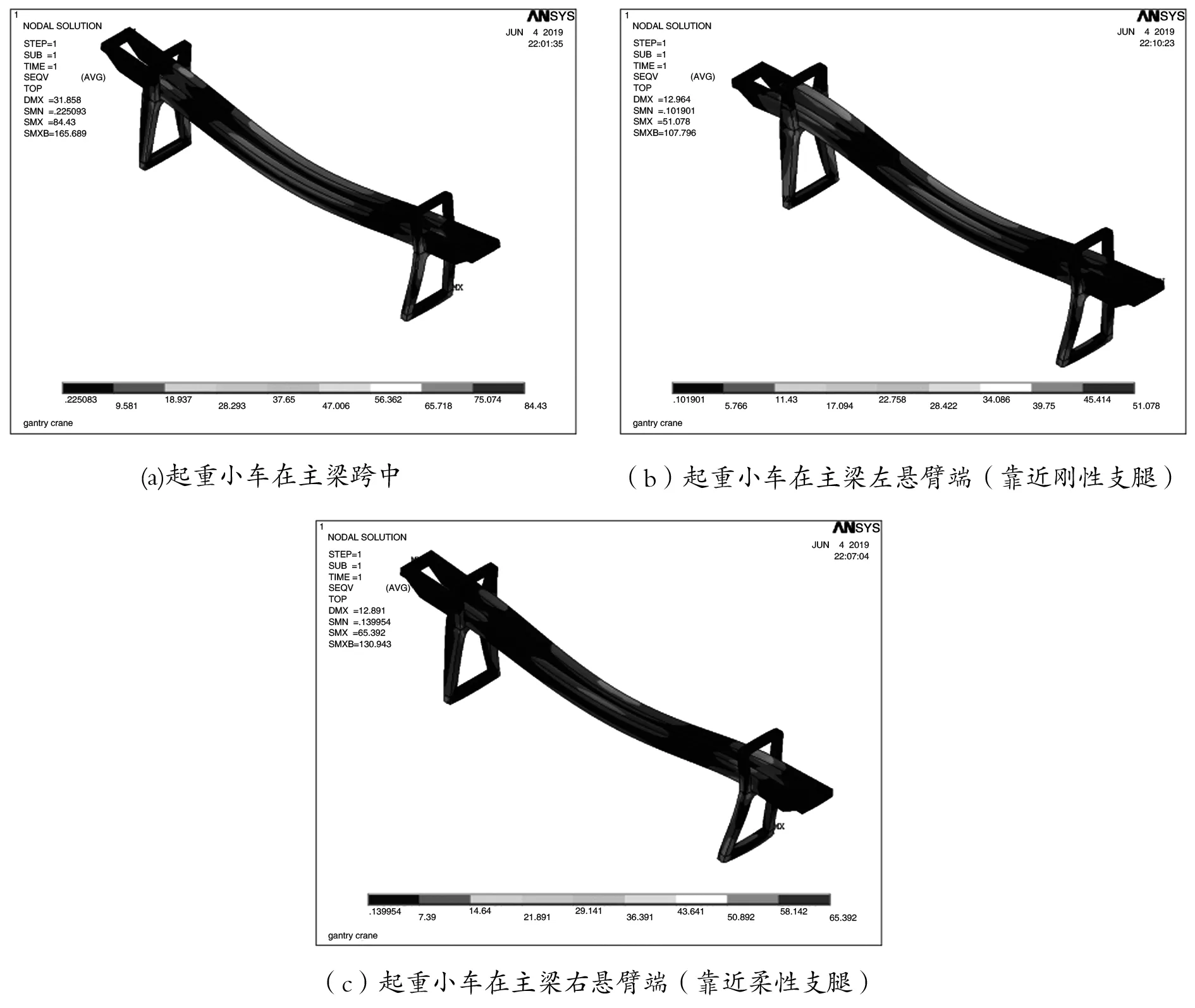
图3 门机主梁工作应力云图
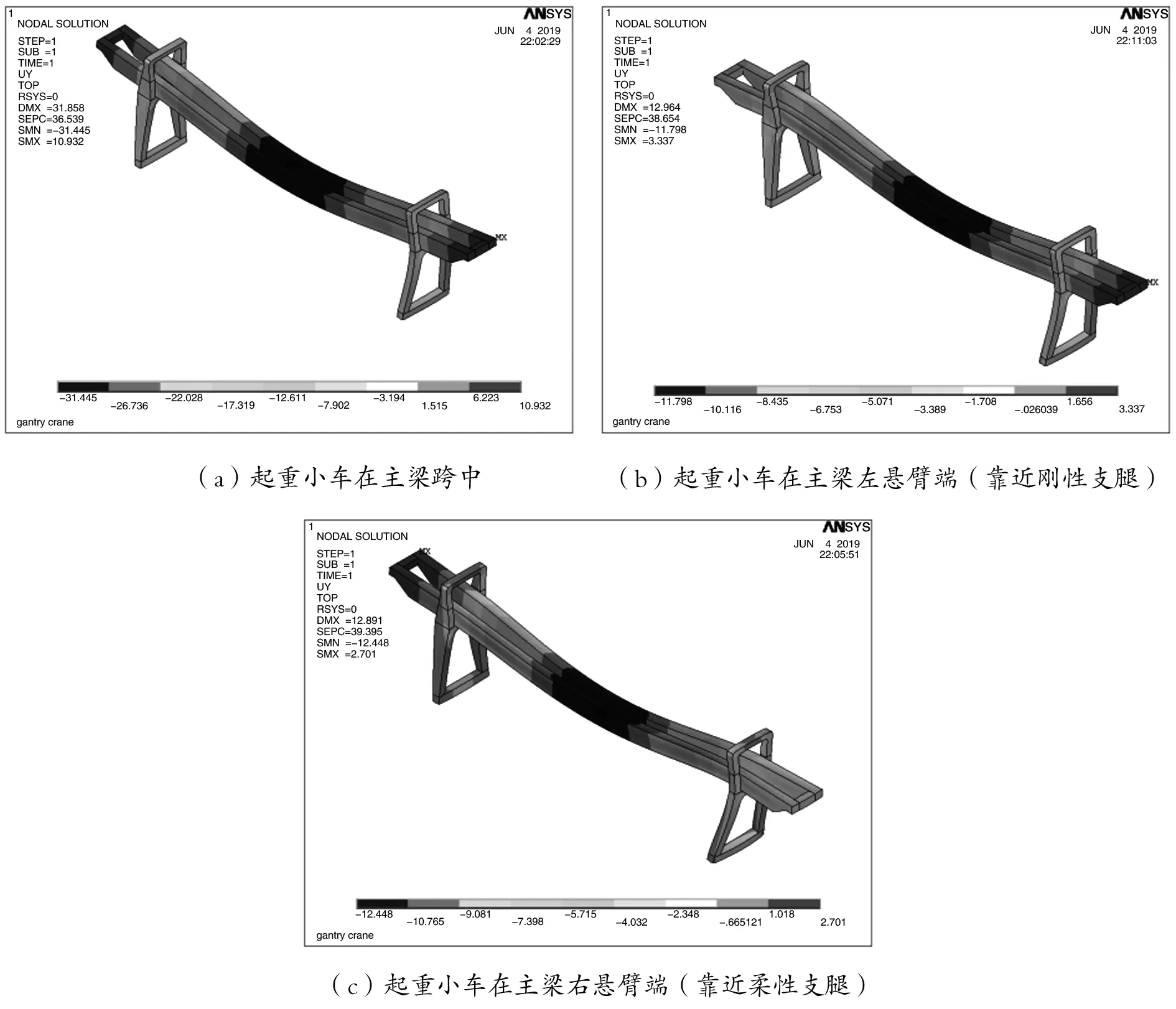
图4 门机金属结构竖直方向位移变形云图
从图3(a)可以看出,当起重小车位于主梁跨中时,最大应力发生在柔性支腿与下横梁交接处,最大应力值约为84.43MPa,其值远小于材料的许用应力值;从图3(b)可以看出,当起重小车位于主梁左悬臂端时,结构最大工作应力发生在刚性支腿与下横梁交接处,其值为51.078MPa,从图3(c)可以看出,当起重小车位于主梁右悬臂端时,结构最大工作应力发生在柔性支腿与下横梁交接处,其值为65.392MPa。
从图4可以看出,在三种计算工况下,整机结构在竖直方向上的最大位移变形均发生在主梁跨中,其中,当起重小车位于主梁跨中时,其位移变形最大,变形值达到了31.445mm。
四、门式起重机金属结构模态计算结果
模态分析和谐响应分析是基于有限元法的结构动力学分析中比较常见的类型,其中,对结构开展模态分析[10]主要是为了求解结构的振型和固有频率等动态特性参数,对结构开展谐响应分析则是为了考察外界激励载荷作用下结构的动态响应。
为了获取该门机金属结构的固有频率和模态振型,利用兰斯索斯法[11],对该门机金属结构进行模态分析。分析时需要定义模态提取及扩展阶数,相对而言,结构动态特性对低阶模态较为敏感,为了提高分析效率,本文只提取了该门机金属结构的前6阶模态。该双梁门式起重机金属结构的前6阶固有频率值如表1所示,图5给出了该结构的前6阶振型。

表1 门机金属结构模态固有频率 单位:Hz
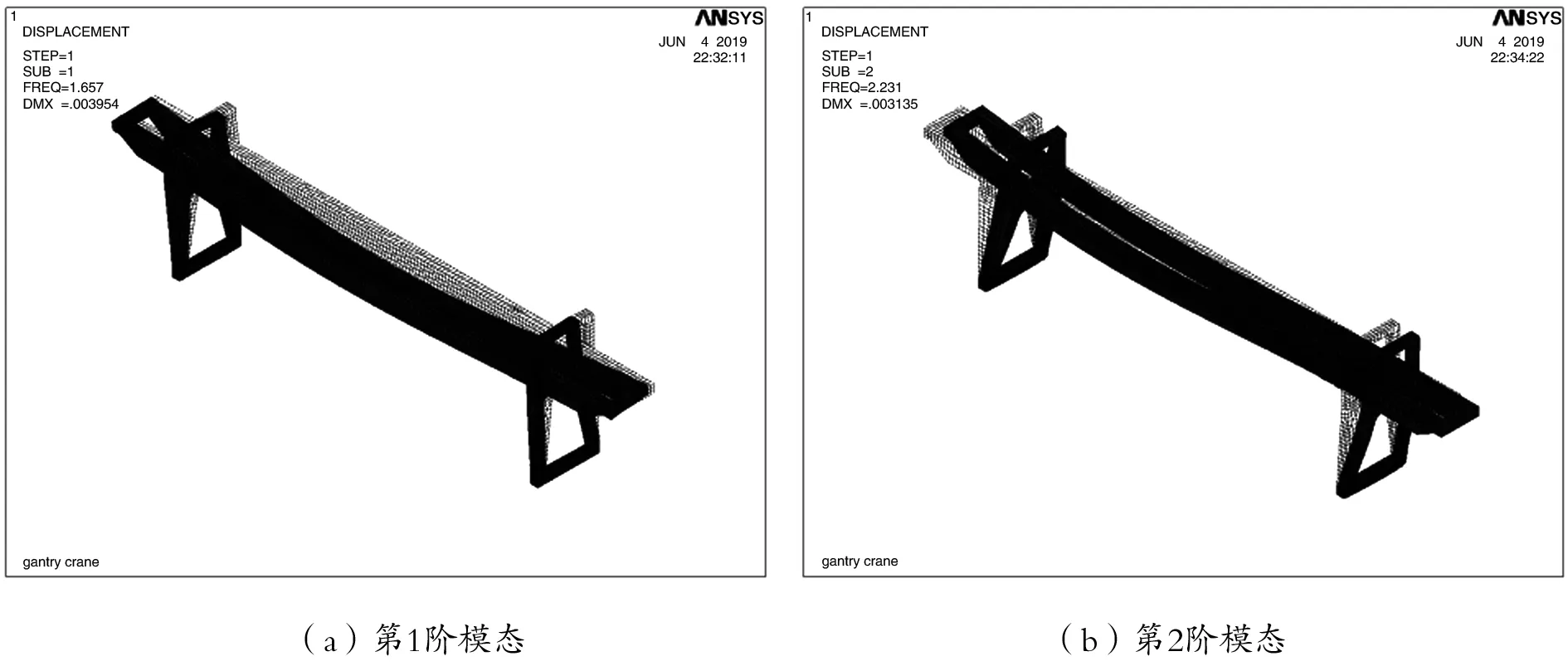
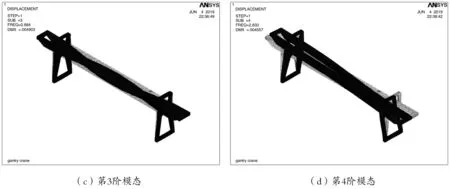

图5 门机金属结构模态振型图
从图5可以看出,该门机金属结构的各阶振型表现如下:第1、4、5阶振型均为整机在前后方向(沿大车轨道)的摆动及主梁在水平面内的一阶弯曲,第2阶振型为整机在左右方向(沿小车轨道)的摆动及主梁的一阶弯曲(在竖直平面内),第3阶振型为主梁的一阶弯曲(在水平面内),第6阶振型为主梁在竖直面内的一阶弯曲。
五、门式起重机金属结构谐响应计算结果
为了考察外界激励载荷作用下,该门机金属结构的动态响应,找出结构动态特性更为敏感的模态,针对该门机金属结构,开展了谐响应分析。分析时设置外界激励频率范围,考虑到模态分析结果中提取的门机结构前六阶固有频率最大值为3.9252Hz,故将外界激励载荷频率变化范围设置为0~4Hz,变化极差为0.1Hz,图6给出了该双梁门式起重机金属结构主梁中部节点竖直方向的位移响应幅值—外界载荷激励频率曲线,从图6可以看出,其位移响应幅值在激励频率为3.9Hz时达到最大,与上述整机金属结构模态分析结果进行对比发现,该门机金属结构的第6阶模态固有频率与激励频率3.9Hz接近,所以,可以认为该门机金属结构的动态特性对第6阶模态更为敏感,在对结构进行优化设计时应该重点分析该阶模态的影响。

图6 主梁中部节点位移响应幅值(竖直方向)
六、结语
本文利用有限元软件ANSYS,对某双梁门式起重机金属结构的静、动态特性进行了分析,计算了该门机金属结构在工作载荷作用下的静强度、静刚度、模态固有频率及振型等指标参数。通过分析得出如下结论。无论起重小车位于主梁跨中还是悬臂端,该门机金属结构在工作载荷作用下承受的最大工作应力均没有超过该材料的许用应力值,即,该双梁门式起重机金属结构的静强度特性满足设计要求。当起重小车位于主梁跨中时,主梁金属结构产生的位移变形最大。该门机金属结构在约束状态下的前六阶固有频率分别为1.6567、2.2315、2.6844、2.8328、3.4355、3.9252Hz,其中,第1、4、5阶振型均为整机金属结构的摆动(沿大车轨道方向)及主梁的一阶弯曲(在水平面内),第2阶振型则为整机的摆动(沿小车轨道)及主梁的一阶弯曲(在竖直面内),第3阶振型为主梁的一阶弯曲(在水平面内),第6阶振型为主梁的一阶弯曲(在竖直面内)。该门机金属结构的振动响应幅值曲线在外界激励载荷频率为3.9Hz时,达到了最大峰值,结构的第6阶模态固有频率与该激励频率最接近,该结构的动态特性阶对第6阶模态更为敏感。
