基于特征结构配置的飞机横航向控制律设计

翁雪花，项国辉，邹俊俊，余云鹏

（航空工业洪都，江西 南昌，330024）

0 引言

控制律设计是电传/自动飞行控制系统的核心技术之一，一直受到设计人员的高度重视。迄今为止，控制律设计依据主要是经典控制理论和现代控制理论。

经典控制理论是针对单输入单输出 （SISO）的线性时不变系统，经典控制理论主要包括：劳斯（Routh）稳定判据、Nyquist分析、根轨迹法、频率法（Bode图）等。目前，控制律设计在工程实践中所使用的方法为调参法。控制律一般为PID结构，控制参数设计通常使用极点配置方法、根轨迹分析法等较为经典的方法。

随着飞行包线的不断扩展及新型飞行器的不断出现，控制律设计面临的挑战不断增加，现代控制理论和方法的应用研究不断得到重视。现代控制理论较经典控制理论的应用范围广，既可用于单输入单输出（SISO）的线性时不变系统、也可用于多输入多输出（MIMO）的线性/非线性系统、时不变/时变系统。现代控制理论主要包括：线性系统理论、最优控制理论、非线性系统理论、随机控制理论、自适应控制理论、鲁棒控制理论等。

本文研究具有工程应用前景的控制方法——特征结构配置方法。

1 基于特征结构配置的控制律设计方法

特征结构配置方法是一种基于时间域的多变量系统设计方法，通过对线性系统配置不同的特征向量及特征值，将期望的系统性能和解耦要求转化为特征值和特征向量，类似经典控制理论中的零极点配置。

结合飞机的飞行品质中对飞机方程特征值等的要求，特征结构配置可直接选择适当的特征值和特征向量，使飞机能够实现预期的动态响应特性。在飞机的特征结构配置中，选择的特征值能够实现控制系统的稳定，特征向量能够实现控制系统动态响应的解耦，二者一起保证系统的动态性能。因此，特征结构配置方法在飞行控制系统设计中有着广阔的应用前景。

本 文 以 某 型 教 练 机 5km、0.216M，5km、0.3M，5km、0.9M三个状态点为例，应用特征结构配置方法设计飞机横航向的控制律。

1.1 特征结构配置方法描述

对于系统

其中，x为n维状态向量；u为r维输入向量，y为m维输出向量；A为n×n维的常数矩阵、B为n×r维的常数矩阵、C为m×n维的常数矩阵、D为m×r维的常数矩阵。

其状态反馈控制律为

则有

其中，A∈Rn×n、B∈Rn×m、K∈Rm×n、G∈Rn×n、x∈Rn×1、u∈Rn×1。 若G具有n个互异特征值 λi，i=1,2,…,n，其对应的特征向量为vi，则有

特征结构配置方法即寻找K，使得G即(A+BK)含有规定的特征值和特征向量。

1.2 基于特征结构配置的控制律设计

依据特征结构配置方法，首先选择期望的特征值和特征向量。 选取状态变量x=[β ωxωyγ]，n=4，控制输入为u=[δxδy]。

由GJB 185-86一级标准规定，最小无阻尼自振频率ωnd不小于 1.0，阻尼比 ζd不小于0.19，阻尼ζd*ωnd不小于0.35，滚转模态时间常数不应大于1.0s，最小螺旋模态倍幅时间应大于12s。选择荷兰滚特征根为-2.5±2.5i，对应的荷兰滚阻尼比为 0.7071，荷兰滚频率为3.5355，滚转特征根为-3，对应的滚转模态时间常数为0.33s，螺旋特征根为-0.002，对应的螺旋模态倍幅时间为500s，则期望的特征值：

由特征结构配置方法可知，令与上述期望的特征值所对应的特征向量中需要解耦的模态元素为零，就可以得到满足要求的解耦设计结果，使控制系统具有期望的动态性能。为了使横向与航向解耦，选择与期望特征值所匹配的特征向量如式（6）：

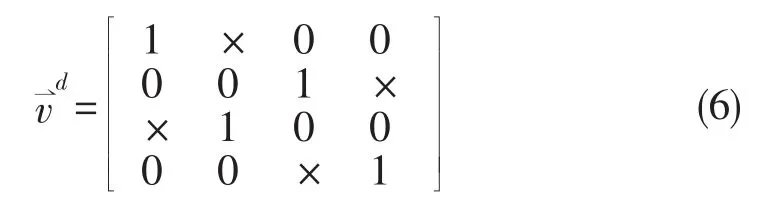
其中“×”表示未受约束（即任意的）项，而所有其他值（包括“0”）表示严格的特征向量约束。

其中，是特征向量中严格约束的元素组成的向量，是中未受约束的元素组成的向量，i=1,2,3,4。

对于第i个特征值对应的 2（rank（B）=2）子空间L，如式(8)所示。

将期望的特征向量投影到上述重新排序后的子空间，可得可达到的特征向量，即

式(10)中选择的要使得性能指标最小化，则有

对每个不同的特征值λi，可以得出相应的。将统一起来，且组成一个矩阵。

最后，计算反馈增益矩阵。

由于矩阵B的秩为r（r=2），小于n，引入线性变换T=[B…M]，使得变换后的矩阵的秩为n，则

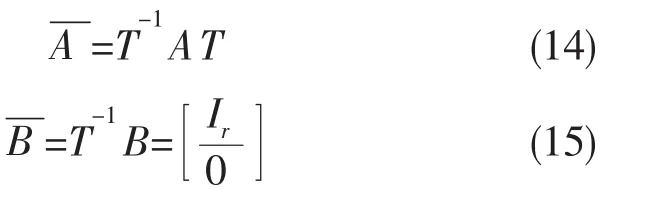
变换后实际特征向量为

其中是变换后特征向量的前r个元素。

选择变换后矩阵前r行，则有

综上，通过计算，可得到基于特征结构配置的反馈矩阵K为

2 仿真验证

基于上述方法得到的控制律，在MATLAB Simulink下搭建模型，该模型包括控制系统、作动器和飞机方程，框图如图1所示。

图1 仿真模型示意图

2.1 仿真分析

分别输入10°/s的滚转角速率指令和1°的侧滑角指令，三个状态点的仿真结果如图2和图3所示。

图2 10°/s滚转角速率指令仿真结果

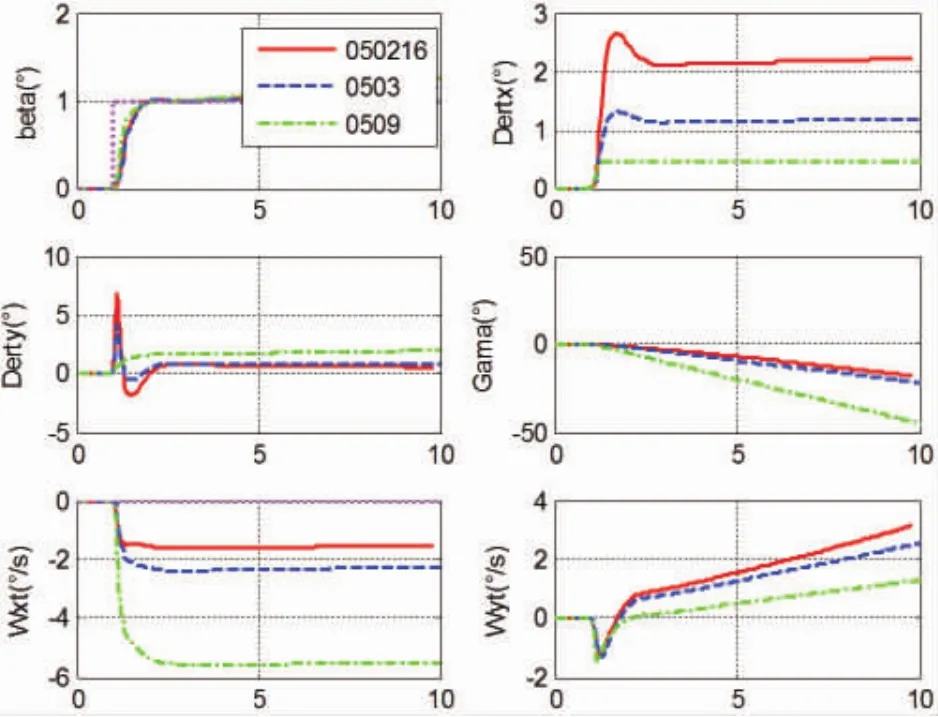
图3 1°侧滑角指令仿真结果

由仿真结果可知，当给定10°/s滚转角速率指令时，飞机滚转角速率能够迅速跟踪指令，且曲线平滑，几乎没有稳态误差，同时产生的侧滑角较小；当给定1°侧滑角指令时，飞机侧滑角能够平滑、较好的达到所给定的指令值，几乎没有超调，响应速度快，同时产生的滚转角速率较小。由此可以验证该方法能够较好的实现横航向解耦。

2.2 对比分析

以0503状态点为例，将基于特征结构配置得到的反馈控制律与经典理论方法设计的控制律仿真结果对比，如图4和图5所示。

图4 10°/s滚转角速率指令仿真对比

由对比结果可以得到，当给定10°/s滚转角速率指令时，基于特征结构配置方法能够较为平滑的达到指令值，而经典理论方法的响应速度较快，但存在超调，前者同时产生的侧滑角较小，较好的实现了横航向解耦；当给定1°侧滑角指令时，二者的响应速度相当，基于特征结构配置方法的曲线较为平滑，不存在超调。

图5 1°侧滑角指令仿真对比

3 结论

基于特征结构配置方法得到的控制律能够平滑的跟踪指令，响应速度快且能够较好实现横航向解耦。较经典理论，该方法能够一次性求出反馈系数，且在所求出的反馈控制律下，飞机响应平滑迅速，再根据飞行品质计算结果调整优化个别参数，缩短了控制律设计的时间，提高了效率。