教练机飞行性能指标论证方法研究

蒋盼盼，刘 卓

（航空工业洪都，江西 南昌，330024）

0 引言

教练机作为飞行员训练的主要装备，很少直接参加空战或担负空中打击任务，其焦点是将飞行学员快速培养成技能娴熟的飞行员，因此其飞行性能指标（下文简称“性能指标”）论证方法与战斗机的相比，既有相似性又存在显著不同。现代教练机是系统配套、体系化发展的[1]，飞行员过渡到更高学习阶段需要经历一段过渡转换时间[2]，如果该阶段与前一阶段飞机性能衔接合理、过渡光滑，飞行员状态转换时间会明显缩短，训练效率会更高。这也意味着，教练机性能指标论证除了需考虑使命任务要求、经济性要求、未来较长时间内的前瞻性和可扩展性要求外，还需着重考虑教练机在训练体系中的衔接性要求[3]，以期实现技能“正迁移”和高效训练。

教练机作为一种训练装备，其相对目标机（本文的目标机指教练机向上衔接的机型，如基础教练机的目标机为高级教练机，高级教练机的目标机为战斗机等）来说担当从属作用，而目标机的发展演化和更新换代，本身也具有特有趋势，因此教练机性能指标论证不能针对单机平台进行定性描述，而应将教练机特性与目标机特性关联起来，寻找一种系统性量化方法，为确定科学、合理的教练机性能指标提供决策依据。目前虽有公开的文献针对通用飞机/战斗机的性能指标进行论证，但尚未有针对教练机性能指标论证方法的研究，如代桂成等[4]参考国内外多个超轻型飞机适航标准，提出了超轻型飞机性能要求。杨华保[5]基于原准机数据的修正采用重量分析方法对战斗机的性能指标进行了分析论证。黄俊等[6]以训练效能为目标函数对高级教练机的性能指标进行了优化。以上相关研究虽为论证教练机性能指标提供了借鉴和参考，但其或侧重于单机平台，或侧重于类比，或侧重于性能指标的优化，未介绍关注衔接性的性能指标从无到有的论证过程。基于此，本文提出了一种系统性定量分析教练机性能指标的方法——关联预测法，其综合考虑了以下三个方面：一是教练机之间的体系定位和配套能力，二是与作战飞机的衔接性，三是未来较长时间内的前瞻性和可扩展性。该方法以最优化准则为核心，能够合理论证满足当前和未来需求的初步教练机性能指标，为后续教练机性能指标的进一步优化和确定提供可靠的初始数据。

1 关联预测法理论分析

关联预测法的研究对象不再是单机平台，而是相互之间有关联的“飞机对”。方法的本质是关注教练机与目标机间的协调性，以及这两类飞机特性之间的定量联系。通过历史时段教练机与目标机的特性联系总结并检查规律，再根据选定的预测阶段目标机特性值，将规律延伸至未来，获得教练机性能指标预测值。

1.1 数学模型

为了系统性分析教练机与目标机特性之间的联系，首先需确定教练机与目标机“飞机对”集合和规范化的权重系数矢量。“飞机对”可理解成为了使用目标机，而利用该教练机系统培训飞行员的教练机和目标机。每一“对”都对应有自己的权重系数，且与教练机的使用数量、服务期成比例。该方法的核心是确定教练机性能指标矢量的零次最佳一致逼近，可用如下形式描述：

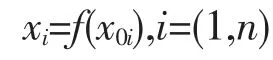
其中：xi——预测的未来时段教练机与目标机对于特性i的关联系数均值；

x0i——历史时段教练机与目标机对于特性i的关联系数均值；

n——教练机特性集合中的特性个数。

根据上式可以得出：

1）从形式上说，该方法在某种意义上是教练机发展所要求的；

2）从方法上说，该方法是目标预测优势和搜索方法的要素结合；

3）从时间上说，该方法所预测的结果应该是短-中期（5～15年）的，因为预测结果的可信时间期限应该不短于研制教练机过程的时间周期（平均5年），且不超过目标飞机更新换代周期（10～15年）。

1.2 方法设计步骤

关联预测法主要由四部分内容构成：原始数据库的建立，相关性检查，构建关联系数及趋势，预测飞行性能值。

1.2.1 原始数据库的建立

1）确定要预测的教练机性能矢量构成

选定要研究的教练机性能参数，也就是矢量={x1i},i=1,2,L,n（n为性能参数总个数），该集合可能受以下几个方面的支配：必须准备估算教练机训练效能用的初始数据；对性能参数的计算方法研究的充分程度；历史数据可查性等。

2）形成教练机和目标机及其“飞机对”的客观历史数列

选定教练机{X1i}，i=1,2,L,N1，它与一定的目标机{X2i},i=1,2,L,N2有关，其中N1，N2表示历史时段教练机总数和目标机总数，X1i、X2i表示历史时段教练机型号和目标机型号。从中分出N对“飞机对”，将这些“飞机对”与特定时间联系在一起，就构成了“飞机对”的客观历史数列。

基于以下两点考虑，客观历史数列选择前期50年：

（1）如前所述，预测是短-中期（5～15 年）的结果；

（2）为保证预测结果的精度和可靠性，历史时段应比要预测的未来时段长好几倍。为便于分析和构成后续的预测并检查其正确性，以10年分段，并且将N对“飞机对”分成两个数列——前4个10年的N0“对”为教练数列，最后一个 10年的Nk“对”为检查数列。

3）构成“飞机对”的性能矢量数据库

使用上一步选取出来的N对“飞机对”，以及它们协同使用的时间点，查找或计算n个性能值：{x1ij},{x2ij},{tij}，i=1，2，L，n，j=1，2，L，N， 其中x2ij为目标机性能矢量，tij为性能指标x1ij与x2ij协同使用的时间点。所有飞机的同类性能应按同一方法计算，否则由于计算误差的差异，这些性能的未来预测趋势可能逐渐失真。

1.2.2 相关性检查

相关性检查目的是理清“飞机对”的性能指标联系。数据库建立好之后，就可以定量估算教练机与目标机性能指标间的规律关系。一般情况下，教练机性能指标矢量与其成对的目标机性能指标矢量={x2i}，i=1，2，L，n的联系，可表示为=M·其中M为关联矩阵，由此可以得出，教练机的任意性能指标x1P，p=1，2，L，n与目标机特性集之间可认为是线性关系：

教练机和目标机性能存在线性关系的假设，可以通过相关性检查进行检验。基于相关分析法，分析历史时段中每个10年段相同性能指标下教练机与目标机间的相关性系数，并与对应于选定的置信概率的相关系数门槛值相比较。相关解析结果分析表明，教练机和目标机同样性能指标间，大多数情况下可发现显著的相关性，即第一次逼近时，矩阵M集中在对角线上，因此可认为教练机的特性与目标机的对应性能指标成正比。

1.2.3 构建关联系数和趋势

1）形成关联系数数组

将性能指标的绝对值转化成它们的比值，即关联系数kij=x1ij/x2ij，i=1，2，L，n，j=1，2，L，N。 在大多数情况下，相对于飞机性能与时间之间的关系，关联系数与时间的关系更稳定和单调一些。

2）淘汰非典型“飞机对”的关联系数

针对各性能指标，分析每个10年段出现的关联系数相对均值的正态最大偏差值τi,i=1,2,L,n，并与选定置信概率下的偏差门槛值τT进行比较，淘汰满足τi≥τT的“飞机对”，使预测有更充分的依据。

3）构成关联系数趋势

去掉淘汰掉的关联系数值，构成“飞机对”性能指标关联系数的动态数列。利用筛选后的教练数列构建线性趋势，Ki=aiT+bi，i=1，2，L，n， 其中时间T取各 10年段的平均年份进行计算，Ki表示在T时刻由趋势确定的对于特性i的关联系数值，ai，bi分别表示线性比例系数和常数分量。

由于计算的性能值有误差，也就是说关联系数的计算有误差，而“飞机对”协同使用的时间也不能认为是准确的，所以不能使用常用的最小二乘法计算ai、bi，i=1，2，L，n。不同构建方法的分析结果表明，此时采用 wald 回归法计算ai，bi，i=1，2，L，n最为合适。

4）检查趋势形式选定的可靠性

使用wald检验法检验趋势选定的可靠性，具体公式如下：

其中，Nl——第l（l=1,2,3,4）个10年段内的“飞机对”数量；Tl——第l个10年段的平均年份；kij——第l个10年段中关于特性i的第j个关联系数；F0是给定置信概率下的F分布值。

如果上式的检查结果否定，就返回上一步，重新选定一种线性趋势，并计算ai、bi,i=1，2，L，n。

5）检查趋势的预测性能

1.2.4 预测教练机性能指标矢量

基于战术技术任务书或通过科学预测的方法选定未来目标机性能指标矢量={x2Yi}，i=1,2,L,n，再根据预测的关联系数值KYi=aiTY+bi,i=1,2,L,n，获得零次逼近的预测阶段教练机性能指标矢量={x2Yi×KYi},i=1,2,L,n。

通过关联系数得到的零次逼近的教练机性能指标矢量，着重考虑了教练机在训练体系中的衔接性要求，不仅反映了教练机解决传统问题的能力，也反映了现有教练机在训练效能方面已实施的方法和措施。但是，关联预测法的分析结果具有综合性特点，其无法考虑更特殊情况，特别是对形成教练机性能矢量非常关键的那些因素，如飞行员训练大纲的特点，不同国家和不同代飞机的差别很大；还有教练机战技任务书中包含的特殊要求（如成本限制或某些系统选定限制）。因此，根据先进定位的原则，后续需对零次逼近的教练机性能指标矢量作进一步优化和最终确定。

2 算例分析

考虑到飞行性能参数以及“飞机对”客观历史数据众多，为更快速、有效的运用该方法，本文在Matlab平台上对该方法进行算例数值计算。以研究2015年左右的配装涡桨发动机的基础教练机为例，相应的目标机选定为某型高级教练机。

根据新型基础教练机的需求定位、使用特点及可能得到的用于构建基础教练机和目标机 “飞机对”集合的统计数据，算例选取的未来基础教练机主要特性包括失速速度(放襟)、实用升限、海平面最大爬升率等9个参数。图1～图2是2015年左右失速速度（放襟）和海平面最大爬升率关联系数的计算结果，KI-KV为回顾历史时段的关联系数均值。图1中所显示的失速速度(放襟)关联系数值增大，主要是由于目标机大迎角飞行能力增强，左边界能力显著提高。图2中所显示的海平面最大爬升率关联系数值减小，主要是由于目标机机动性能增强及发动机可选性更大，计算结果与实际情况相符。

图1 失速速度(放襟)关联系数随时间变化趋势

图2 海平面最大爬升率关联系数随时间变化趋势

为了进一步验证预测结果的合理性，统计了国外同时期同类涡桨基础教练机的飞行性能参数，获得各性能参数参考区间[7]，如表1所示。

从表1可知，预测的失速速度(放襟)、海平面最大爬升率性能指标与同时期同类型的教练机基本相当，可以认为该预测结果相对准确，进一步检查了预测方法的合理可信性。

3 结论

通过对教练机性能指标论证特点的分析，建立了一种系统性量化分析未来教练机性能指标的方法，并进行了算例计算，得到了以下结果：

1）该方法以最优化准则为核心，充分考虑了教练机性能指标在训练体系内的衔接性特点以及未来较长时间内的前瞻性和可扩展性。

2）该方法预测的性能指标科学、合理，可为性能指标后续进一步优化和最终确定提供可靠的初始数据。