PISA数学素养测试与上海中考应用题的比较研究

杨永泽 王金才

【摘 要】

本文对国际大规模数学测评PISA和新课改后上海中考应用题进行比较，发现上海中考应用题的科学背景相对较少，而PISA测试背景分布更加均匀;PISA中选择题比重较中考应用题大，有部分开放式构答，而上海中考应用题以封闭式构答为主，目前未出现开放式构答;上海中考应用题侧重考察学生对基础知识与基本技能的掌握情况，而PISA更关注学生对原始问题的分析处理能力;上海中考应用题的难度稍低于PISA难度.并对上海中考应用题的命制提出若干建议。

【关键词】 PISA;上海中考;应用题;比较研究

1 问题提出

PISA是由国际学生评估项目与发展组织（OECD）统筹的对15岁学生能力的国际评估计划，是一项以改善教育政策为导向的跨国测评研究项目，在国际教育评估上的影响力越來越大，引起教育工作者的广泛关注.2012年国际学生评估项目PISA测试的主项为数学素养，其测试题目均具有实际背景，着重考察学生在实际生活中创造性地运用数学知识和技能的能力，测评主要包含数学情境、内容、过程三个维度.

我国中考主要考察义务教育结束后学生对基础知识、基本技能、基本方法的掌握和学科能力，并为全面体现出对初中毕业生相应数学学业质量的监控及反馈而持续推进课程评价改革.“能够运用所学知识解决简单的实际问题”是初中数学教学的目标之一，要求让学生体会数学与现实生活的紧密联系，增强应用意识，提高运用数学知识与方法解决问题的能力.并且随着课程改革的逐步深化，中考命题也更加重视对应用题的命制与改革[1].

本文对实施新课改后上海中考最近八年的应用题与PISA数学素养测试样题进行对比研究，希望可以为中考应用题的进一步发展和改革提供一些思路与建议.2 数学中考与PISA数学素养测试整体比较

首先，以2019年上海市数学中考为例，与PISA数学素养测试进行整体比较，结果如表1所示.

PISA数学素养测试与上海市数学中考的测试目标、试题背景、评卷理念均有所不同.但从内容维度上来看，PISA数学素养测试与上海市数学中考在数、几何、代数、数据四个核心知识领域上有着基本共识，体现出对学科能力、数学思维过程、认知水平以及数学素养的培养上起着基础性作用的知识领域的重视.上海市数学中考或其它地区中考均会将几乎每一题都对应在具体数学内容之下，要考察的知识容量更大而且要求也更高.由于各国数学课程有所不同，所以PISA测试中未看到更细化的具体知识内容，只是一些简单描述[2].PISA数学测评内容领域每个维度可能会横跨中考数学多个内容维度.从这里可明显反映出PISA数学测评不以数学课程内容为主导的测评特征[3].可以看到，中考与PISA这两种大规模测试的目标、试题背景、评卷理念等都有所不同，两种测试均具有各自的意义与价值.所以我们并不能将PISA数学测试盲目照搬到国内中考数学上来，但二者仍有一些共同之处，因此我们依然可以从PISA数学测试中获得一些对于中考数学试题命制，尤其是应用题方面的启发.2 上海中考应用题与PISA数学素养测试题的比较

数学应用题是中学阶段体现数学应用性的典型内容，是学生了解数学应用的窗口，也是检测学生应用意识和能力的重要方式.由上述分析可以说明这两项测评的考查内容大部分是相同的，但PISA更加强了对分析过程的考察.本文统计了实施新课改后2012—2019年上海市中考数学试卷中的全部共计38道具有实际背景的题目与PISA测试题的主要调查项目26题，从题目背景与题型、题目难度、“数学化”水平三个方面进行比较分析.3.1 题目背景与题型

本文按照PISA的分类标准对两个测试的题目背景进行分类统计.PISA将问题背景分为个人、社会、职业、科学4个维度.直接和学生个人日常生活有关的题目背景被归为个人类，比如掷骰子、摸球等.社会情境则和当地或者广泛的社群有关，需要学生观察周围社会环境的某些层面或环节，比如天气预报、唱片销量、体育竞赛、彩票等都属于社会情境.工农业生产、产品数量与质量、商品销量等与工作场合有关的问题属于职业情境.科学情境则较为抽象，指将数学用于自然世界、科技领域以及技术过程和理论研究的情境，如人口数据、地震数据、医学数据、各种垃圾自然分解的时间等等[4].按照上述分类标准，对两个测试的题目背景进行分类统计之后的结果如表2所示.

由表2可知，PISA使用的四种背景比例相差不大.上海2012-2019年的中考应用题所使用的背景则更贴近学生的个人日常生活和社会问题，而科学背景相对较少.具有科学背景的应用题能够引导学生进行跨学科知识的整合，提升应用数学于自然世界、科技领域等方面的意识，对于提高学生的科学素养，促进学生后期发展都具有重要作用，因此中考应用题也应该尽量选取更多的科学背景.

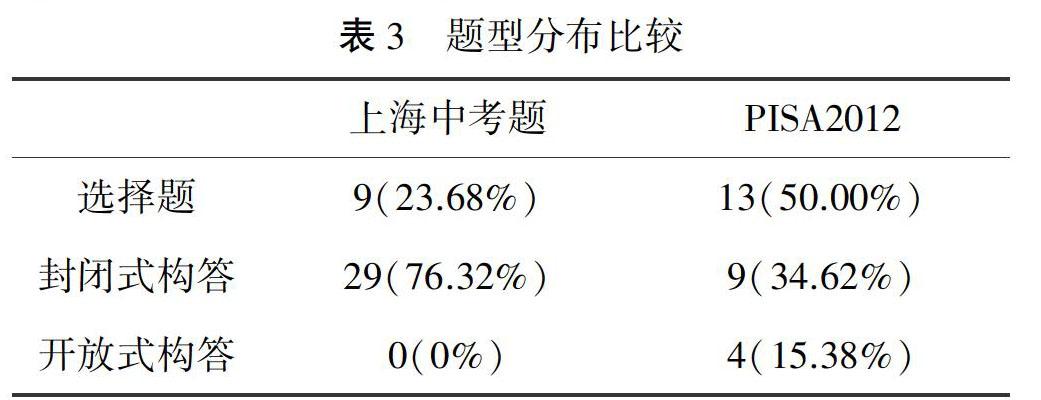
PISA的题型分为开放式构答、封闭式构答和选择题三种形式.其中开放式构答指需要学生有一些扩展性回答的题目，比如学生需要写下步骤或者解释如何得到答案;封闭式构答指提供结构化设置的题目，学生容易判断正确与否，比如要求学生处理的数据是出题者设置的简单数据;选择题指提供了一个或多个选项供学生选择的题目[5].据此对两份测试卷进行题型分类统计，结果如表3所示.

可以看出，PISA中选择题比重较大，而中考应用题以封闭式构答为主，目前未出现开放式构答.主要由于开放题的标准答案的设置以及批改还存在一些问题，而PISA对开放题的评价有严格的编码及评价标准，这是可供借鉴的.3.2 题目“数学化”水平

本文采用从“数学化”水平高低，建立数学模型难易的角度将应用题分为四个层次[6]：（1）直接套用现成公式计算;（2）数学模型在问题情景中已经给出，只需利用现存的数学模型对问题进行定性、定量分析而求解;（3）对于已经加工提炼的，忽略了次要因素，保留下来的诸因素之间数学关系比较清楚的数学问题，建立数学模型，这类问题可以说已经做了初步的“数学化”加工，还需要解题者进一步“数学化”;（4）需要对原始的实际问题进行分析加工，提炼出数学模型，再分析出数学模型进行求解.将以上四个层次分别用水平一、水平二、水平三、水平四表示，如图1所示.可以看到从水平一到水平四，应用题的“现实化”程度越来越高，人为加工逐渐减少，同时对学生“数学化”、建立数学模型的能力要求也越来越高.

对上海中考应用题和PISA数学素养测试题目的“数学化”水平进行归类统计后，结果如表4所示.

经统计发现上海数学中考应用题的“数学化”层次主要集中在前三个水平，虽然中考应用题需要学生进行一定的数学化，但总体上试题还是经过很多人为加工的，几乎不涉及需要学生自己从原始问题出发分析建立数学模型并加以求解，往往条件清楚准确，不多不少，结论唯一确定，原始问题数学化的过程简单、清楚、明了，解出的结论也很少要求学生思考是否符合实际，侧重考察学生对基础知识与基本技能的掌握情况.而PISA数学素养测试的“数学化”水平虽然也集中在第二个水平，但与上海中考应用题相比则明显更侧重于对水平四的考察，更关注学生对原始问题的分析处理能力.近年来，虽然我国毕业考试题目开始尝试从“知识立意”向“问题立意”和“能力立意”进行转移，但推行得比较缓慢[7].其中，一个非常重要的原因是：试题描述的“问题”往往远离学生的真实生活，“能力”的界定和培养也比较模糊.应用题编制的出发点是“应用能力立意”，但体现应用能力的层次还比较低，范围也比较窄，仍属于应试型的那一类题目[8].而PISA测试以单元的形式进行编排，每个单元创设一个复杂且具有关联性的情境，并且这个情境完全来源于实际，并没有人为地编造虚假情境来禁锢学生的想象力，体现了“数学源于生活、寓于生活、服务于生活”的思想，这都是值得国内中考应用题学习与借鉴的.3.3 题目难度

引用史宁中教授在2005年建立的课程难度模型[9]研究的基础上，研究PISA试题和中考题的难度，题目难度模型如下：

N=αS/T+（1-α）G/T，

其中N表示测试卷的难度，S表示测试卷的知识深度，G表示测试卷的知识广度，T表示完成测试卷所需时间，α表示权重.

由于PISA定義的数学过程包括表征、应用、诠释三个方面，所以测试卷每道试题的知识深度分为“表征、应用、诠释”三个水平，赋值分别为1，2，3，用其平均值作为测试卷的知识深度;测试卷的知识广度由知识点含量决定，每道题目含一个知识点赋值为1，含有2—3个知识点赋值为2，包含4个知识点及以上赋值为3[10].测试卷的时间表示学生完成该试卷所规定的时间，PISA所选的题目需要60分钟，而一次中考题的考试时间共100分钟，按其中应用题所占比例计算约为16分钟，由于统计的是8年的应用题，故将时间记为128分钟，计算结果如表5所示.

由表4可知，上海中考应用题的知识深度低于PISA，设α为0.5后根据模型进行计算可得上海中考应用题的难度为0.25，而PISA难度为0.27，上海中考应用题的难度稍低于PISA难度.4 总结与建议

本研究通过对上海最近八年的中考数学应用题和PISA测试题的对比分析，发现在考察学生应用数学的能力时：

1.上海中考应用题的科学背景相对较少，而PISA测试背景分布更加均匀.

2.PISA中选择题比重较中考应用题大，有部分开放式构答，而上海中考应用题以封闭式构答为主，目前未出现开放式构答.

3.上海中考应用题侧重考察学生对基础知识与基本技能的掌握情况，而PISA更关注学生对原始问题的分析处理能力.

4.上海中考应用题的难度稍低于PISA难度.

经过PISA测试题的启发，本文对中考应用题的命制也给出了以下建议：

1.应用题背景的取材要力求真实

问题情境的创设一要真实，二要使学生有经验地体验，这样才能逐步加深学生对数学本质的理解[11].因此，在进行应用题的命制时要注意在观察、搜寻中广泛搜集素材，力求背景的真实性而非人为生搬硬套，这就需要命题工作者对可能用到的背景材料进行长期积累.

2.应用题要让学生经历“数学化”的过程

中考数学应用题的编制可以从PISA测试中“取经”，为学生搭建体会问题分析过程的平台，给学生留有一定的思考空间，营造较为真实的情境，让学生能经历从分析问题到解决问题的完整“数学化”过程，而不是只关注得出最后的结果.

3.增加应用题的科学情境

“学科交织”是构造具有科学情境的应用题的重要方式，比如可以用数学解决物理、化学等学科的问题，引导学生进行跨学科知识的整合与迁移，发展学生的科学意识与科学素养.这对学生的长远发展均具有重要作用.

4.增设开放题

逐步增加一些开放式应用题，如题目结论不唯一或情境条件不充分的应用类试题，发展学生的批判思维和创新思维，以弥补当下中考试题对学生创新批判能力考察不足的问题.

参考文献

[1]李忠前，张晓燕.中考应用题命题思路及赏析[J].中国数学教育，2011（10）

[2]黄华.从PISA数学素养测试对国内数学教学的启示——PISA数学素养测试与上海市初中毕业统一学业考试数学测试之比较[J].上海教育科研，2010（5）

[3]王鼎.上海中考数学测评和PISA数学测评成绩差异性研究——基于PISA2012年的测评结果[J].外国中小学教育，2017（6）

[4]李俊，黄华.PISA与上海中考对统计素养测评的比较研究[J].上海教育科研，2013（12）

[5]沈阳，喻平.PISA2012与我国数学中考题的比较与思考——以南京市试题为例[J].数学通报，2017（01）

[6]沈文选.关于中学数学应用研究的几点思考[J].数学教育学报，2000（01）

[7]孔凡哲.PISA对我国中小学考试评价与质量监控的启示[J].外国教育研究，2005（05）

[8]梅松竹，王燕荣.我国数学试题与PISA数学试题的比较及启示[J].数学通报，2012（06）

[9]史宁中，孔凡哲，李淑文.课程难度模型：我国义务教育几何课程难度的对比[J].东北师大学报，2005（06）

[10]郭民，史宁中.中英两国高中数学教材函数部分课程难度的比较研究[J].外国中小学教育，2013（07）

[11]付钰，张景斌.PISA2012数学测试题的分析与启示[J].中国数学教育（初中版），2019（09）

作者简介 杨永泽（1998—），女，硕士研究生，研究方向为中学数学教育.

王金才（1966—），男，副教授，博士.