一种新的复杂网络建模和特征提取方法及应用*

田 甜， 温广瑞,2， 张志芬， 徐 斌

(1.西安交通大学智能仪器与监测诊断研究所 西安，710049) (2.新疆大学机械工程学院 乌鲁木齐，830047)

引 言

旋转机械在大型石油、化工、电力、冶金等行业应用非常广泛，是这些企业的核心设备，如果其发生故障不仅影响机器本身的运行，而且还会对后续生产造成损失[1]。因此，对旋转机械进行故障诊断具有重要的实际意义。 旋转机械振动信号的非平稳特性往往导致故障难以精确识别。时频分析、小波都是有效处理非线性非平稳信号的方法[2]，但均存在不同程度的缺陷，如小波分析中小波基的选取直接影响分析结果，而且基函数一旦选定在分析中便不能更改，不具备自适应特性[3]。

复杂网络是一种新的分析非线性非平稳信号的方法，可以将信号的波动特性转换为网络的拓扑性质，克服了传统时频分析存在的缺陷，具有简单直观、普适性好、拓扑性质明显及网络结构鲁棒性强等优点[4]。Lacasa等[5]提出可视图建网方法，处理数据量较大的时间序列。孙斌等[6]应用递归复杂网络提取滚动轴承的网络拓扑特性，并进行故障识别。Zhang等[7]在复杂网络的基础上提出构建一种船用发动机的故障诊断系统，并通过仿真数据验证其有效性。虽然复杂网络已在非线性非平稳信号分析领域取得了不错的应用效果，但现有的复杂网络诊断方法通常直接基于时域信息，忽略了频域特性，而且提取的特征只具有全局特性，无法体现网络的局部结构，难以保证故障信息的准确提取。

因此，笔者提出了基于频域复杂网络(frequency-domain complex network，简称FCN)分解的子网络平均度提取方法，并将其用于故障识别。该方法借助复杂网络的结构特性来获取故障信号在频域的变化规律，将其转化为复杂网络结构上的统计特性，不受故障机理的限制。滚动轴承故障信号验证结果表明，该方法能够有效提取代表机械不同故障特征的信息，并实现准确区分，为旋转机械的故障诊断提供一种新的有效手段。

1 复杂网络原理

1.1 有限穿越可视图

有限穿越可视图法是一种基于可视图概念的复杂网络建网方法，它的主要思想为：将序列视为直方图，任意2个数据点之间若满足可视准则就连边，不满足就不连边，以此将序列构建为复杂网络模型。可视准则为：网络中2个节点之间的可视线被截断的次数不超过有限穿越视距N，则认为这2个节点之间是连边的[8]。如图1所示，在直方条图中，实线代表2个节点之间未被阻挡，相互可视；虚线代表2个节点之间被阻挡的次数在有限穿越视距之内，也相互可视。

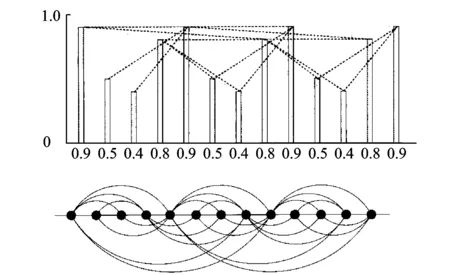
图1 有限穿越可视图算法示意图

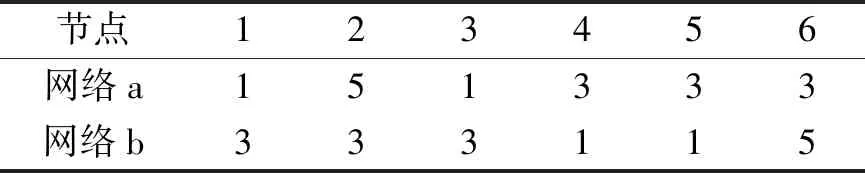
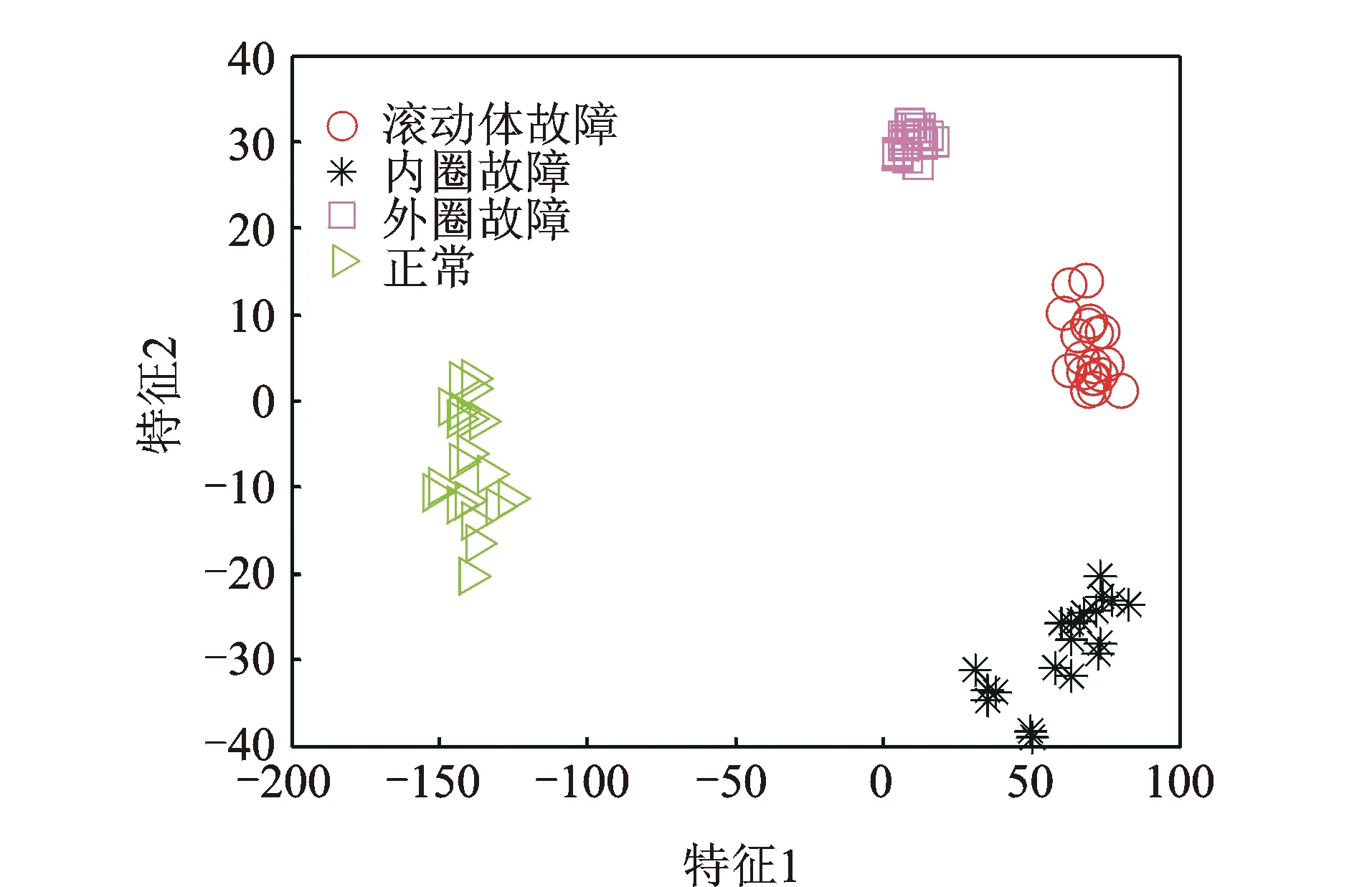
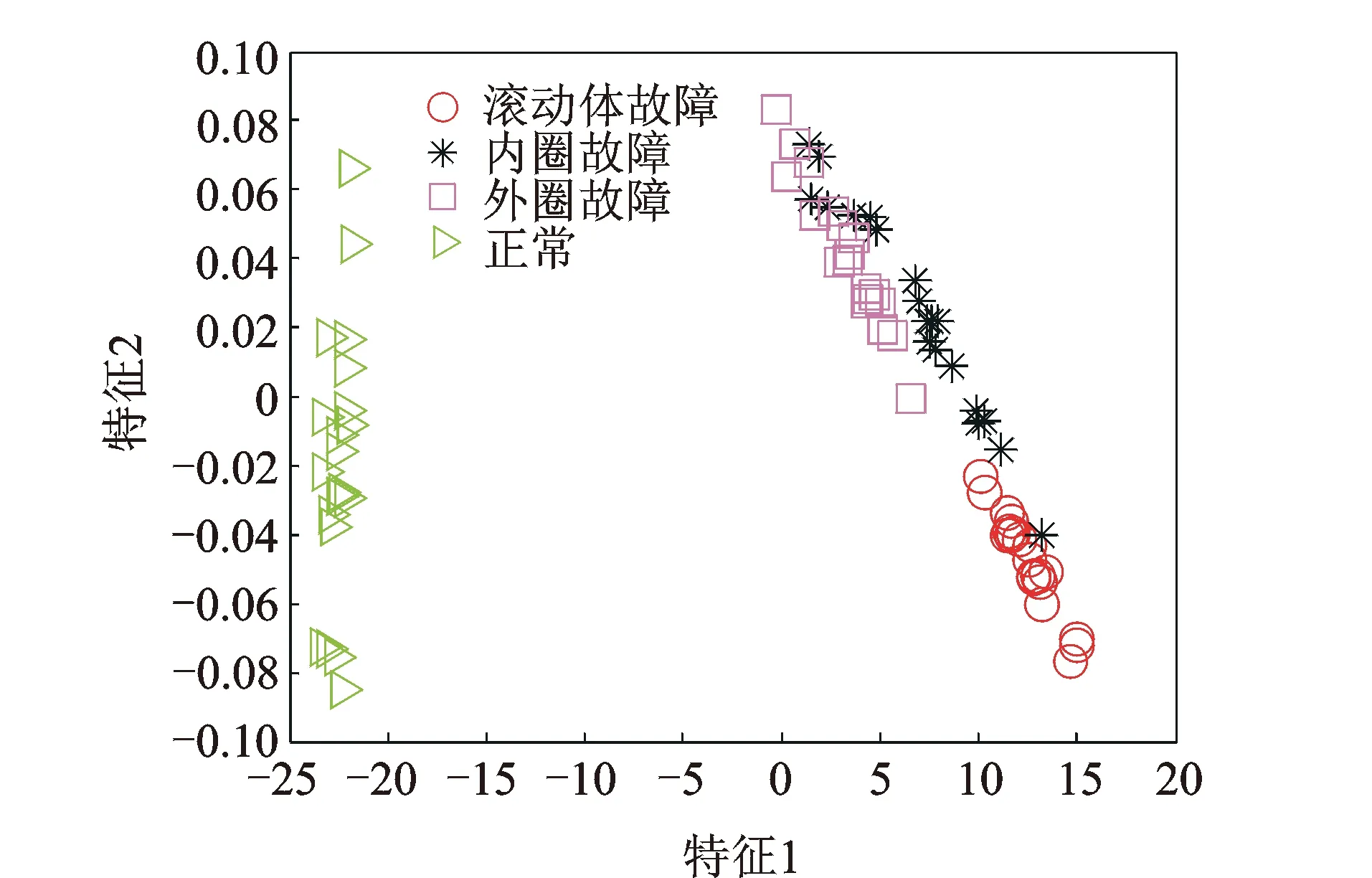
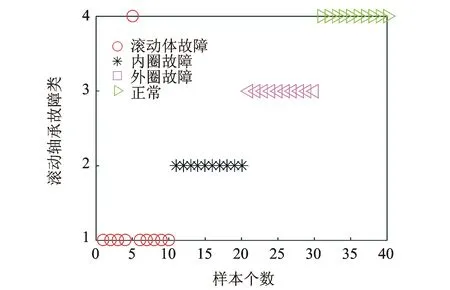
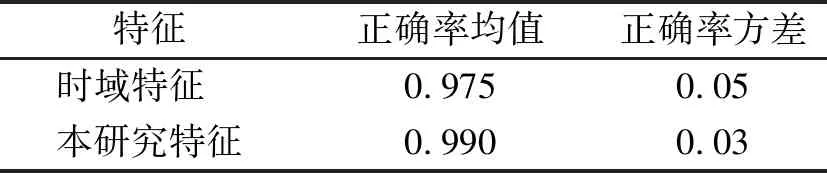
可视准则的数学描述如下：X={xi}i=1,2,…,n为一个有n个数据点的序列，序列中相隔m个数据点的任意2个数据点(ta,xa)和(tb,xb)相互可视，那么这2个数据点之间存在k(k≤N)个数据点(ti,xi)，其中ta

xi>xb+(xa-xb)(tb-ti)/(tb-ta)

(1)

xj

(2)

1.2 子网络平均度

1.2.1 子网络平均度概念

网络的拓扑特性有平均路径长度、聚类系数和度与度分布等，其中度是单独节点的属性中简单而又重要的概念。节点的度ki定义为与该节点连接的其他节点的数目[9]。一个含有n个节点的复杂网络，其平均度为网络中所有节点的度ki的平均值，记为p

(3)

其中：n为网络中的节点总数。

子网络平均度的提取需要在复杂网络分解的基础上进行，网络分解是将已建立的复杂网络模型按照节点的顺序均匀分解为若干个子网络(分解时保留与节点的连边)，然后每个子网络都按式(3)求得网络平均度值，即可得到子网络平均度特征，如式(4)所示

P=[p1,p2,…,pm]

(4)

在确定子网络的个数m时，一般选择m=2l个，且应满足2≤m≤n。

1.2.2 子网络平均度的优势分析

与现有的平均度特征相比，子网络平均度特征可以反映网络在空间上的局部特性，所包含的信息更加丰富，更有利于实现故障识别。图2所示网络均为6节点的网络模型，节点标号为1～6。由图可见，2个网络模型的节点位置相同但节点间的连接不同，网络a中与节点2相连的其他节点数最多，说明网络a的重要节点为2；网络b中与节点6相连的其他节点数最多，说明网络b的重要节点为6。

图2 6节点网络模型

网络节点度分析之前需要计算网络中每个节点的度，计算结果如表1所示。若采用网络中所有节点度的平均值来表征网络，则由式(3)可知，网络a的特征值为pa=(1+5+1+3+3+3)/6=2.67，网络b的特征值为pb=(3+3+3+1+5+1)/6=2.67，即从网络节点平均度的角度来看，网络a和网络b没有区别。因此，网络拓扑特征用节点平均度从全网的角度表征网络模型，存在一定的局限性。

表1 网络节点度

如果提取网络的子网络平均度特征，即可体现2个网络的差异。将网络都均匀分成2个子网络，节点1，2，3及其连边为子网络1，节点4，5，6及其连边为子网络2，分别求出子网络的平均度，并构成一个2维特征向量。由此可得，网络a的特征向量为[2.33, 3]，网络b的特征向量为[3, 2.33]。不难发现，子网络平均度特征可以体现出2个网络在节点连接上的不同，能更准确地反映网络模型的结构特性。

1.3 基于FCN的子网络平均度提取方法

针对旋转机械振动信号的非平稳特性及频域蕴含的丰富信息[10]，笔者提出一种新的基于FCN分解的子网络平均度提取方法，其处理流程如图3所示。

图3 FCN子网络平均度提取方法流程图

具体的处理步骤如下。

1) 计算旋转频率fr=Vr/60，选取频带宽m为fr或fr的整数倍。将1维时间序列X进行傅里叶变换得到频谱Y={yi}i=1,2,…,n，然后对幅值进行逐点平方，在带宽为m的频带内相加，并按顺序排列得到所需频带能量谱[11]，记为E=[E1,E2,…,Ek,…,En]。其中Ek为第k个频带的能量

(5)

2) 设定有限穿越视距初始值N=1，应用有限穿越可视图算法将每个信号对应的频带能量谱映射为复杂网络模型。

3) 根据复杂网络中总的节点数，按照m=2l且2≤m≤n的原则确定复杂网络分解为子网络的个数m。对每个复杂网络模型进行均匀分解，提取如式(4)所示的子网络平均度向量。

4) 类别可分性测度是评价样本特征提取好坏的重要指标，可以选出鉴别性能较强的特征集，类别可分性测度的值越小说明提取的特征集在样本分类方面越有效[12]，因此应用类别可分性测度对特征提取进行评价，定义可分性测度为

J=Sw/Sb

(6)

其中：Sw和Sb分别为类内散度和类间散度。

Sw和Sb的表达式分别为

5) 逐一增加有限穿越视距N，计算对应网络模型下所提子网络平均度特征的类别可分性测度。若求得极小值点，则确定有限穿越视距的取值为该极小值点；若可分性测度值单调，则重复执行步骤3～5，直至出现极小值点。

6) 以步骤5所得有限穿越视距N构建复杂网络模型，并提取子网络平均度特征。

2 数据验证及分析

2.1 轴承信号FCN子网络平均度提取

笔者通过不同故障类型的滚动轴承振动信号来验证所提特征的有效性。采用如图4所示的试验台装置采集滚动轴承故障信号。试验所采用的滚动轴承型号为6308，滚动体个数为8。振动信号由安装在轴承座上的加速度传感器获得，转速为1 050 r/min，采样频率为10 240 Hz。滚动轴承状态共有4类，分别为滚动体故障、内圈故障、外圈故障和正常，其中滚动体故障、内圈故障和外圈故障均为剥落故障，故障直径约为2 mm。试验时，每类采集20个样本，共采集80组数据。

图4 轴承试验台装置

按照FCN子网络平均度提取方法处理滚动轴承的试验数据。首先根据时间序列建立频带能量谱，为尽可能保留数据的周期信息，频带宽选为轴承旋转频率或旋转频率的整数倍，本研究采用的频带宽m是旋转频率的4倍。试验时轴承的旋转速度为1 050 r/min，计算确定频带宽为70 Hz。

在频带能量谱的基础上，应用有限穿越可视图算法构建FCN模型。由于有限穿越视距N的选取直接影响子网络平均度特征的有效性，笔者选用类别可分性测度作为评价函数来确定有限穿越视距的值。如图5所示，类别可分性测度随着有限穿越视距的变化而变化，在一定范围内，当N=3时，类别可分性测度达到极小值，故构建复杂网络模型时，确定有限穿越视距N=3。

图5 有限穿越视距的选取

设置参数频带宽m=70 Hz，有限穿越视距N=3，采用有限穿越可视图算法可得到复杂网络模型所对应的邻接矩阵。对网络作可视化处理，所显示的模型为无权无向的复杂网络模型。设置显示布局为Fruchterman-Reingold，网络节点的大小由节点度决定，度的值越大，节点的尺寸越大，同时颜色也越深。滚动轴承不同状态对应的FCN模型如图6所示。

图6 滚动轴承不同状态的FCN模型

为进一步观察网络模型的重要节点，将图6中的FCN模型局部放大，得到如图7所示的结果。由图7可知，滚动体故障的网络中重要节点为8, 102～105, 189～192, 286；内圈故障的网络中重要节点为6～7, 103～106, 188～191, 286～287；外圈故障的网络中重要节点为101～103, 106,188～189, 191～192；正常状态的网络中重要节点为40, 254。

图7 滚动轴承不同状态的FCN模型局部放大图

滚动轴承不同状态的网络模型，其网络结构与重要节点皆有差异，为网络拓扑特征的提取奠定了良好的基础。

将滚动轴承不同状态的FCN模型进行均匀分解，都分解为16个子网络，提取每个子网络的节点平均度，构成16维特征向量，可以得到如图8所示的滚动轴承不同故障的特征分布图。其中：图8(a)为子网络节点度分布3维图，每个样本提取16维特征，共80个样本；图8(b)为特征分布俯视图，不同颜色代表样本特征的幅值，横轴代表特征，纵轴代表样本，1～20组为滚动体故障，21～40组为内圈故障，41～60组为外圈故障，61～80为正常。

图8 滚动轴承不同故障特征分布图

分别在滚动体故障、内圈故障、外圈故障和正常状态的特征集中选取1个样本绘制其直方条图，如图9所示。由图可知：正常状态与其他3种故障状态的特征有较大的差别；滚动体故障、内圈故障和外圈故障的特征虽然差异较小，但是对外圈故障来说第1维和第16维特征与滚动体故障、内圈故障差异较大；滚动体故障和内圈故障的第6～10维特征差异较大。

图9 16维子网络平均度

2.2 对比分析

2.2.1 特征可分性

采用主成分分析(principal component analysis，简称PCA)算法[13]对子网络平均度特征做降维可视化处理，得到如图10所示的特征降维图，横坐标为第1维特征，纵坐标为第2维特征。由图可知，滚动轴承4种状态同类样本聚集程度较高，不同类样本之间没有重叠，具有明显的区分度，说明笔者所提特征类别可分性较强。其中，外圈故障的样本聚集度最高，正常状态的样本与其他类样本距离最远，这与从子网络平均度特征图中得出的结论是一致的。

图10 轴承PCA降维后的特征分布图

图11 现有网络拓扑特征的降维结果

现有的复杂网络方法大多从时域出发建模，且提取网络的1个拓扑特征参数来代表整个网络，如平均路径长度、聚类系数和平均度，这些特征是在全网的基础上计算的，对网络内部的局部变化不敏感，不能反映网络的微观特性。提取网络模型中现有的这3类特征，并进行相同的降维可视化处理，图11为滚动轴承4种状态下的平均路径长度、聚类系数和度经PCA降维后的结果。由图可以看出，现有网络拓扑特征对滚动轴承不同类样本的区分性较差，除正常状态与其他状态有明显差别外，3种故障互相交叉，难以准确区分。因此，与笔者所提特征相比，现有的网络拓扑特征类别可分性差，无法将其应用于后续的诊断和识别。

类别可分性测度是一种基于距离的特征评价函数，定义为样本中类内散度与类间散度的比值，可以评价一个特征子集的好坏程度，它的值越小，说明类间的可分性越好。相对于相同的分类器来说，好的类间可分性能够使分类器的识别率得到显著提高；而较为混杂、互相交叉的特征信息会使分类器的模式识别变得非常困难。下面将平均路径长度、聚类系数和度一起作为已有网络拓扑特征向量，与笔者所提子网络平均度特征(降到3维)从类别可分性测度的角度进行定量对比分析，对比结果如表2所示。由表2可以看出，本研究特征的类别可分性测度小于已有特征的类别可分性测度，说明本研究的特征在类别可分性方面优于已有网络拓扑特征，与上面定性分析结果一致。

表2 不同特征的类别可分性测度

2.2.2 识别结果

图12 轴承分类结果图

为验证子网络平均度特征在滚动轴承故障诊断中的效果，采用径向基函数(radial basis function，简称RBF)神经网络分类器[14]进行分类试验，每种状态选10个训练样本，10个检验样本，则训练样本共有40个，检验样本共有40个。对于以上4类40个训练样本，利用上述方法产生40个16维的特征向量。将40个子网络平均度特征利用RBF神经网络进行训练分类，得到如图12所示的滚动轴承不同故障分类图，其中：第1类为滚动体故障；第2类为内圈故障；第3类为外圈故障；第4类为正常。将笔者提出的子网络平均度特征输入RBF神经网络，识别正确率可达到100%。

时域特征参数由于计算简单、物理意义明确，很早就被应用于各种机械的故障检测和状态分析。本研究将用到以下14种时域统计特征量：均值、标准差、方差、偏斜度、峭度、峰峰值、方根幅值、平均幅值、均方幅值、极值、波形指标、峰值指标、脉冲指标和裕度指标，这些时域特征参数构成表征轴承状态的特征向量与笔者所提特征在RBF识别正确率方面进行对比。同样，每种状态选10个训练样本，利用RBF神经网络作为分类器识别剩余的10组样本，识别结果如图13所示。由图可知，将时域统计参数输入RBF神经网络，识别准确率可以达到97.5%。由此可以看出，可分性较好的特征对后续的精准识别十分重要。

图13 轴承分类结果图

为了更加客观地比较识别结果，从每类故障数据集中随机选取10组作为训练样本，利用RBF神经网络作为分类器识别剩余的10组样本。上文提到的时域特征参数和本研究特征各自独立运行，表3中的识别结果为各算法在Matlab中独立运行10次后的准确率的平均值与方差。从识别结果来看，本研究特征识别正确率均值高、方差小，说明本研究特征不仅类别可分性好，而且比较稳定，对同一数据集的不同训练数据，识别准确率不会产生较大波动。

表3 采用不同特征的RBF识别结果

3 结束语

为克服现有复杂网络建模方法和常规网络拓扑特征的缺陷，从频域的角度构建了新的复杂网络模型，利用复杂网络分解提取对网络局部变化敏感的子网络平均度特征。研究并获得子网络平均度提取方法及流程，采用6节点网络模型对本研究所提特征进行对比分析，并将其应用到滚动轴承故障诊断。与常用的网络拓扑特征平均路径长度、度、聚类系数进行定性分析和定量对比，验证了所提特征的优越性。将本研究所提特征用于滚动轴承故障识别，其识别正确率的均值和方差优于时域统计参数。