不确定性陶瓷热防护系统的双随机动态理论*

黄 杰， 姚卫星， 陈 炎,3， 孔 斌,3

(1. 南京航空航天大学飞行器先进设计技术国防重点学科实验室 南京，210016)

(2. 南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

(3.中国航空工业集团公司成都飞机设计研究所 成都，610091)

引 言

高超声速飞行器如X-37B空天飞机在再入大气层阶段会受到巨大的气动加热作用[1-3]，为保证飞行器的安全性，需要在飞行器表面设计TPS[4-6]，其中陶瓷防热瓦是再入飞行器应用最广泛的防热结构，其通过SIP黏接于飞行器蒙皮。TPS除了在再入大气层阶段抵御外部气动加热外，还会受到各种动态机械载荷的作用，最典型的为防热瓦外表面的声压激励和来自蒙皮振动的机体基础激励[7]。防热瓦和SIP在机械载荷的作用下将产生动态应力，动态应力过大会导致SIP发生破坏，防热瓦将与飞行器蒙皮分离，高超声速飞行器将发生灾难性的事故。因此发，研究防热瓦和SIP的动态响应具有重要的学术和工程价值。

在以往的研究中，TPS的动态响应主要是通过试验方法进行研究。文献[8-9]研究了正弦激励和随机激励作用下防热瓦和SIP的动态响应。文献[10-11]研究了SIP非线性刚度特性和黏性效应对防热瓦和SIP动态响应的影响。除了以上试验研究方法以外，一些学者通过理论方法研究了防热瓦/SIP的动态特性。George等[12]提出了TPS在声压激励和机体加速度激励作用下的单自由度动态特性理论模型，将防热瓦视为刚性体的一个质量点，将SIP视为线性刚度的弹簧和阻尼单元，并且假设声压激励和机体加速度激励功率谱密度(power spectral density, 简称PSD)函数均为限带白噪声，最后通过理论解预测了TPS随机动态响应。以上试验及理论的方法对TPS动态响应进行了研究，但未考虑TPS参数的随机性对TPS动态特性的影响，即未进行TPS动态特性的不确定性分析；而防热瓦和SIP的刚度、质量及阻尼特性常常表现出明显的不确定性，不考虑其不确定性影响必然会造成TPS动态特性分析结果的不准确。

为了研究TPS不确定性动态特性以及SIP不确定性动强度问题，笔者将防热瓦视为刚性体的质量点，将SIP简化为线性刚度的弹簧和阻尼单元，并且将防热瓦的质量及SIP的刚度和阻尼特性均考虑为随机参数，且服从正态分布，提出了在声压和机体加速度基础激励作用下的不确定TPS双随机动态理论模型，推导了防热瓦的加速度响应以及SIP动态应力响应的概率分布，研究了响应均值对随机参数的灵敏度，最后对比了所提出的理论模型的解与Monte Carlo数值解，验证了本研究不确定理论模型的正确性与分析精度。

1 热防护系统振动环境

笔者研究TPS的动态响应，根据文献[7]可知TPS承受的外部动态激励包括防热瓦外表面声压激励和来自蒙皮振动的机体基础激励，且这两种激励均为随机载荷，如图1所示。防热瓦外表面的声压激励来自于湍流边界层，其PSD函数通常为限带白噪声[13]。机体基础激励来自于发动机传递的荷载及非定常气动力引起的机体结构振动，且在试验中通常测量蒙皮的加速度信号。机体加速度基础激励的PSD函数通常为阶梯谱，图2给出了典型的谱型。在外部激励已知后，TPS的动态响应分析实际上为随机振动分析。

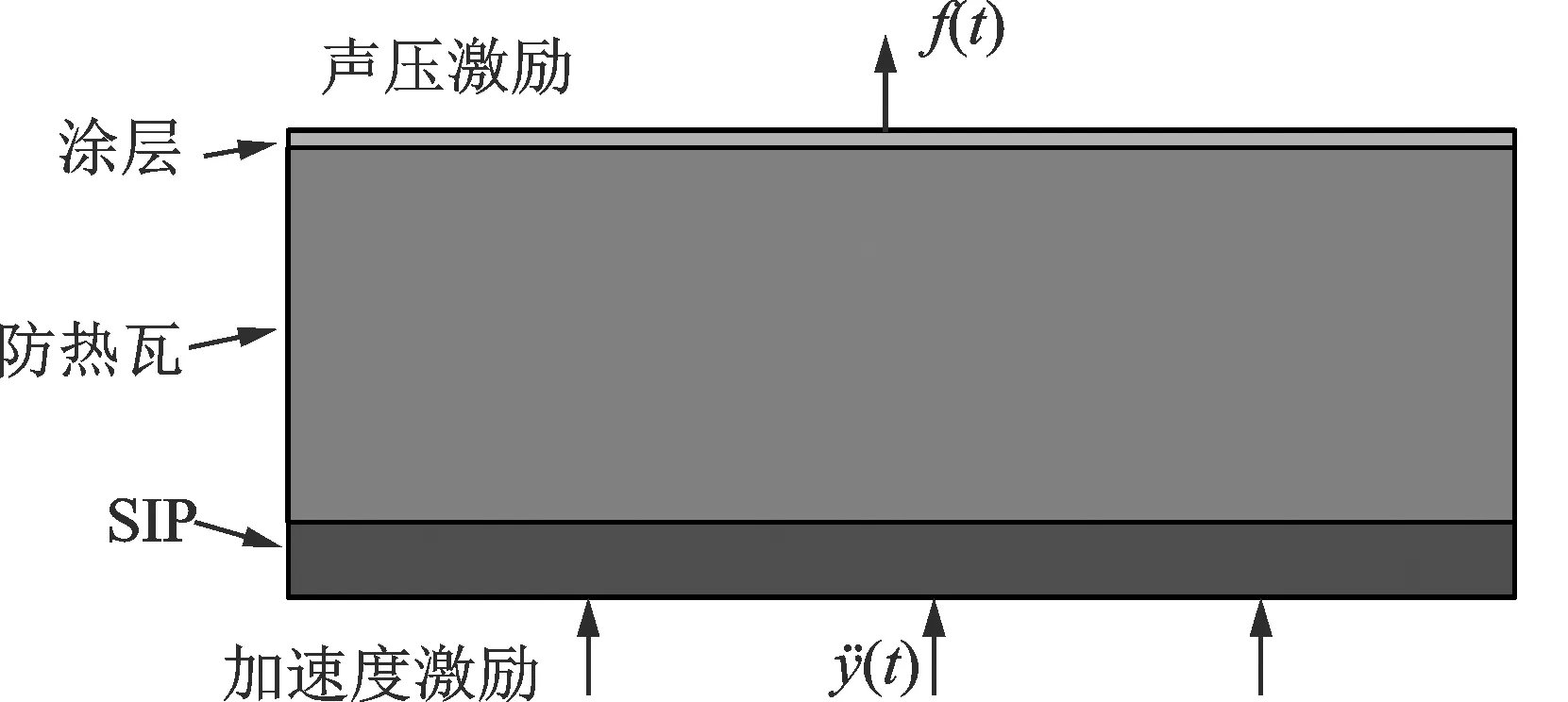
图1 TPS动态载荷来源

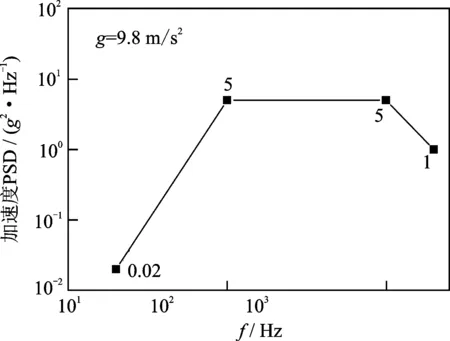
图2 典型基础加速度PSD函数

2 热防护系统动态理论模型

由于SIP刚度远小于防热瓦刚度[8-11]，故在建立TPS动力学理论模型时将防热瓦简化为刚性体，而将SIP简化为弹性体，构成了单自由度系统。SIP在不同环境下具有线性与非线性弹性本构，笔者仅考虑SIP的线弹性本构。由于TPS尺寸较小，宽度大概在50～200mm之间，可近似认为防热瓦外表面的声压激励均匀分布，机体对TPS底部的加速度激励也是均匀的。在建立TPS非线性动力学理论模型时作如下假设：

1) 系统进行平稳随机振动，且激励服从Gauss随机过程；

2) 将防热瓦简化为质量点以描述防热瓦的惯性力；

3) 将SIP简化为质量点、线性弹簧和阻尼器，分别描述SIP的惯性力、弹性力和阻尼力；

4) 声压激励和加速度基础激励均匀地作用于防热瓦外表面和TPS底部。

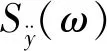
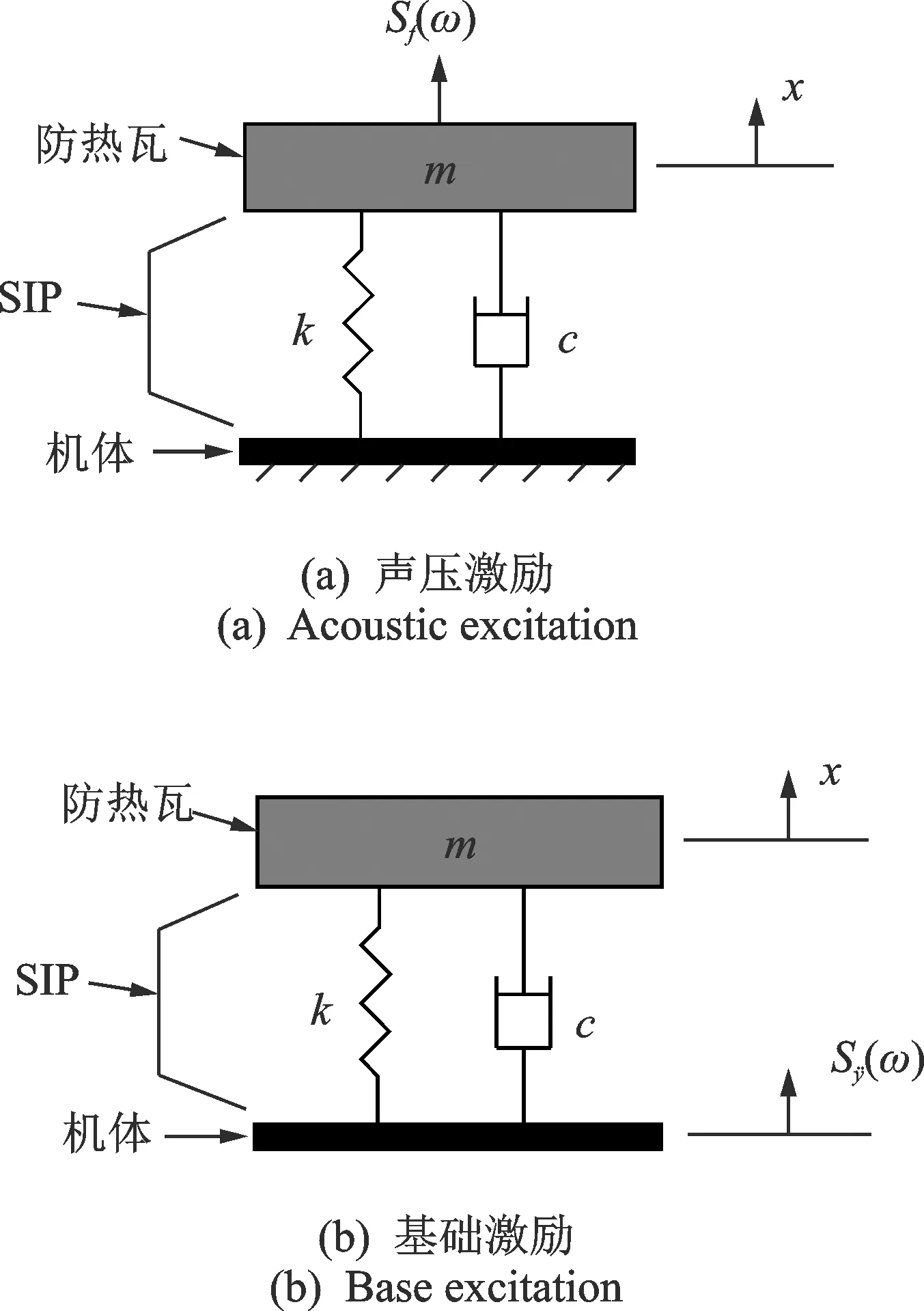
图3 TPS动态理论模型

由以上假设可得到在声压激励和加速度基础激励作用下的TPS单自由度系统运动方程分别为

(1)

(2)

3 热防护系统不确定性动态分析

(3)

(4)

第k个随机参数ηk和响应uk可分解为均值与零均值随机分量

(5)

(6)

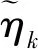
(7)

其中：m=3,为TPS随机参数的个数。

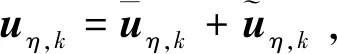
(8)

响应的协方差函数可以表示为

(9)

将式(8)带入式(9)可得

(10)

考虑式(5)，则式(10)可改写为

(11)

由式(11)可知，响应的协方差函数可由TPS随机参数的协方差函数Cov(ηk,ηq)来表达

Cov(ηk,ηq)=ρkqσηkσηq

(12)

其中：ρkq为随机参数ηk和ηq之间的相关系数；σηk和σηq为随机参数的标准差。

利用式(12)，将式(11)写成矩阵的形式,得

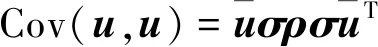
(13)

(14)

(15)

假设TPS随机参数相互独立

(16)

由式(13)和式(16)可得随机参数相互独立时的响应协方差函数为

(17)

针对某一响应v，式(17)可以简化为

(18)

针对第k个随机参数单独作用的情况，式(18)可以简化为

(19)

响应的变异系数可通过其均值和协方差求得

(20)

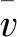
(21)

4 热防护系统动态响应均值

(22)

令外载荷F(t)=eiωt和位移响应z(t)=H(ω)eiωt，并将其代入式(22)即可得系统的位移频率响应函数H(ω)

(23)

根据随机振动理论可得防热瓦的位移、速度及加速度PSD响应函数为

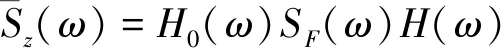
(24)

(25)

(26)

将以上响应的PSD函数在频域下积分，即可得防热瓦的位移、速度和加速度均方值

(27)

(28)

(29)

(30)

(31)

其中：S为SIP面积。

5 算例参数

笔者进行了不确定性陶瓷热防护系统的双随机动态响应算例分析，其中防热瓦和SIP的宽度W、厚度h、密度ρ及结构阻尼系数g如表1所示。SIP的弹性模量为1.46MPa，根据SIP的厚度和面积计算得到弹簧刚度系数k为6.317 3kN/mm，根据防热瓦和SIP的密度和体积计算得到TPS的总质量m为0.578 8kg。此外声压激励的PSD函数Sf(ω)为限带白噪声，其在频域范围20～2 000Hz内保持400N2/Hz不变，本研究采用图2中机体加速度基础激励的PSD函数。

表1 TPS参数

由于图3中的阻尼特性是由黏性阻尼系数c表征的，故需将结构阻尼系数g转换为黏性阻尼系数c，其表达式为

c=gmωn

(32)

其中：ωn为单自由度系统的固有频率。

根据式(32)计算得到SIP的黏性阻尼系数c为76.487 3(N·s)/m。

6 响应均值的灵敏度分析

进行不确定性TPS动态分析之前需要进行式(21)中的响应均值对随机参数的灵敏度分析。系统质量、刚度系数和阻尼系数的均值及变异系数如表2所示，其中所有随机参数的变异系数均为0.03。

表2 随机参数的均值和变异系数

Tab.2 The mean values and variation coefficients of random parameters

ηkm/kgk/(kN·mm-1)c/((N·s)·m-1) ηk0.578 86.317 376.487 3η′k0.030 00.030 00.030 0

笔者采用差分法进行灵敏度分析，差分格式为

(33)

其中：Δηk为差分步长。

式(33)采用具有2阶精度的中心差分格式代替原有的偏导数，需要确定合适的差分步长Δηk以保证差分精度。

本研究的差分步长表示为随机参数标准差的倍数关系，如式(34)所示，其中系数λ取0.1，1和10，进行了3种不同差分步长下响应均值对随机参数的灵敏度分析

(34)

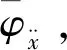
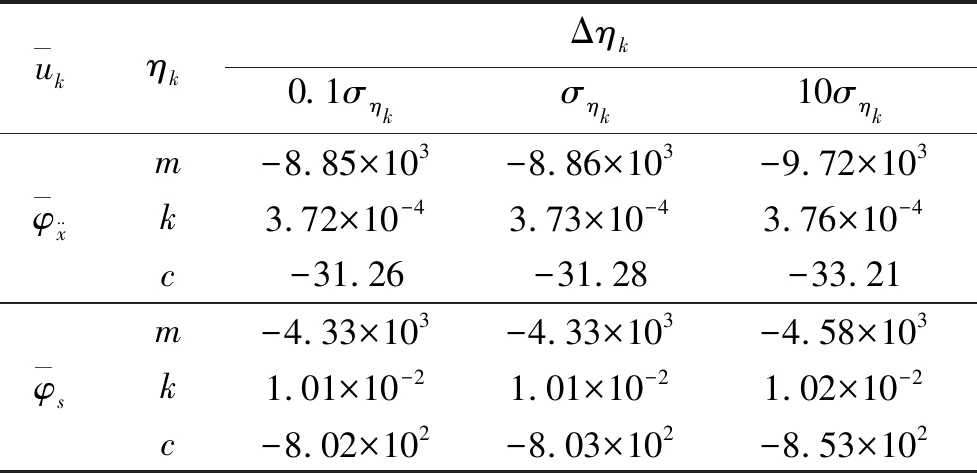
表3 声压激励下的灵敏度分析结果

表4 基础激励下的灵敏度分析结果

7 响应概率分布及Monte Carlo数值验证

利用表3和表4中差分步长Δηk=σηk对应的灵敏度分析结果即可进行防热瓦/SIP系统的响应概率分布分析。此外，为了验证本研究的理论分析结果的合理性，进行了Monte Carlo数值计算，其分析流程如图4所示，具体步骤为：

1) 筛选随机变量(随机参数)，并指定随机变量的概率分布；

2) 设置模拟的最大仿真次数N(本研究设置为104次)；

3) 生成均匀分布的随机数序列，并将其转化为相应的随机变量值；

4) 调用计算程序对当前随机参数值的响应进行计算；

5) 重复步骤3～5，直至模拟最大次数N或均值和标准差收敛，结束循环；

6) 对响应值进行统计分析(均值、标准差、范围和分布形状)。

图4 Monte Carlo数值分析流程

利用以上灵敏度分析结果和式(19)，进行了单个随机参数情况下的防热瓦/SIP系统的响应概率分布分析。表5和表6分别列出了声压激励和加速度基础激励作用下防热瓦加速度和SIP应力的均值和标准差分析结果，其中A代表理论分析结果，B代表Monte Carlo数值计算结果。可以发现响应的均值和标准差的理论分析结果与Monte Carlo数值计算结果吻合得很好，相对误差控制在1.5%以内。

表5 声压激励情况下单随机参数的概率分析结果

Tab.5 The probability analysis results under acoustic excitation

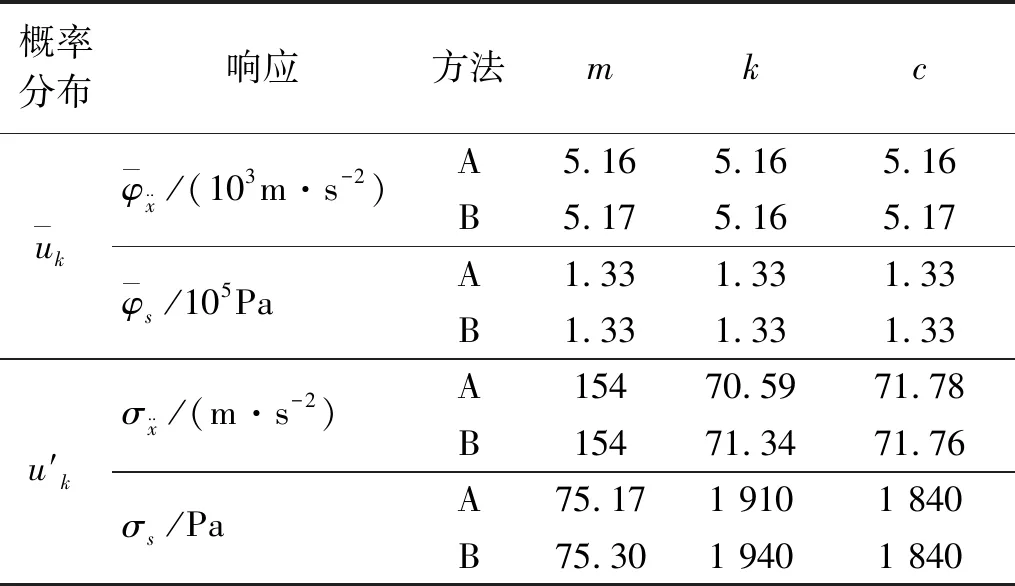
概率分布响应方法mkc uk φ¨x/(103m·s-2)A5.165.165.16B5.175.165.17 φs/105PaA1.331.331.33B1.331.331.33u′kσ¨x/(m·s-2)A15470.5971.78B15471.3471.76σs/PaA75.171 9101 840B75.301 9401 840

表6 基础激励情况下单随机参数的概率分析结果

Tab.6 The probability analysis results under base excitation for single random parameter

概率分布响应方法mkc uk φ¨x/(103m·s-2)A3.153.153.15B3.153.143.15 φs/104PaA8.098.098.09B8.098.108.09u′kσ¨x/(m·s-2)A0.022 547.2347.23B0.022 547.1847.53σs/103PaA2.431.211.21B2.431.211.22

图5和图6分别为Monte Carlo数值方法计算得到的在声压激励和加速度基础激励作用下防热瓦的加速度以及SIP应力的概率分布图。从图中可观察到，所有响应的概率分析均趋近于正态分布，这是由于本研究的随机参数和载荷均服从正态分布，且防热瓦/SIP为线性系统，响应理论上必定服从正态分布。

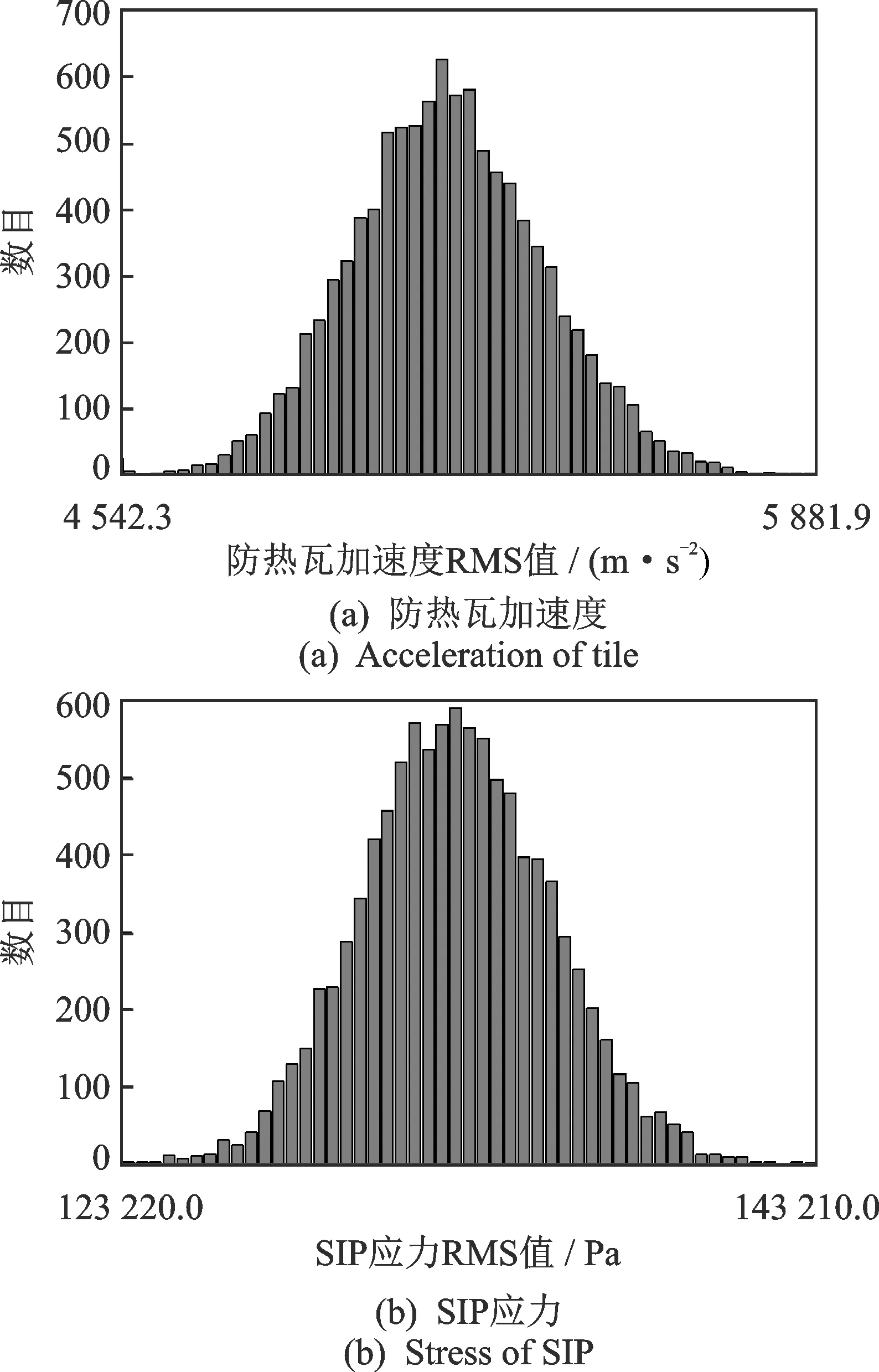
图5 声压激励下Monte Carlo数值模拟响应概率分布

图6 基础激励下Monte Carlo数值模拟响应概率分布

根据式(18)和式(19)，考虑所有随机参数的情况下，响应的方差为单个随机参数情况下求得的方差之和。表7列出了考虑所有随机参数时在声压激励和加速度基础激励作用下响应的均值和标准差分析结果，其中A代表理论分析结果，B代表Monte Carlo数值计算结果。可以发现防热瓦的加速度响应以及SIP应力响应的均值和标准差的理论分析结果与Monte Carlo数值计算结果吻合得很好，相对误差控制在1.5%以内。

表7 所有随机参数情况下的概率分析结果

Tab.7 The probability analysis results for all random parameters

概率分布响应声压/基础数值 uk φ¨x1/(103m·s-2)AB5.16/3.155.17/3.15 φs/104PaAB13.3/8.0913.3/8.10u′kφ¨x1/(m·s-2)AB184/66.79185/65.82σs/103PaAB2.66/2.972.65/2.93

8 结 论

1) 将防热瓦假设为刚性体，简化为质量点，将SIP假设为弹性体，简化为线性弹簧和阻尼单元，假设以上质量点、刚度和阻尼服从正态分布，提出了在外界随机激励作用下的不确定性TPS双随机动态理论模型。

2) 采用摄动法研究了防热瓦加速度响应以及SIP应力响应的概率分布，得出其关键问题是进行响应均值对TPS随机参数的灵敏度分析。

3) 进行了算例分析，本研究理论方法获得的响应概率分布和Monte Carlo数值计算结果吻合得很好，从而验证了所提出的不确定性TPS双随机动态理论模型的正确和分析精度。

4) 本研究工作为防热瓦不确定性加速度特性、SIP不确定性动强度和TPS不确定性动态完整性分析提供了理论依据。