随机行走激励楼盖振动加速度反应谱*

张志强， 周 晨, 张晓峰， 李爱群

(1. 东南大学土木工程学院 南京，210096)

(2. 东南大学混凝土及预应力混凝土结构教育部重点实验室 南京，210096)

(3. 美国堪萨斯州立大学建筑工程与施工学系 堪萨斯州，66506)

(4. 北京建筑大学土木与交通工程学院 北京，100044)

引 言

随着科学技术的发展，建筑越来越往大跨度低阻尼方向发展，随之产生的振动舒适度问题在工程设计中愈加显著[1]。作为结构动力分析的主要方法之一，时域分析法主要研究承受复杂荷载作用下结构在时间历程上表现的动力响应。由于激励作用的步行荷载具有随机性，为了准确预测步行荷载作用下楼盖的振动响应，需有足够数量且精确的步行荷载样本曲线对结构人致振动响应进行仿真分析，然后统计并处理样本分析结果。在大量分析数据基础上最终建立楼盖振动加速度反应谱曲线，既可以避免以往单次时程分析产生计算结果误差，也可以提高计算效率。

Brownjohn等[2]从理论上提出并完整地建立人行桥人致振动谱分析方法，假设等自重的人群过桥时沿桥长均匀分布，采用抖振分析方法推导人行桥面任意位置处人致振动竖向位移响应谱。Ricciardelli[3]通过试验研究创建了行人步行力功率谱，在此基础上结合随机振动理论，推导了均布行人步行力作用下的人行桥模态峰值加速度。钱晓斌[4]大量计算分析包括简支、多跨和H型等多种形式的结构，根据海量计算数据构造了均方根加速度响应谱。宋志刚等[5]基于实测的有代表性的落步曲线，进行了大量的时程分析计算，分析最大加速度响应谱基于振型阶数、阻尼、跨度和边界条件下结构振动的敏感性，从而得出加速度响应谱的包络曲线。韩小雷等[6]分析4～14 Hz范围的楼盖，定义行人随机开始时间、匀速行走、直线路线、体重服从N(0.7，0.145)(kN)正态分布的随机数据等，假定这些计算参数分布特性，生成随机步行荷载计算了人群行走下楼盖的振动响应，最终拟合了反应谱曲线。陈隽等[7]基于61人次2 204条实测的步行荷载曲线，提出了计算单人步行竖向荷载作用下大跨度楼盖加速度均方根响应的反应谱，并基于楼盖频率与振动幅值双控原则，对计算反应谱进行了拟合简化，提出了1～10 Hz 频率范围的设计使用楼盖均方根加速度响应计算表达式[8]。

笔者精确模拟单人的随机行走工况，考虑了人行走特点[9]，使用移动步行力法激励结构，通过蒙特卡罗法生成海量的考虑步行参数概率分布的随机单人步行荷载曲线，计算试验楼盖的加速度均方根响应的反应谱曲线。在此基础上拟合出了10 Hz频率范围以内楼盖的标准反应谱公式，形成楼盖振动响应的标准反应谱计算方法，比较计算理论值与实测楼盖响应值差异，联系实际工程验证反应谱计算方法的适用性。

1 随机步行荷载仿真数据生成

1.1 单人步行荷载

单人在正常行走时可用步频、步幅、双脚重叠时间等参数来描述行走特征。崔常慧[10]从试验的角度出发，研究了单人步行荷载的影响参数及荷载模型，如图1布置步行测力板，通过压力测力板测试青年个体行走时产生的步行荷载，总共测试20 000余组数据，对自由行走工况下利用复步荷载拓展获得连续步行荷载曲线表示

(1)

其中：fp为行人步频(Hz)；G为行人的体重(N)；DLF为第i阶谐波分量的动载因子(dynamic load factor，简称DLF)；φi为第i阶简谐荷载分量的相位角；DLFsubi为竖向第i阶次谐波分量的动载因子；φsubi为第i阶次谐波分量的相位角；n1，n2为所选取的主谐波和次谐波的阶数。

图1 单人行走测试图

公式参数选择按照表1取值。其中：体重试验分析根据实际体重取值；步频为1.886 Hz。

1.2 单人步行路线设计

表1 单人步行荷载试验参数取值

单人行走路径参考社会力模型[11](social force model，简称SFM)建模思路。行人基于现实需求，在周围环境和个人目的驱使下，综合判断评估处理信息，选取合适的路径行动。单人行走时受自身驱动力及边界排斥作用力影响，行走的位移可利用微分方程求解，由此得出行走路径。自驱动力源于行人受预期目标吸引，同时又受到在运动过程中偏离本身期望运动方向速度的作用而产生的力。边界排斥力通过计算边界上到行人中心点最短距离的点，再通过公式计算得到[12]。经计算，单人行走的路径表现为行人基本沿着直线行走，走到边界掉头，根据重新定义的新的行走目标继续行走，如此来回。假设质量为mi的行人受到力的推动，得出行人所受力的微分方程式(2)，加速度为位移的两阶导数，结合时间步求解可以得到下一个时间步行人i的位置

(2)

计算各个时刻行人的空间位置，分析行人随机行走引起的空间分布随机性对结构振动响应的影响。

1.3 Matlab编程实现单人随机行走过程

单人随机行走需模拟实际移动行走的形态，不仅是频率、相位，还包括行走位置、行走方向等。笔者采用Matlab软件编程生成随机步行荷载加载至结构计算结构响应。

根据SAP2000有限元软件划分网格的特点，以及国内相关规范对我国成年人尺寸做的统计，将行人简化长轴约为0.4 m、短轴约为 0.2 m的椭圆体[13]，划分成0.4m×0.4m的网格。计算的行走路线将行人荷载加载作用位置投射至最近的网格点。单人行走单步作用点都落足于图2楼盖各个编点处，行人随机行走整个过程即为楼盖各个编号点的受力过程，整个随机行走即是楼盖各点不同时间的受力，统计每个编号点在整个行走过程总时间段的时程荷载曲线，形成M×N人行荷载矩阵。程序编程思路[14-15]如图3所示。

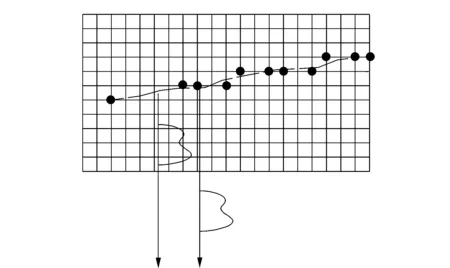
图2 行人行走路线及楼盖受力点示意图

对于任意频率的结构，模拟楼盖振动响应分析，样本的置信度为0.95，对于指定误差ε=0.005 5，最终模拟抽样的次数n取值为1 000。

2 随机步行荷载激励下楼盖反应谱曲线生成

人行走作用下的矩形薄板，在沿长度(宽度)方向走动引起的振动微分方程[16]可以表达为

(3)

δ(·)函数定义为

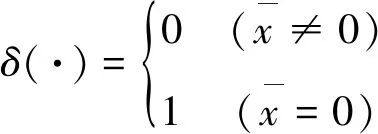
(4)

(5)

其中：te为人的脚部跟楼地面接触的时间：ts为步频的倒数；f(τ)为单步落足曲线。

由板壳振动理论公式得出，第j振型可表达为

φj(x,y)=pj(x)gj(y)

(6)

其中：pj(x)，gj(y)分别为[0,a]，[0,b]这两个区间内x与y方向的振型，在其定义范围内这两个方向的振型的最大值为1。

考虑在其中的一个方向上走动，薄板的强迫振动方程如式(3)所示，进行振型分解，得到

(7)

Fjr为Fj(t)的最大绝对值，即Fjr=max|Fj(t)|。 式(7)可以表示为

(8)

将微分方程定义的振动系统转化为标准激振系统

(9)

将Sjmax(ω)定义为标准激励系统下的加速度响应的最大绝对值

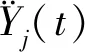
3 标准反应谱生成

3.1 反应谱曲线计算

图4 2.2 Hz随机行走激励楼盖加速度均方根反应谱曲线

使用SAP2000建立四边简支的广义单自由度试验楼盖。建立楼盖模型，楼盖的主振型频率范围为1～10 Hz，不同振型的楼盖以0.1 Hz为增量依次递增。在楼盖上施加随机单人步行荷载仿真曲线，计算主振型从1～10 Hz楼盖结构的加速度响应值，得出1条反应谱曲线。图4为某次单人随机行走的反应谱曲线，频率为2.2 Hz，阻尼比为0.01，图中标出步频及其倍频的位置。分析阻尼比为0.01的结构在1 000次随机步行荷载时的加速度时程响应。由于人在结构上的耐受极限与时长有关，持续时间越长相应的耐受极限也会降低，因此考虑采用均方根(root mean square,简称RMS)加速度作为代表值可以兼顾时间这一变量，最终确定将10s的均方根值作为结构响应分析的代表值。图5为某测试者2.2 Hz随机步行荷载得到的0.01～0.05阻尼比下10 s加速度均方根值反应谱曲线。1 000次随机单人步行荷载10s加速度均方根值的反应谱曲线如图6所示，图7为其外包络曲线。

图5 2.2 Hz随机行走激励不同阻尼比反应谱曲线

图6 10 s均方根加速度反应谱图

图7 10 s均方根加速度反应谱外包络曲线

3.2 反应谱曲线形式的确定

由于每个人行走的频率、相位与路线均有差异，因此每一个测试样本的加速度反应谱曲线均不同，而取所有样本的加速度反应谱曲线的外包络线可以反映出结构针对测试者施加所有工况的最大响应。

笔者研究的随机步行荷载考虑频率、相位、路线的随机性生成大量移动的随机步行荷载曲线。本研究计算1 000条响应谱曲线的包络曲线见图7，考虑到计算方便以及曲线模型的直观性，采用反应谱的模型包含上升段、水平平台段以及下降段。从1 000条均方根响应谱曲线可看出：结构自振主频率在0.7～1.5 Hz区间内，曲线为直线上升段；1.5～2.5 Hz区间，均方根加速度曲线在平台附近上下波动，整体趋于平稳；2.5～3 Hz为直线下降段；3～10 Hz曲线是一个下降至平稳的趋势。笔者计算得出的基于随机步行荷载下结构的加速度反应谱如图8所示。

图8 单人随机行走激励的10 s均方根加速度反应谱曲线模型

3.3 反应谱曲线计算

根据式(8)，对计算的均方根响应值进行归一化模拟时，根据归一化的均方根加速度响应谱曲线按照图8的3段曲线形式反应谱模型确定参数取值。

3.3.1 平台参数的确定

图9 基于极值概率分布的平台段aRMS(ξ)取值统计特性

根据已经计算得出的平台段内加速度幅值的概率分布特性，可以求解并确定平台段的设计值。统计1.5～2.5 Hz区间内10s均方根加速度的概率分布，按从小到大分为若干区间，对每个区间频数进行统计，对统计结果进行概率密度曲线的拟合。图9为阻尼比0.01～0.05结构平台段的统计特性，其幅值符合最大Ⅰ型极值分布，通过数值求解法计算出95%和75%保证率下的加速度均方根值分位点。

分析不同结构阻尼比ξ与均方根分位点的关系，最终得到aRMS的计算式及aRMS(ξ)与阻尼比ξ的拟合曲线，如表2所示。

3.3.2 下降段参数的确定

曲线下降段基于平台段的数值aRMS(ξ)，采用的函数形式为

α(f,ξ)=aRMS(ξ)αfβ

(12)

其中：f为结构频率。

各阻尼比的结构统一取值如下

aRMS=0.6aRMS(ξ) (3/f)1.226

(13)

表2 基于保证率加速度均方根值的的分位点取值及aRMS(ξ)拟合曲线

Tab.2 Point value of RMS of acceleration based on the guarantee rate and fitted curve ofaRMS(ξ)m/s2

阻尼比95%保证率加速度均方根值分位点75%保证率加速度均方根值分位点0.013.892.530.022.761.930.032.171.580.041.701.350.051.531.22拟合曲线aRMS (ξ)=0.286 2ξ-0.569 1aRMS (ξ)=0.326 9ξ-0.446 4

3.4 标准反应谱曲线表达式

给出基于保证率的设计反应谱见式(14)，对应如图10所示，平台段取值按表2计算。其中：95%保证率下的aRMS(ξ)= 0.286 2ξ-0.569 1；75%保证率下的aRMS(ξ)=0.326 9ξ-0.446 4。

(14)

3.5 基于保证率的反应谱曲线

笔者通过模拟出大量随机人群行走的结构响应反应谱曲线，分别基于95%和75%的保证率求得平台段参数aRMS的取值。基于模型曲线的假设与研究方法，所给出的反应谱曲线模型在95%保证率下与一些工程楼盖实测结果相吻合，能较好地预测楼盖响应。图10中实心点为一些实际工程的实测结果。笔者将95%的保证率计算得出的平台参数应用于标准反应谱曲线模型。

图10 反应谱曲线模型与实测值的比较

3.6 标准反应谱曲线影响参数

反应谱曲线影响参数取值，笔者总结相关研究的结论[4-8]列出如下：a.不同边界条件反应谱曲线数值影响程度较小，采用四边简支边界的结构计算所得的标准反应谱，可以简化结构计算；b.跨度对结构响应的影响通过跨度调整系数，经计算，对于阻尼比0.01结构，η=1+0.06(L-8)，对于阻尼比0.05结构,η=1+0.024(L-8)，L为楼盖长边跨度，其他阻尼比按照插值计算；c.阻尼比的影响在反应谱曲线公式中进行调整。

3.7 标准反应谱法计算步骤

笔者运用反应谱方法计算楼盖竖向加速度响应，其步骤如下。

1) 采用有限元方法或者实测方法计算得出楼盖的竖向主频率fi及竖向主振型参与质量Mi，其中下标i表示楼盖第i阶振型。

2) 确定结构阻尼比后按照式(14)计算每阶竖向主振型对应的单人随机行走作用下10s均方根加速度反应谱值。

3) 按下式计算第i阶振型对应的10 s均方根加速度响应

(15)

其中：φi,1为响应验算点第i阶振型值；φi,2为行走路线上对应的第i阶振型值；G为行人体重；Mi为对应主振型模态质量；η为楼盖跨度调整系数。

4) 第i阶振型对应的峰值加速度[7]为

ai,max=2ai,RMS

(16)

5) 峰值加速度响应按下式进行计算

(17)

4 工程应用评估

4.1 现浇试验楼盖实测案例1

试验楼盖平面尺寸为5 000 mm×8 000 mm，混凝土等级为C30。相应前3阶模态数值如表3所示。结构阻尼比无人时为0.01。将有限元模型与楼盖结构实测的主振型频率对比，数据契合，说明有限元模型模拟可靠，可做进一步研究分析。

表3 Sap2000模态分析结果

经研究，1阶主振型为4.6 Hz。跨中最大响应只由第1阶主振型控制，采用式(15)给定公式计算，楼盖主振型的模态质量经有限元计算为6 551 kg，修正计算跨度，最大响应处振型值φi,1为1，行走路线经过结构最大响应处，行走路线上对应的第i阶振型值φi,2最大也为1。单人行走，结构阻尼比取0.01。

采用传统有限元方法数值模拟，在结构主振型最大响应区域布置移动的固定频率荷载，行走工况包括1.5 Hz(引起结构3阶共振)、2.0 Hz(对照工况)、2.3 Hz(引起结构2阶共振)。

楼盖试验测试时，单人按照1.5，2.0和2.3 Hz的节拍器在楼盖上行走，测试中发现楼盖跨中的振动响应最大。测试人员体重约为620 N，在试验楼盖纵向来回行走，1次测试时间为1 min，总共测试20次。每次数据取最大响应值，最终测试值取20次最大响应值的平均值。

计算结果如表4所示，有限元模拟时，1.5和2.3 Hz分别引起结构的3阶与2阶共振，结构响应计算值均比较大，其中2.3 Hz荷载工况下，跨中最大响应值达到293.5 mm/s2。测试行走时，行人按照2.3 Hz节拍行走的结构响应测试在跨中处响应值最大，达到245.0 mm/s2，不过1.5 Hz行走的行人并未激发结构的3阶共振，1.5Hz行走有限元模拟值与实测误差较大。使用反应谱法求解由于已经考虑最不利，最大响应值为268.7 mm/s2，与测试值误差仅为9.6%。从试验楼盖的实测数据显示，笔者给出的反应谱曲线能较好地反映楼盖的振动响应，也说明本研究给出的响应谱曲线模型有效可靠。

表4 各工况下不同计算方法与试验结果对比

Tab.4 Comparison between the theoretical values of different calculation methods with test results under different working conditions

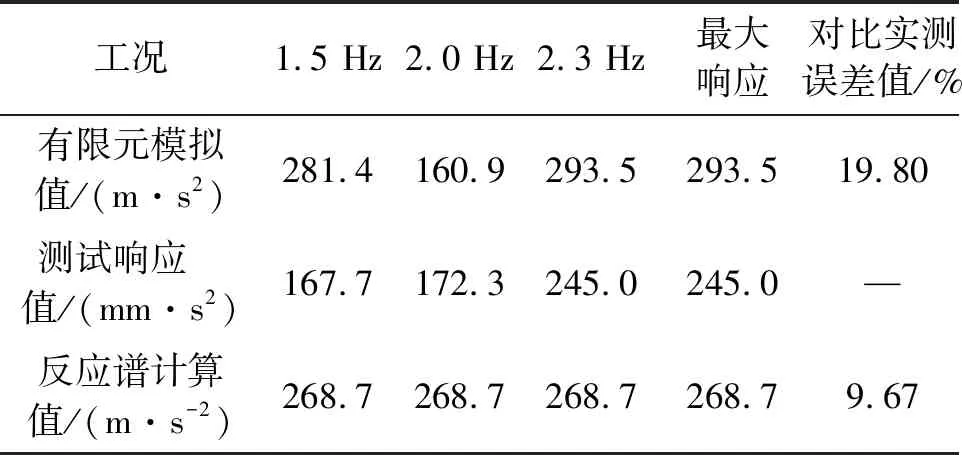
工况1.5 Hz2.0 Hz2.3 Hz最大响应对比实测误差值/%有限元模拟值/(m·s2)281.4160.9293.5293.519.80测试响应 值/(mm·s2)167.7172.3245.0245.0—反应谱计算值/(m·s-2)268.7268.7268.7268.7 9.67

误差=(计算值-实测值)/实测值

4.2 大跨楼盖现场实测案例2

以闵行生态博物馆大跨悬挑楼盖为例，将现场最不利工况测试的响应结果与有限元模拟的数值结果、反应谱方法计算的理论值进行对比，分析反应谱法与实际工程结果的契合程度。

钢梁组合楼盖承担楼面荷载，楼盖悬挑长度为16 m，经计算，楼面竖向主振型分别为3.4和4.4 Hz。楼盖主振型实测与理论数值及相应楼盖阻尼比如表5所示。图11中有限元模拟的前2阶振型与实测结果十分接近，振型形状十分吻合，楼盖计算阻尼比取0.025。

表5 2楼楼盖前2阶竖向频率计算理论值与实测值对比

Tab.5 Comparison between calculated value and measured value of the second floor′s vertical frequency of the first 2 orders

竖向振型阶数竖向频率/Hz理论值实测值误差/%实测阻尼比/%13.383.370.302.5024.304.453.492.47

现场实测是单人来回行走，行走区域集中在楼盖的跨中部位，即图11中2处部位。楼盖的前2阶主振型分别为3.4与4.5 Hz。经理论计算与实测发现，行人以1.7与2.2 Hz行走时，楼盖的振动响应较大，行走激励激发楼盖前2阶振型的2阶共振。经测试，最大响应主要集中在第1、第2阶振型的最大振幅处，即图11中的1和2处。测试时行人听从节拍器的拍声行走，在楼盖上布置传感器测试结构响应值。采用传统有限元方法数值模拟，在楼盖的跨中区域布置移动的固定频率荷载，荷载频率与测试工况相同。表6中分别给出楼盖结构1和2处1阶、2阶振型的加速度反应谱值，由式(17)可得结构峰值加速度响应与各个竖向主振型反应谱值相关。计算显示2处结构反应谱值要高于1处。

图11 楼盖动力特性测试测点编号图

在实测中，当行人以1.7 Hz节拍行走时1处响应最大，当行人以2.2 Hz节拍行走时2处响应最大，这个测试结果与有限元计算出来的模拟结果吻合。2.2 Hz行走时2处的响应值略高于1.7 Hz行走时1处，测试结果、有限元模拟、反应谱计算都能得出这个结论。考虑2处位于结构跨中，而1处位于边缘，因此工程分析中尤其需要考虑2.2 Hz行走产生的舒适度问题。这说明反应谱分析有助于得出引起结构较大响应的主振型以及最大响应处的位置，这对结构减振控制起到参考作用。两种不同方法计算最大响应值与实测峰值之间的误差分别为14.57%和5.98%，误差均很小，这也说明反应谱曲线法计算结构响应具有重要且可靠的参考价值。

表6 大跨楼盖反应谱法计算与有限元法及实测数值对比

Tab.6 Comparison between response spectrum method values with finite element method values and measured data

项目试验最不利工况测试值有限元最不利工况计算值反应谱峰值加速度响应1处结构响应值/(mm·s-2) 14.95(1.7 Hz工况)18.79(1.7 Hz工况)19.852处结构响应值/(mm·s-2) 21.40(2.2 Hz工况)24.52(2.2 Hz工况)22.68最大响应与实测误差/%—14.575.98

4.3 大跨楼盖现场实测案例3

武汉大学万林艺术博物馆建筑北侧为悬挑结构，最大悬挑长度约为41 m。建筑物东西外表面内侧各设置一榀悬挑钢桁架，桁架支承在1.2 m厚的型钢混凝土墙上。楼盖结构竖向1阶主振型(图12)理论值为3.01 Hz，实测振型为3 Hz，结构实测阻尼比为2.6%。

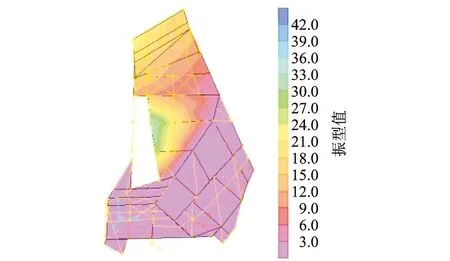
图12 楼盖结构主振型

行走范围布置在楼盖振动响应最大区域，如图13所示。荷载频率采用1.5 Hz(激发结构主振型)和2.0 Hz(参考工况)，行人听从节拍器的拍声行走，在楼盖上布置传感器测试结构响应值。采用传统有限元方法数值模拟，在楼盖的跨中区域布置移动的固定频率荷载，荷载频率与测试工况相同，在主振型最大振幅处布置拾振器测量加速度，同时采用反应谱法计算该点加速度响应值。

图13 楼盖上行人行走区域

从表7中可以看出，1.5 Hz步频荷载下结构响应高于2.0 Hz，行走激发结构的2阶共振，有限元模拟值与测试响应值吻合，同时有限元模拟与反应谱计算的结果均接近实测响应，反应谱方法计算有一定的可靠性。

表7 各工况下不同计算方法与试验结果对比

Tab.7 Comparison between theoretical values of different calculation methods with test results under different working conditions

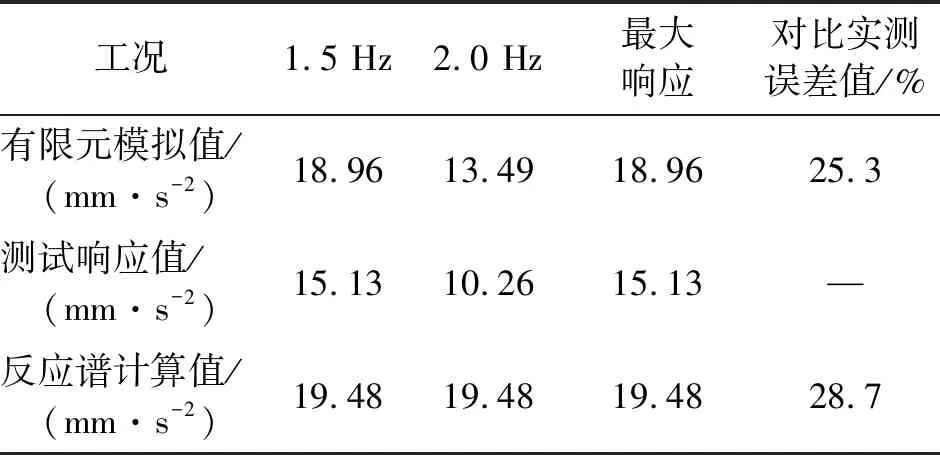
工况1.5 Hz2.0 Hz最大响应对比实测误差值/%有限元模拟值/(mm·s-2)18.9613.4918.9625.3测试响应值/(mm·s-2)15.1310.2615.13—反应谱计算值/(mm·s-2)19.4819.4819.4828.7

总结3个现场实测的工程案例，将单人行走的实测最大响应值与有限元模拟的行人荷载响应值、反应谱计算的振幅最大处响应值进行对比，结果见图14。采用反应谱计算的公式与有限元分析大致吻合，与实测响应误差基本在20%左右。加速度反应谱方法可以作为工程结构振动响应计算的参考方法。

图14 3个工程案例不同计算方法结构响应值对比

5 结束语

当实际工程中研究步行荷载下楼盖的振动响应时，反应谱计算方法可以较快及较精确地计算得出结构的最大响应位置及响应值，用于结构减振分析。笔者模拟行人随机行走时，采用蒙特卡罗法生成大量基于概率分布的移动随机步行荷载曲线，在此基础上计算得出楼盖标准加速度反应谱曲线模型。通过3个楼盖结构现场的实测案例，将研究的反应谱模型计算与有限元模拟计算、现场实测之间的结果进行对比，数值基本吻合，验证了反应谱计算方法的可靠有效。该反应谱计算方法应用于实际工程中，有助于获得引起结构较大响应的主振型以及最大响应的位置，对结构减振控制起到参考作用。同时反应谱方法计算值与实测数据误差较小，可供大跨混凝土楼盖振动舒适度的设计和结构振动评估应用。