一种小型全轴摆动喷管流场计算和性能分析*

2019-12-28尚永腾白涛涛

弹箭与制导学报 2019年4期

尚永腾，白涛涛

(中国空空导弹研究院，河南洛阳 471009)

0 引言

推力矢量控制(TVC)是未来先进战术导弹的必备技术之一，可大大提高导弹的机动速度和转弯能力[1]。目前TVC系统大致可分为摆动喷管致偏、阻流致偏和流体二次喷射致偏三类[1-2]。其中摆动喷管作为一种高效的TVC手段，在国内外得到了广泛的研究和应用[3]。

美国ATK公司对各种构型的摆动喷管进行了大量的仿真和试验[4]，其研制的球窝喷管在众多型号中得到应用。挪威Nammo公司对长尾管式的超音速分离线摆动喷管进行了研究[5-6]，其开发的代码能计算包含任意粒子组的二维和三维流场。国防科技大学的刘君等采用三维薄层近似N-S方程[7]，西北工业大学的杨玉新采用分区网格技术[8]，海军工程学院的周红梅等采用动网格[9]对潜入摆动喷管进行了数值模拟，分析了喷管摆动对性能的影响。西安现代控制技术研究所的刘宇涛对一种潜入球窝喷管进行了流场计算[10],从出口总压和入口速度分布的角度对比了两个摆角状态的流场变化。目前摆动喷管的研究多针对已在战略导弹上成熟应用的大型潜入喷管，而针对空空导弹等小直径战术导弹的小型、长尾管式的摆动喷管却鲜有报道。

文中提出一种长尾管式的小型全轴摆动喷管，采用CFD方法对不同条件和状态的一系列工况进行三维内流场数值模拟，分析摆动喷管的流场特性并评估各因素对喷管性能的影响。

1 物理模型及网格

1.1 物理模型

文中所述小型摆动喷管与长尾喷管结合，分为固定部分和摆动部分，两者中间为分离线，其结构如图1所示，在两组驱动杆的作用下可实现360°全向摆动，最大摆角为±10°。

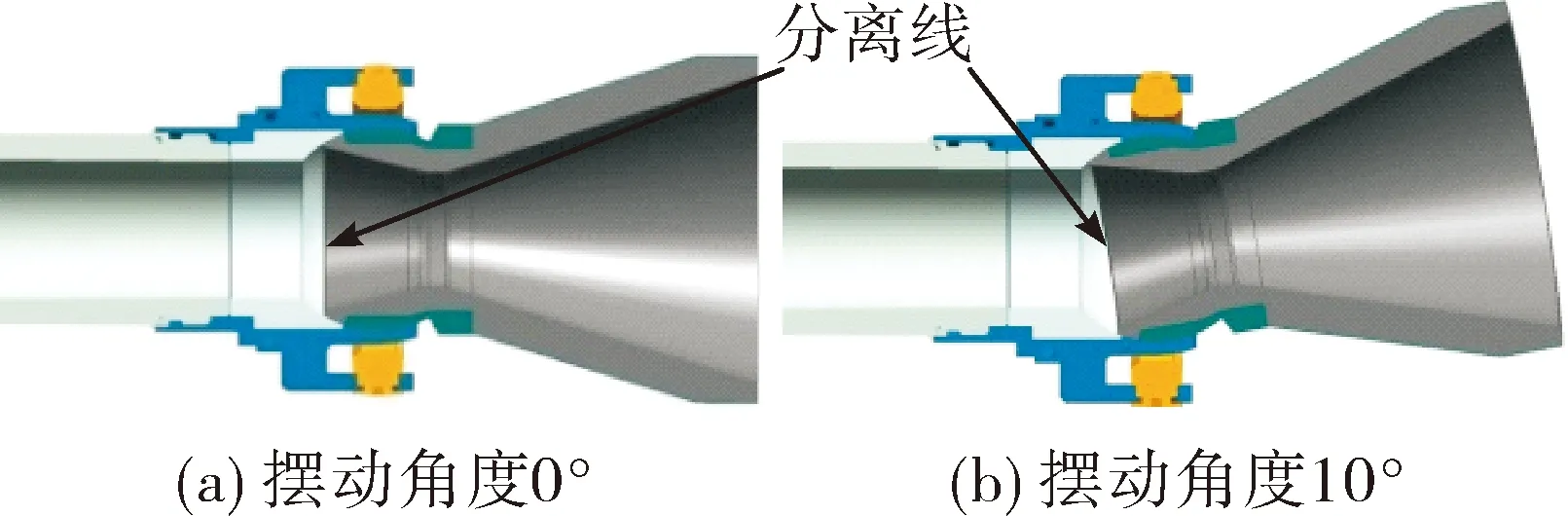
图1 物理模型

1.2 计算网格

根据模型特点采用1/2对称模型，对流体域进行三维网格划分，如图2所示，网格规模约170万，其中分离线处进行了局部加密。

图2 网格划分

2 数值模拟

2.1 计算简化假设

仿真计算采取如下简化假设：

1)不考虑凝相粒子，喷管内为纯气相流动；

2)喷管内的流动为冻结流；

3)不考虑辐射换热的影响。

2.2 计算工况设置

为减轻烧蚀，摆动喷管分离线处预留摆动余量，即分离线处存在一圈凹坑区域，其范围随喷管摆角变化而变化。为对凹坑的影响进行评估，定义内型面参数通喉比J：

J=A/At

(1)

式中:A为分离线处的通道面积；At为喉部面积。

以常规喷管、不同摆角和通喉比的摆动喷管模型为基础设置一系列计算工况。计算模型和工况分别见图3和表1。其中工况0为常规喷管，其几何参数与工况a1相同。工况e1、e2是模拟冷流试验的一种工况，以此作为不同工作介质的对比。

2.3 控制方程

流场计算采用的控制方程为定常三维可压缩粘性流动N-S方程：

(2)

式中：E、F和G为对流通量矢量；Ev、Fv和Gv为粘性通量矢量。

图3 计算模型纵剖面

表1 计算工况

2.4 边界条件和数值计算方法

计算所需的边界条件类型有压力入口、压力出口、无滑移固壁边界和对称面边界等。其中压力入口采用表1所列工况的条件，压力出口采用外界大气压作为出口反压。

计算所采用的数值计算方法详见表2。

表2 数值计算方法

3 计算结果与分析

3.1 喷管流场特性分析

3.1.1 整体流场变化

对比各工况的计算结果，流场具有较大相似性。图4(a)为摆动喷管与常规喷管的马赫数分布对比，常规喷管中的气流加速均匀，而摆动喷管由于分离线处通道的扩张，气流加速减缓，靠近壁面处存在低速区。从喉部到出口的区域内，两者马赫数分布差异很小，最大值为2.97Ma。图4(b)为工况a4即喷管摆至最大角度10°的马赫数分布，分离线处的马赫数随内型面的变化而呈现出不对称分布，但其对下游的整体影响很小，喉部及扩张段内的气流均匀的膨胀加速，至出口仍达约2.97Ma。

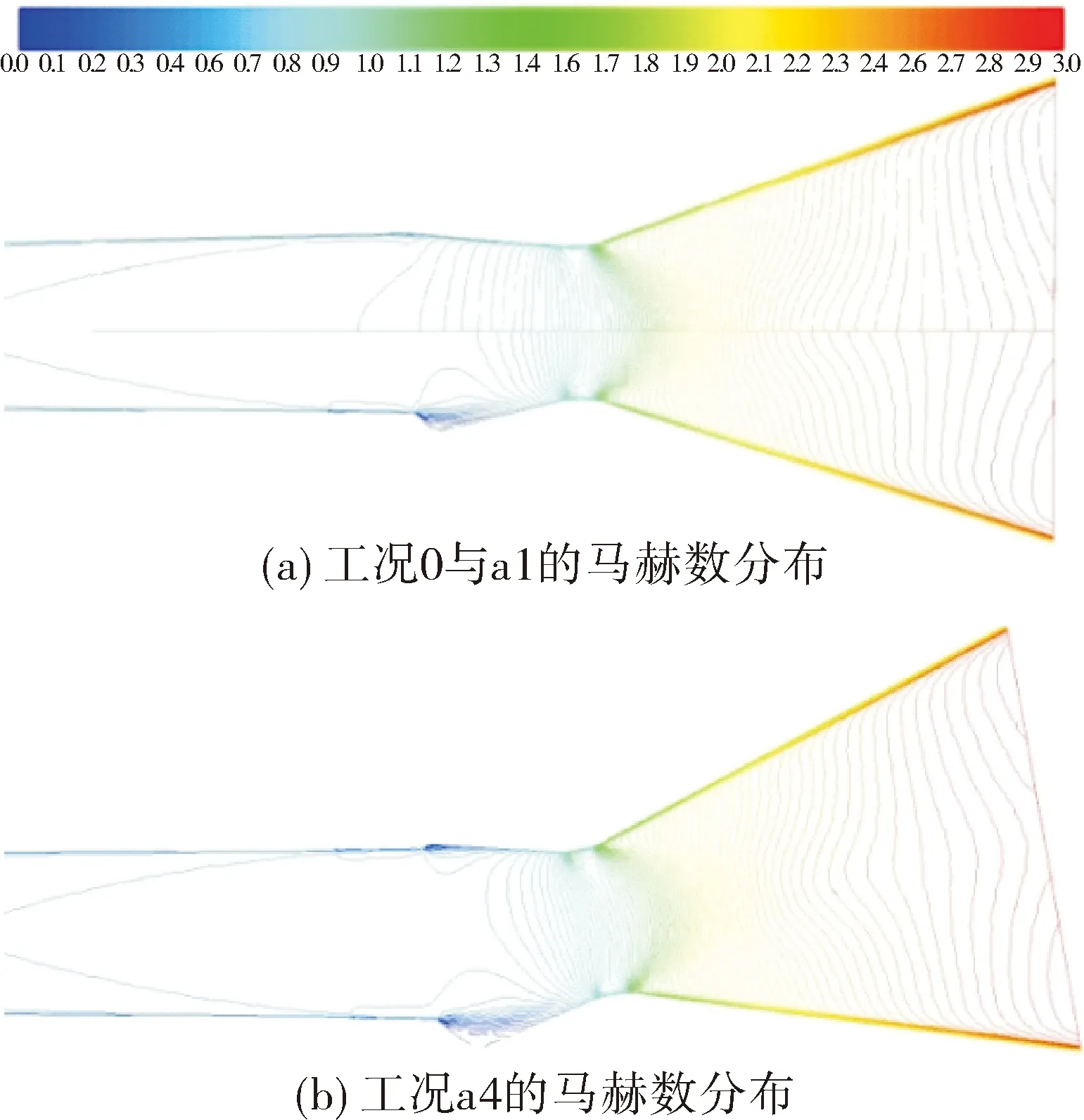
图4 工况0、a1和a4的马赫数分布对比

从整体看，摆动喷管摆动前后的内型面不连续并未对气流的膨胀加速过程造成明显干扰，但与常规喷管相比，摆动喷管在摆动前后始终存在局部的不均匀和不对称现象。

3.1.2 流场局部细节分析

首先对同一个喷管在不同摆角时的流场进行分析。图5和图6分别为a1～a4四种工况的对称面局部压强分布和凹坑内的涡流分布，随着摆角的变化，分离线附近始终存在局部高压和涡流现象，凹坑加深的一侧高压区域逐渐增加，涡流范围也随之扩大，而另一侧则缩小但未完全消失，分离线附近的压强和涡流分布变得很不均匀。

图5 不同摆角的局部压强分布

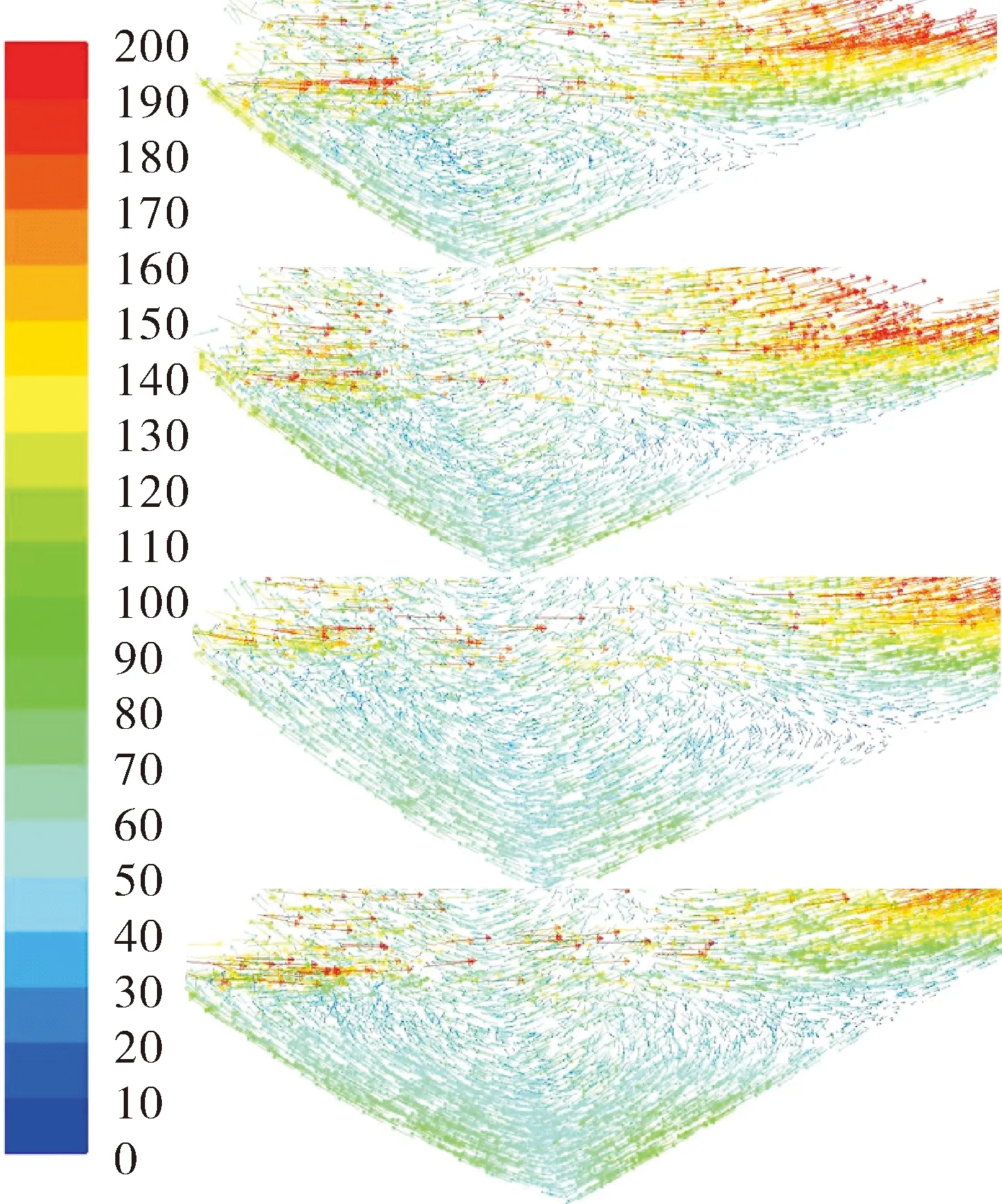
图6 工况a1～a4分离线附近的涡流图

然后观察其它工况的流场，喷管摆动前后的变化趋势与a1～a4的变化基本一致。图7仅显示了几种喷管摆动后的局部压强分布。可以看出，随通喉比的增加，分离线附近的局部压强越来越接近上游入口的压强，压差也越来越小。其它工况的涡流分布形态与a1～a4类似，不再一一展示。

图7 不同工况喷管摆动后的局部压强分布

所有工况的摆动喷管在分离线附近的凹坑内均存在着局部高压和涡流现象。表3为统计的不同工况的分离线压差和最大涡流速度。对比a1～a4的结果可以看出:分离线压差和最大涡流速度基本不受摆角影响，分析原因为摆角变化并未导致通道面积的明显改变，分离线处的整体压强和速度范围基本不变；对比其它工况可以看出:同种状态的喷管，摆动前后的差别都很小，即喷管摆动对流场影响很小。对比工况b1、b2与a1、a4的结果，随压强的降低，分离线压差也相应减小，但最大涡流速度几乎不变。对比b1～d2的工况，随通喉比的增大，分离线压差和最大涡流速度都大幅下降，应是通道面积相对喉部面积的大幅增加而使整体气流速度降低导致的。对比d1～e2的结果，工作介质改为空气后，最大涡流速度明显降低，分析原因为空气温度低致使气流达到的动能低。

表3 不同工况的分离线压差和涡流速度

3.2 喷管性能变化

通过对壁面边界进行积分，得出各工况的轴向力、侧向力等参数指标，结果见表4。其中轴向推力损失的计算，工况a1以工况0为基准，其他工况则以未摆动时的状态为基准。

表4 计算结果数据

由表中数据可以看出:摆动喷管的常值损失仅约0.4%，各工况喷管偏转后的损失都在2%以内。喷管摆动形成的推力偏角基本等于摆角。据推力偏角计算，摆动喷管在10°偏角下可提供17%左右的控制力。根据文献[3]、[11]和[12]，燃气舵在10°舵偏角时提供的控制力约4%，而推力损失达5%，在25°舵偏角时的控制力不到10%，而推力损失超过10%。另外，燃气舵的常值损失通常在3%以上。与燃气舵相比，摆动喷管明显推力损失更小、致偏效率更高。

对比工况a1～a4的推力偏角和轴向推力损失，如图8所示，推力偏角和轴向推力损失随摆角呈线性变化，推力偏角基本等于摆角。

图8 推力偏角和轴向推力损失随摆角的变化

表4最后两列分别表征了喷管摆动造成气流偏转的内流场负载和摆动动作的摩擦力大小，此两者是喷管摆动力矩的主要组成部分。

表中数据显示气动力矩随摆角的增大呈正比例增加，随通喉比的增加呈指数关系减小(图9)。最大气动力矩为5.23 N·m，表明喷管摆动的内流场负载水平不高。

图9 气动力矩随摆角和通喉比的变化

喷管摆动段轴向受力与摆角和工作介质基本无关，与燃烧室压强和通喉比大致呈正比，主要原因是

燃烧室压强决定了壁面附近的气体压力而通喉比则代表了壁面受力面积。假定以轴向受力作为接触面压力，对喷管摩擦力矩进行估算，工况a4的摩擦力矩约44 N·m(摩擦系数取0.1，回转半径0.04 m)。摩擦力矩远大于气动力矩，因此在摆动喷管设计时，当燃烧室压强确定后，在一定范围内减小通喉比，既能使气动力矩处于较低水平，又能显著降低摩擦力矩，从而减小摆动力矩。