履带式车载武器行进间发射动力学研究*
2019-12-28麻小明刘馨心徐宏斌薛海瑞
麻小明,刘馨心,徐宏斌,薛海瑞,李 庚
(西安现代控制技术研究所, 西安 710065)
0 引言
车载武器在行进过程中,除了受到火力系统的反作用力之外,还受到来自地面的随机振动激励,在这种随机振动作用下战车姿态容易产生较大变化,文中以履带式车载导弹武器系统为研究对象,根据路面不平度位移功率谱构造符合国家标准的各级路面,利用多体动力学软件在各等级路面和不同车速下进行行进间发射仿真计算,研究该武器系统在不同路面及不同行进速度等环境因素条件下的载荷传递路径及动态响应特性,获得武器系统发射稳定性和发射安全性边界条件,为车载武器行进间发射提供理论依据,对于安全发射提供指导。
1 路面随机振动激励研究与模拟
车辆行进时受到路面或轨道表面不平度的激励所产生的随机振动,是车辆振动的主要原因,它对于车辆乘坐的舒适性、安全性、耐久性等都有重大影响,工程界普遍认为基于随机振动理论的功率谱方法是最为合理的方法[1]。
1.1 路面不平度理论
国际标准化组织(ISO)和我国GB/T7031—2005均建议采用式(1)功率谱密度函数拟合[2]:
(1)
其中:n为空间频率,它是波长λ的倒数,表示每米长度中包括几个波长,单位m-1;n0为参考空间频率,n0=0.1 m-1;Gq(n0)为参考空间频率n0下的路面谱值,称为路面不平度系数,单位m3;W为频率指数,为双对数坐标上斜线的斜率,它决定路面谱的频率结构。
目前,路面谱模型的建立方法主要有4种[3]:滤波白噪声法、泊松过程模型、AR模型参数法和谐波叠加法。贾进峰等[4]分别对以上前3种方法进行分析、建立模型以及验证,从验证结果中可以得出采用谐波叠加法建立的路面不平度更准确,但是只进行了二维路面模型的建立,并未考虑由于路面左右不对称带来的影响。谢润[3]对以上4种方法进行介绍,并根据谐波叠加法建立了二维路面,利用两侧车轮所受路面激励的相干函数建立三维路面不平度模型,该方法计算较复杂。钟洲等[5]采用AR模型参数法对不同等级随机路面进行数值模拟,建立了轮式车载防空导弹行进和发射一体化动力学模型,确定了导弹行进间发射的允许路面和车速。陈余军等[6]采用三角级数法模拟路面,并对车载导弹进行动力学仿真,但未能考虑路面随机因素的影响。文中采用谐波叠加法,将二维计算模型扩展到三维,生成路面不平度模型。
1.2 谐波叠加法
谐波叠加法基本原理是认为路面不平度可由大量正弦波组成,其数学推理严格,涉及到许多三角函数,运算量较大。
式(1)是基于空间频率的表达式,由车速和时间频率之间的关系可以写出时域下的表达式[7]:
f=vn
(2)
(3)
式中:f为时间频率,单位Hz;v为车速,单位m/s。
路面不平度的方差可以表示为:
(4)
将f(fmin (5) 将N个正弦波叠加就可得到随机路面垂直位移的时域表达式: (6) 式中:q(t)为时域下路面高程;θi为[0,2π]的随机数。 将式(6)写成空间域内的表达式: (7) 根据谐波叠加法,采用Matlab数学工具编写计算程序,生成符合我国道路分级标准的1 000 m长的D级路面,如图1所示。对模拟生成的路面进行验证,由图2可以看出模拟路面能够较好的反应真实路面状况。 图1 D级二维路面 图2 功率谱密度 将式(7)扩展为x方向和y方向,得到三维空间下的路面不平度关系式: (8) 式中:θi(x,y)为均匀分布在[0,2π]上的相互独立的随机变量;x,y为路面纵横向行程,单位m;q(x,y)为三维空间内的路面高程,单位m。 利用Matlab生成宽5 m长80 m的三维路面,如图3所示。 图3 D级三维路面 车载导弹行进间发射时的环境因素非常复杂,除系统内部各部件之间的相互作用力之外还受到来自于地面的冲击,为了更全面的模拟行进间发射的环境因素,采用虚拟样机技术对战车行进间发射状态进行预测分析与研究。 为简化计算和节省时间,作如下合理假设: 1)忽略发动机运转时产生的振动,直接在驱动轮上施加载荷; 2)战车沿着路面直线行驶,不考虑横向滑动; 3)假设弹簧为线性弹簧,且各负重轮与底盘之间的连接刚度和阻尼相等。 模型主要分为两大部分,底盘和发射装置(含弹箭),两者之间由弹簧阻尼器连接,底盘由负重轮支撑,平衡肘总成简化为弹簧阻尼器,在第一、二、五负重轮与底盘之间采用弹簧阻尼器,第三、四负重轮上采用线性弹簧。 图4 系统动力学模型 三维空间中的每个刚体包含6个自由度,3个平动,3个转动。对于N个刚体组成的系统,位置坐标阵q中的坐标个数为6N,由于铰约束的存在,这些位置坐标并不独立,应用拉格朗日待定乘子法,可以建立车载武器多体系统动力学方程 (9) 武器系统动力学模型中各构件之间存在许多接触,弹与发射筒内壁、履带传动系统中履带与驱动轮、诱导轮、负重轮和拖带轮之间存在接触。如何准确计算构件之间的接触力,对于发射动力学仿真精度具有重要意义。文中计算接触力是基于Hertz接触理论,并在此基础上做了改进[8]。 计算接触产生的法向接触力公式为: 摩擦力为: ff=μ|fn| 式中:μ为摩擦系数,其符号和数值由接触位置接触对的相对速度决定。 影响行进间发射动力学的两个重要因素是行车速度和路面等级,通过在相同路面不同速度下和相同速度不同路面下进行仿真分析,对武器系统行进间发射状态进行预测分析与研究。 在D路面分别以10 km/h,15 km/h,25 km/h,30 km/h,40 km/h的车速进行仿真,得到战车稳定行驶后的动态响应曲线,限于篇幅,文中只给出垂直方向的位移和俯仰角位移曲线如图5、图6所示。 图5 战车振动位移 图5中所示为战车底盘质心垂直方向的位移,图中给出了5种车速下的位移-时间曲线,可以看出在较高车速(40 km/h)和较低车速(10 km/h,15 km/h)下战车振动幅度较大,中等速度 (20 km/h,30 km/h)下振动幅度较小,因为随着车速的变化,路面激励的频率也在变化,当路面激励的频率与多自由度战车系统的各阶固有频率接近时,战车系统会产生共振现象[9]。因此,车速对于战车垂直位移的影响呈波动规律,在战车行进间发射时并非车速越低越好。 图6 战车俯仰角位移 图6所示为战车绕横轴转动角位移曲线,其变化规律与战车位移曲线基本相同,表1给出了不同车速下角位移均方根值,从表中也可以看出低速和高速情况下均方根值较大。 表1 战车角位移均方根 以40 km/h的车速分别在C、D、E 3种路面进行仿真,得到战车垂向振动位移和俯仰角位移如图7、图8所示。 图7 战车振动位移 由图7和图8可以看出,随着路面等级的增加,战车振动幅度和俯仰角的变化增大,因此路面状况对于车载武器行进间发射具有较大影响。 图8 战车俯仰角位移 战车行进间发射时受到地面的随机激励,因此导弹出筒时姿态角也具有随机性。文中通过改变发射时刻,进行多次仿真的方法对姿态角变化进行统计分析,图9所示为行进间发射时变化较大的俯仰角速度的仿真结果范围统计。表2给出了多次仿真俯仰角和俯仰角速度的最大值。 图9 导弹俯仰角速度 表2 导弹俯仰角速度与俯仰角 从图9中可以看出,俯仰角速度随着行驶速度和路面等级增加而增大,具体数值见表2。 由表2中所给数据可以看出行进间发射时导弹出筒时刻俯仰角速度较静止发射时增大,在C级路面下以15 km/h发射时最小,E级路面以40 km/h发射时最大;在同一等级路面下车速对俯仰角的影响随机性较大,与战车质心垂向位移的变化趋势相同,呈波动规律;不同路面下俯仰角速度随着路面等级增大而增大。 文中根据国标给出的路面不平度表示方法,利用谐波叠加法模拟出各等级路面,采用虚拟样机技术建立某车载武器动力学模型,将试验获得的弹推力及后坐力曲线数据加载到模型中,分别在不同等级路面,以不同车速进行仿真分析。研究表明,采用谐波叠加法模拟的路面功率谱密度与理论功率谱密度吻合,可以作为仿真输入;总体而言,速度越快,路面状况越差,战车行进间发射的外部坏境越恶劣,导弹初始扰动越大;给出了某车载武器装备在常见3种等级路面和3种速度下导弹出筒时的姿态角变化,C级路面下,行进间发射时俯仰角速度分别增加了46.4%、60.7%、67.9%,D级路面下增加了57.1%、75%、82.1%,E级路面下增加了100%、110.7%、117.9%,为行进间发射稳定性和发射安全性提供参考。
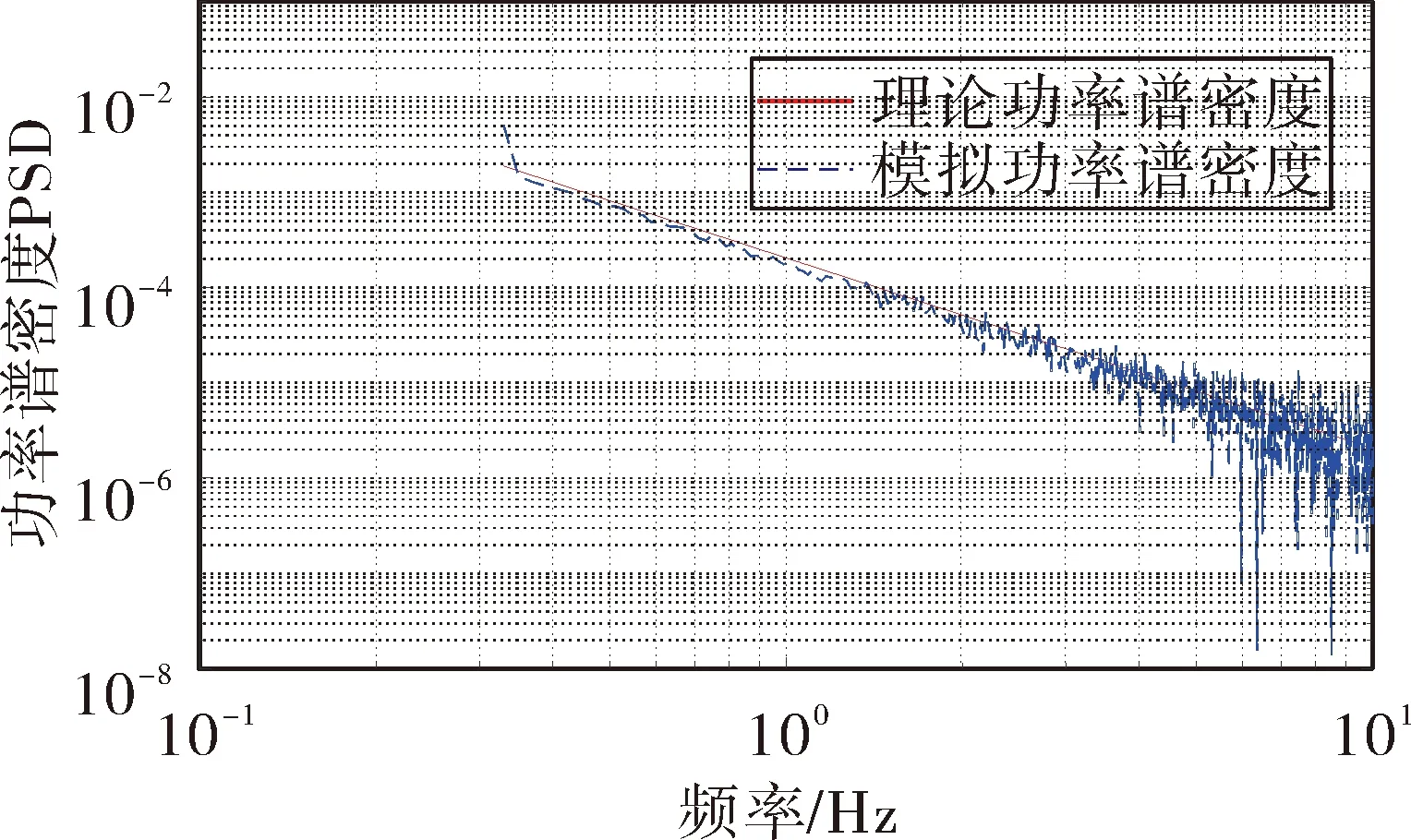
1.3 虚拟路面模型建立
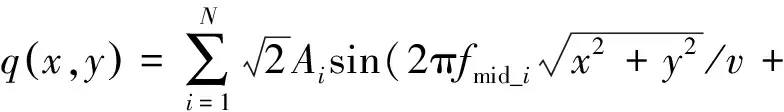

2 系统动力学模型研究
2.1 模型假设
2.2 系统动力学模型
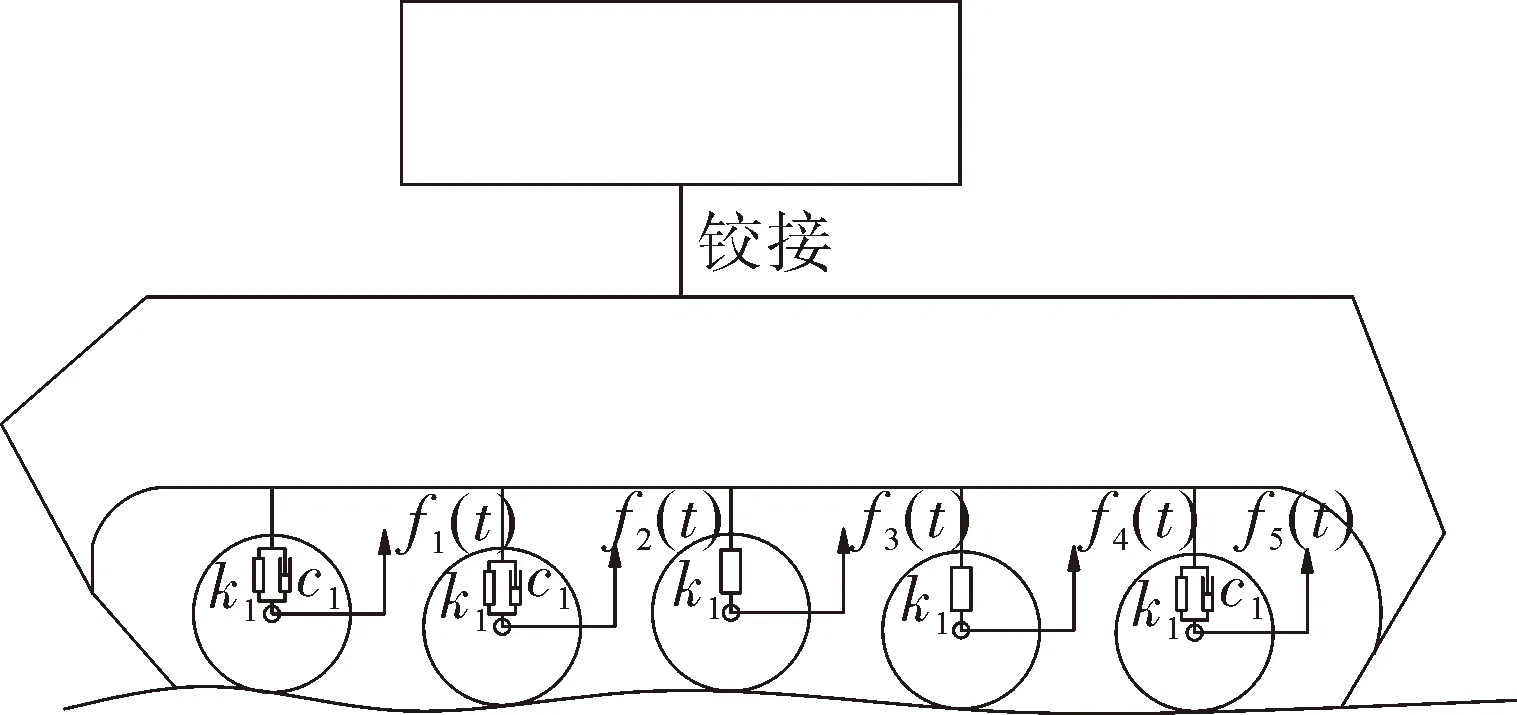
2.3 车载武器动力学方程
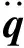
2.4 基于赫兹理论的接触算法
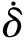
3 行进间发射动力学仿真研究
3.1 车速对行进间发射动力学影响
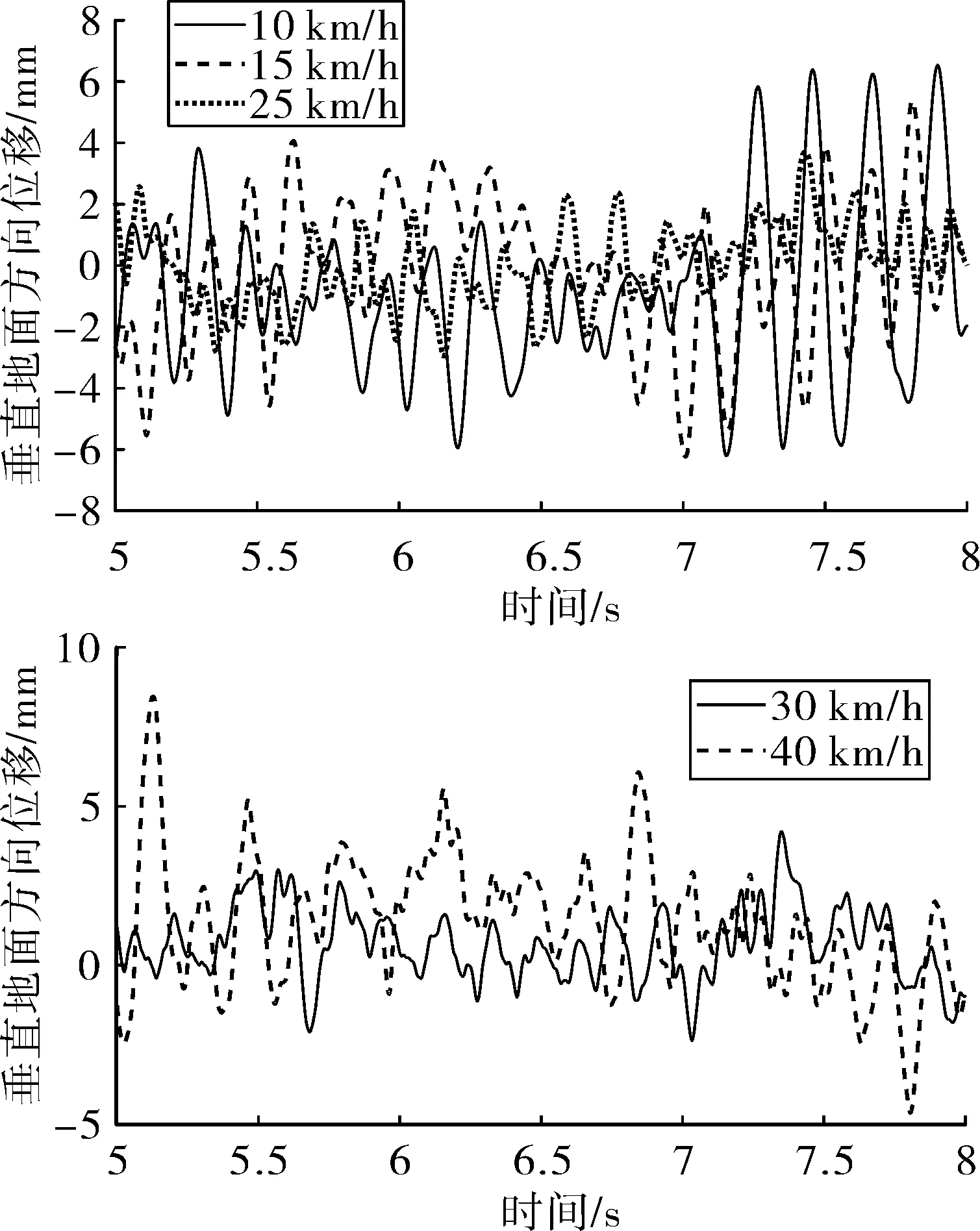
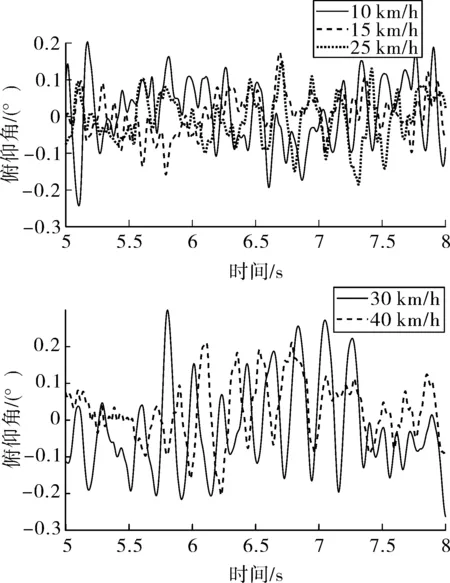
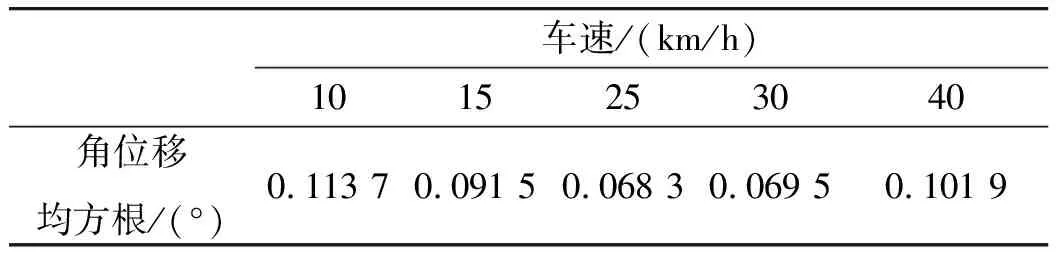
3.2 路面对行进间发射动力学影响

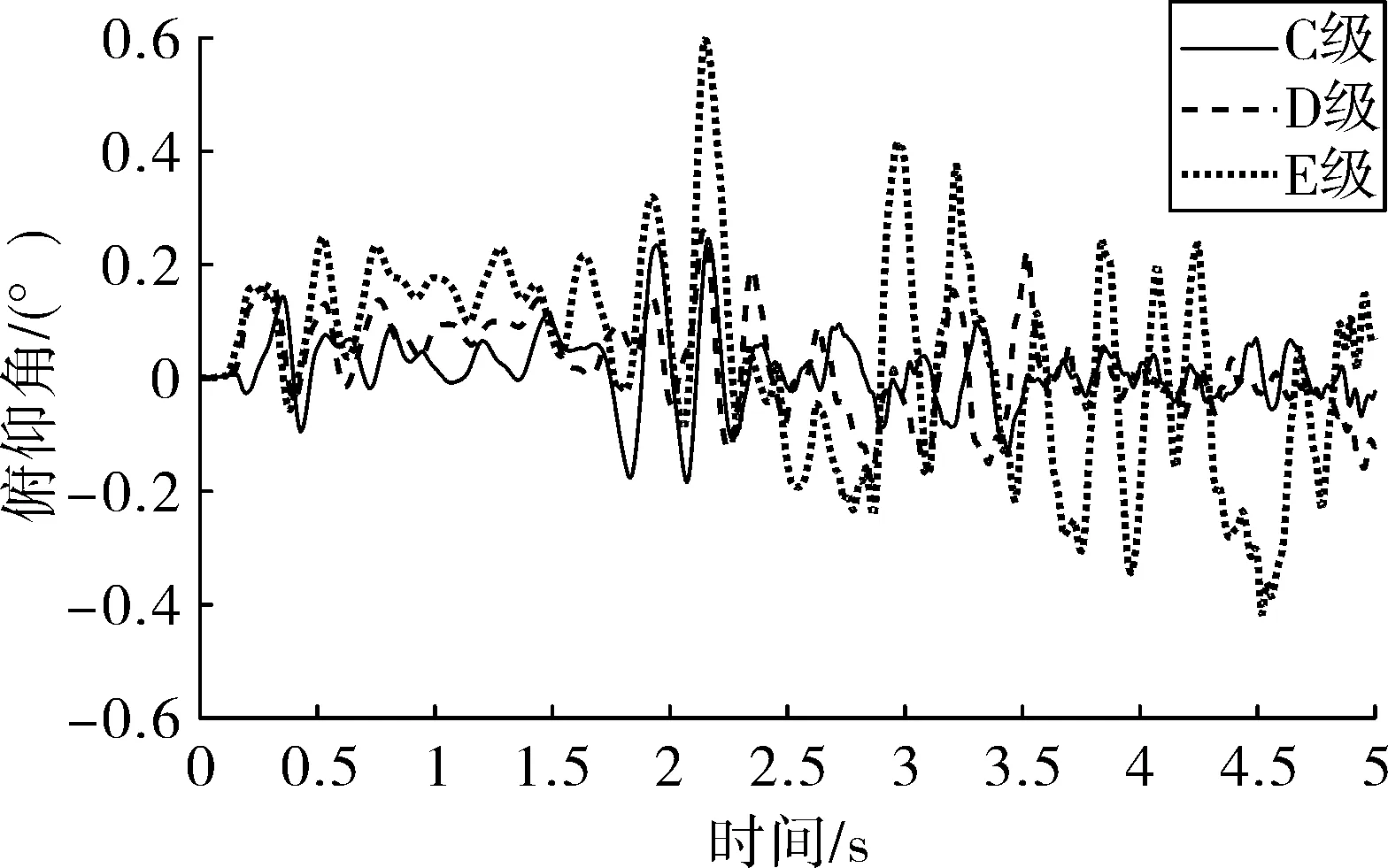
3.3 导弹初始扰动分析
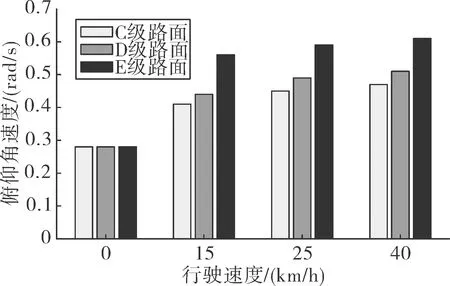
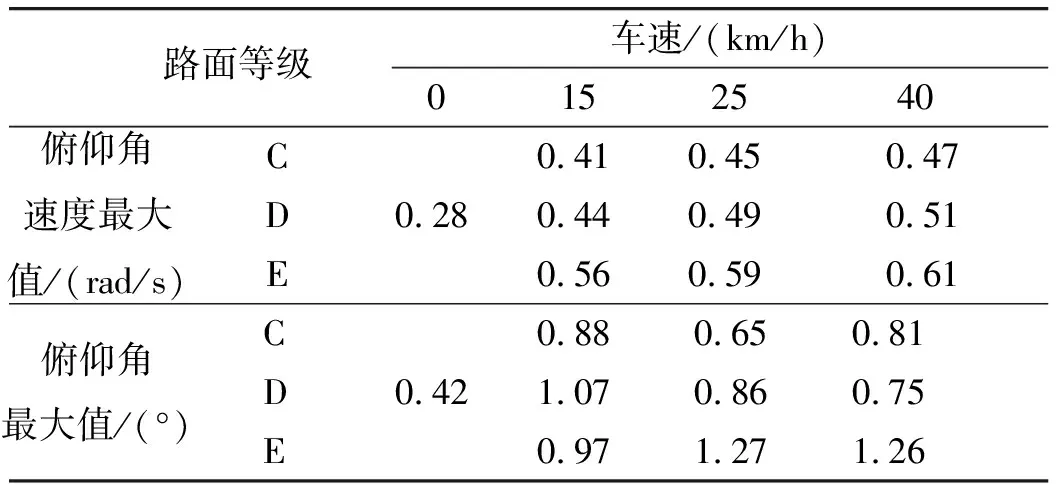
4 结论
