一种确定反舰导弹末制导开机点的算法*

董 斐,欧阳中辉,刘文彪,李 钊

(海军航空大学, 山东烟台 264001)

0 引言

随着反舰导弹射程的增加,导弹飞行过程中产生的惯导导航误差增加,导弹理论开机点与实际开机点之间的偏离误差增大。因此需要通过确定一个合格的理论开机点,来避免开机点误差散布带来的影响,并减小装订截获跟踪状态字的难度。

但是目前还没有一个较为成熟的辅助决策系统可以直接完成这项工作。文献[1]的模型计算了反舰导弹在多目标环境下对预定目标捕获概率,并以此选择开机点,文献[2]在文献[1]概率计算法的基础上考虑了雷达捕获模式对捕捉概率的影响。但这两个模型仍存在以下问题：

1)这些模型在进行态势推演时未采用大地坐标系。这样既降低了模型的实用性,又忽略了大地曲率对整个模型的影响。

2)传统模型选择开机点时采用方法为穷尽点法与蒙特卡洛法,为了提高结果可靠性,计算每一个开机点处的捕获概率时都需要处理成百上千个样本,计算量过大。

与传统模型不同,文中选择开机点的思路是：首先根据捕获概率要求,直接划定符合要求的开机点选择范围,然后根据各项战术要求对范围内开机点进行筛选,直至选择出最符合战术要求的开机点。

其次需要在大地坐标系的基础上完成战场模型的构建,并将距离、角度等二维平面信息实时解算为经纬度方位角等信息并进行推演。

1 坐标系构建

文中模拟的战场环境为我国东南沿海附近,因此采用新1954北京坐标系(简称8054系)。该坐标系采用了克拉索夫斯基椭球体参数,椭球面与似大地水准面和我国境内的实际大地环境最为接近。椭球体参数为：长半轴a=6 378 245 m,短半轴b= 6 356 863 m,扁率α= 1/298.26。

采用Bowring公式完成大地解算工作。有研究表明：Bowring在1 500 km以内结算误差只有10 m[3],解算用的公式系如下：

(1)

2 构建开机点误差处理模型

当导弹到达开机点时,导弹所在的可能位置是一个以理论开机点为中心,最大飞行轨道偏移为半径所围成的一个误差散布圆,导弹分布的概率符合二维正态分布,分布参数为:μ1=μ2=0;ρ=0；σ1=σ2,σ1与σ2的取值由导弹参数、发射点参数、航路点参数与战场环境参数决定[4]。文中通过采用边界点法处理该模型里的误差散布。

边界点法思路如下。R为规定的捕获概率要求下的最大的误差散布圆半径。如果在该误差散布圆内,无论导弹在哪一个点上都能捕捉到预定目标,则在该误差散布圆的圆心开机时能捕获到预定目标的概率一定高于战术要求。若从误差散布圆内提取出最难以满足战术要求的点,而这些点都能满足要求,则误差散布圆内任意一点都可以捕捉到预定目标。由于这些点大都位于模型中各个区域的边界上,因此笔者称该方法为边界点法。

图1为误差散布圆内导弹雷达搜索范围示意图。点T为目标,点O为误差散布圆的圆心。点A与点B为点T与点O连线延长线与误差散布圆的两个交点。点C与点D为过O点做误差散布圆的两条切线时切线与误差散布圆的两个交点。设：Am为导弹攻击方向,AOT为从点O到点T的方位角,SOT为点O到点T之间的距离,Smax与Smin分别为雷达搜索范围的远界与近界,Rmax为雷达搜索范围中的角度范围。

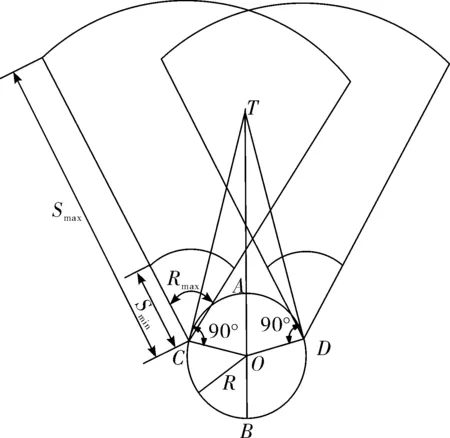
图1 误差散布圆内导弹雷达搜索范围

显然当目标在雷达搜捕范围内目标才能被捕捉到,即

(Smax≥SOT≥Smin)∩(|AOT-Am|≤Rmax)(2)

则说明导弹处于散布圆中心点开机时可以捕捉到目标。显然点A与点B分别为误差散布圆内距离目标的最近点与最远点,点C与点D到点T的方位角与导弹攻击方向的夹角最大。因此若点A、点B、点C、点D及4个边界点皆可以捕捉到目标,散布圆内任意一点都可以捕捉到目标。因此当且仅当满足以下条件时导弹在该开机点处开机时定能捕捉到预定目标。

(SAT≥Smin)∩(SBT≤Smax)∩
(ACT≤Rmax)∩(ADT≤Rmax)

(3)

3 搜捕雷达分辨率影响分析

导弹搜捕雷达具有一定的分辨率。若两个目标与导弹的方位角过于接近,导弹则难以分辨从而可能攻击错误目标或从两目标间穿过。若两目标与导弹间的距离过于接近,两目标回波的时间过于接近,则雷达可能遗漏目标[5]。

设点T为预定目标,点A为导弹,Am为导弹攻击方向,除预定目标外有I个目标,Ami为导弹到某个非预定目标的方位角,Smi为导弹到某个非预定目标的距离,Amin为雷达角度分辨率,Smin为雷达距离分辨率。当满足式(4)条件时雷达在捕捉预定目标时不会因为分辨率问题受到其他目标的影响。

(4)

4 模型仿真

远程侦测平台测得目标编队,编队由3个目标组成,以航速20 kn,航向96°运行,目标2为需要打击的预定目标。目标坐标如表1所示。

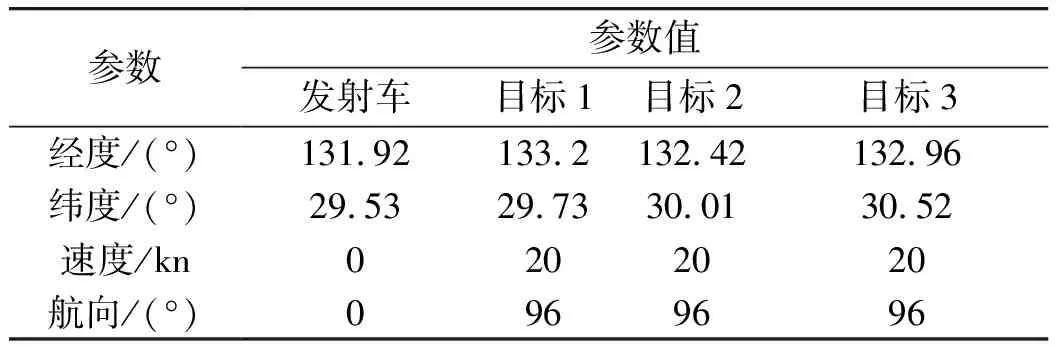
表1 敌我方目标诸元参数

其他重要战场参数为:

1)导弹攻击角要求为60°;

2)我方导弹末制导雷达搜索范围为10 000～50 000 m,角度范围为90°;

3)我方导弹末制导雷达距离分辨率为2 km,角度分辨率为2°。

根据我方某型导弹相关资料所提供的相关参数与雷达捕捉预定目标的概率要求,计算得到误差散布圆半径为11 km。仿真软件结构如图2所示。

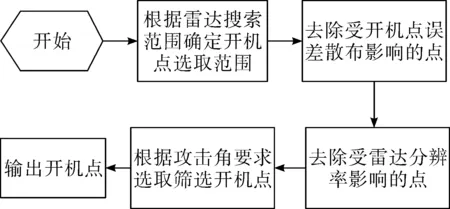
图2 软件工作流程示意图

最佳开机点应该做到导弹到达开机点时雷达开机便可以搜索到预定目标。因此最佳开机点分布范围为围绕预定目标一周,分别以雷达搜索的近距与远距为内半径与外半径的一个环形区域。采样点的位置信息以极坐标表示。0°指向正北方向,距离单位为 km。将以上数据输入仿真软件中得到以下结果。

战场态势图如图3所示。

首先根据上述模型确定开机点选取范围。结果如图4所示。

获取可能开机点后,需要用边界点法进行筛选。筛选结果如图5所示。显然,越靠近搜索范围边界的地方越容易受到误差散布圆的影响。

如第3节所述,若两个目标与导弹的方位角过于接近或两目标与导弹间的距离过于接近,捕捉任务都会受到雷达分辨率的影响,降低了捕获预定目标的成功率,因此存在以上两种情况的开机点应予以去除,去除结果如图6与图7所示。

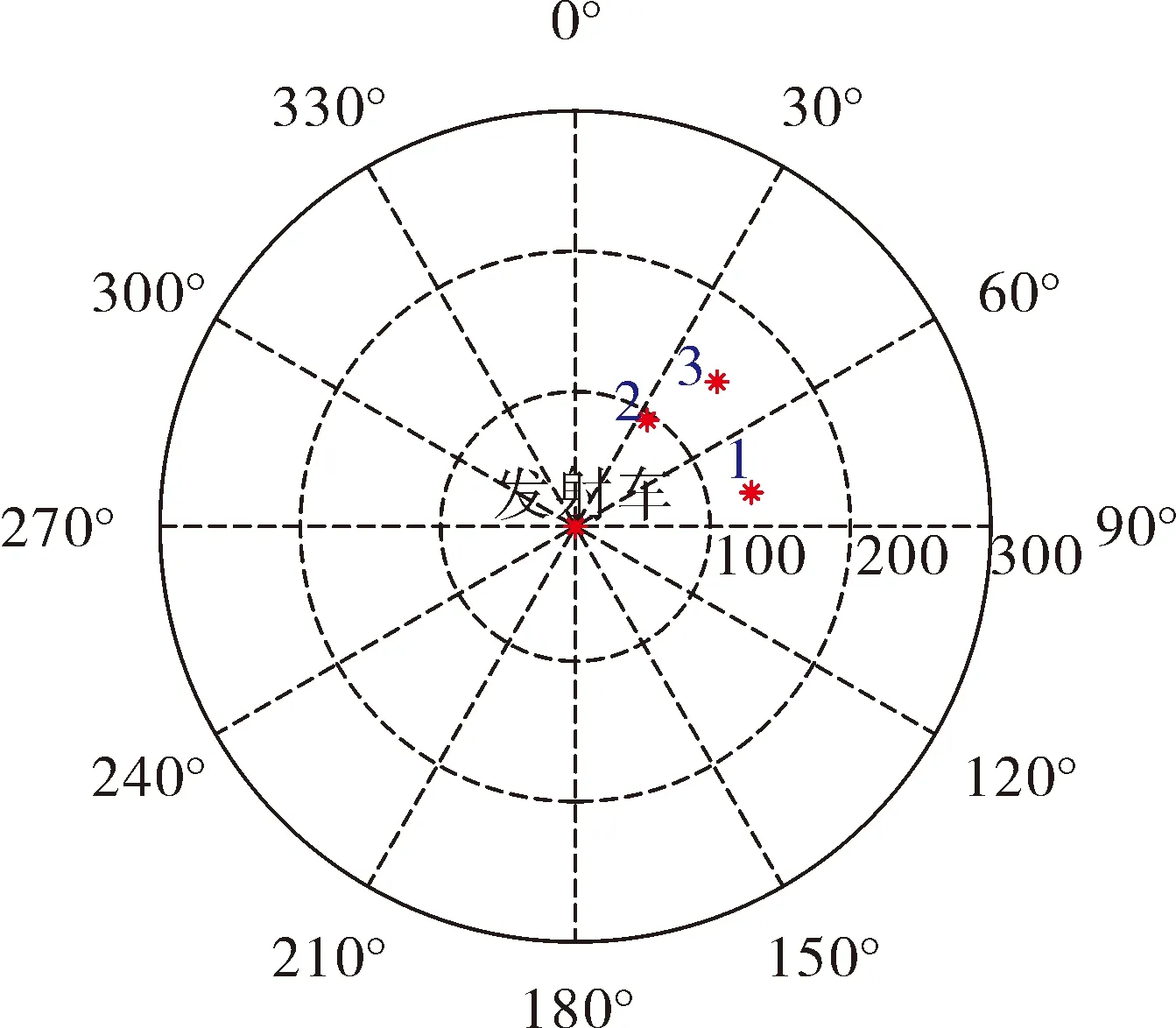
图3 战场态势示意图

图4 穷举范围示意图

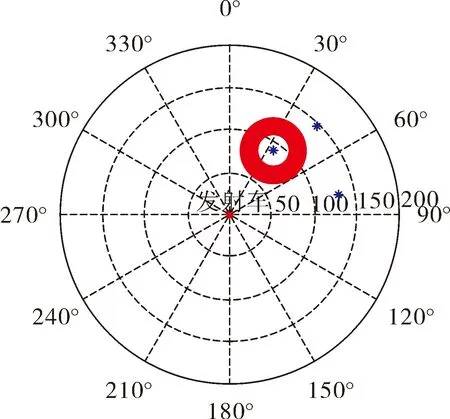
图5 边界点法处理结果

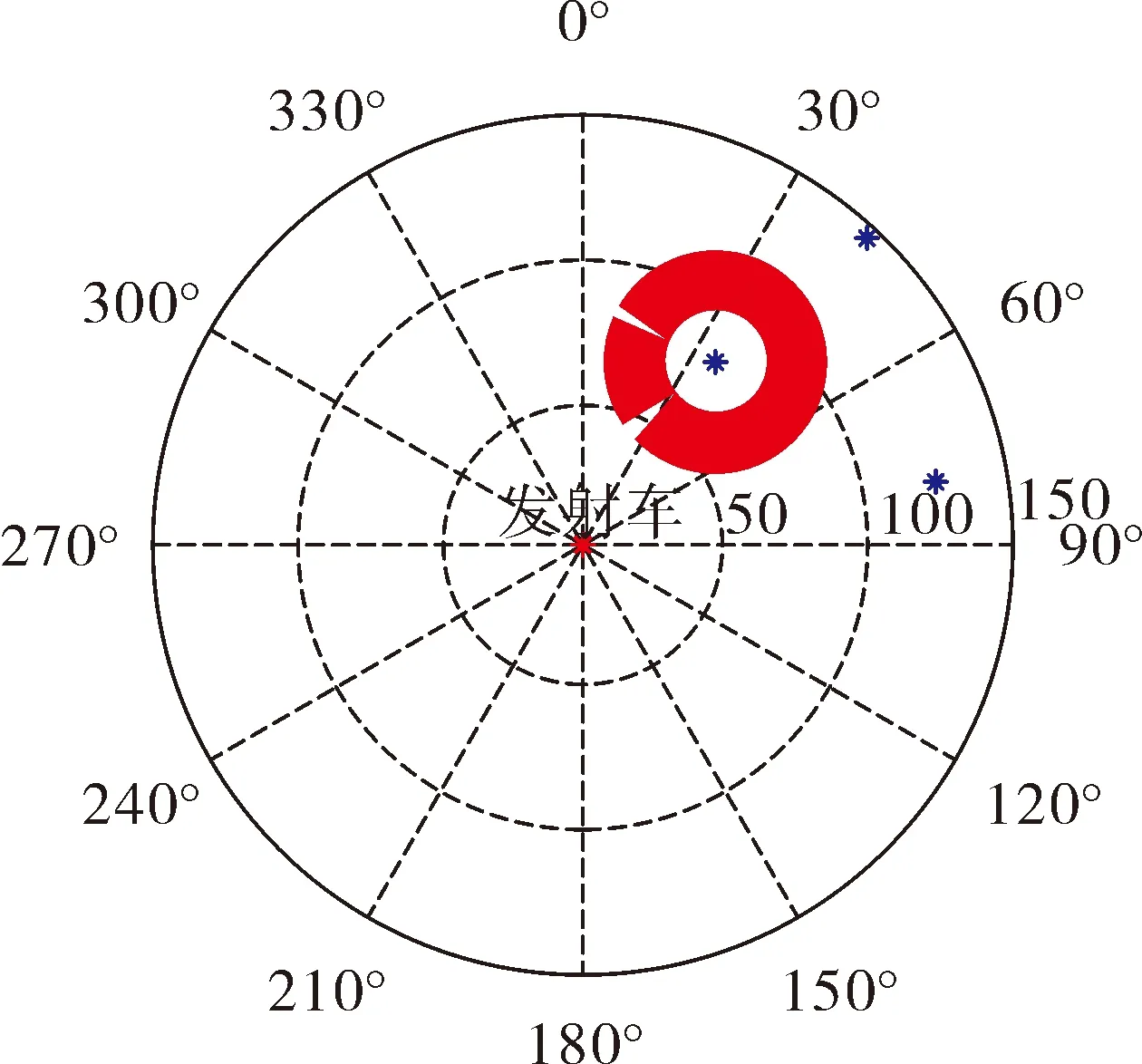
图6 去除受雷达角度分辨率影响的点

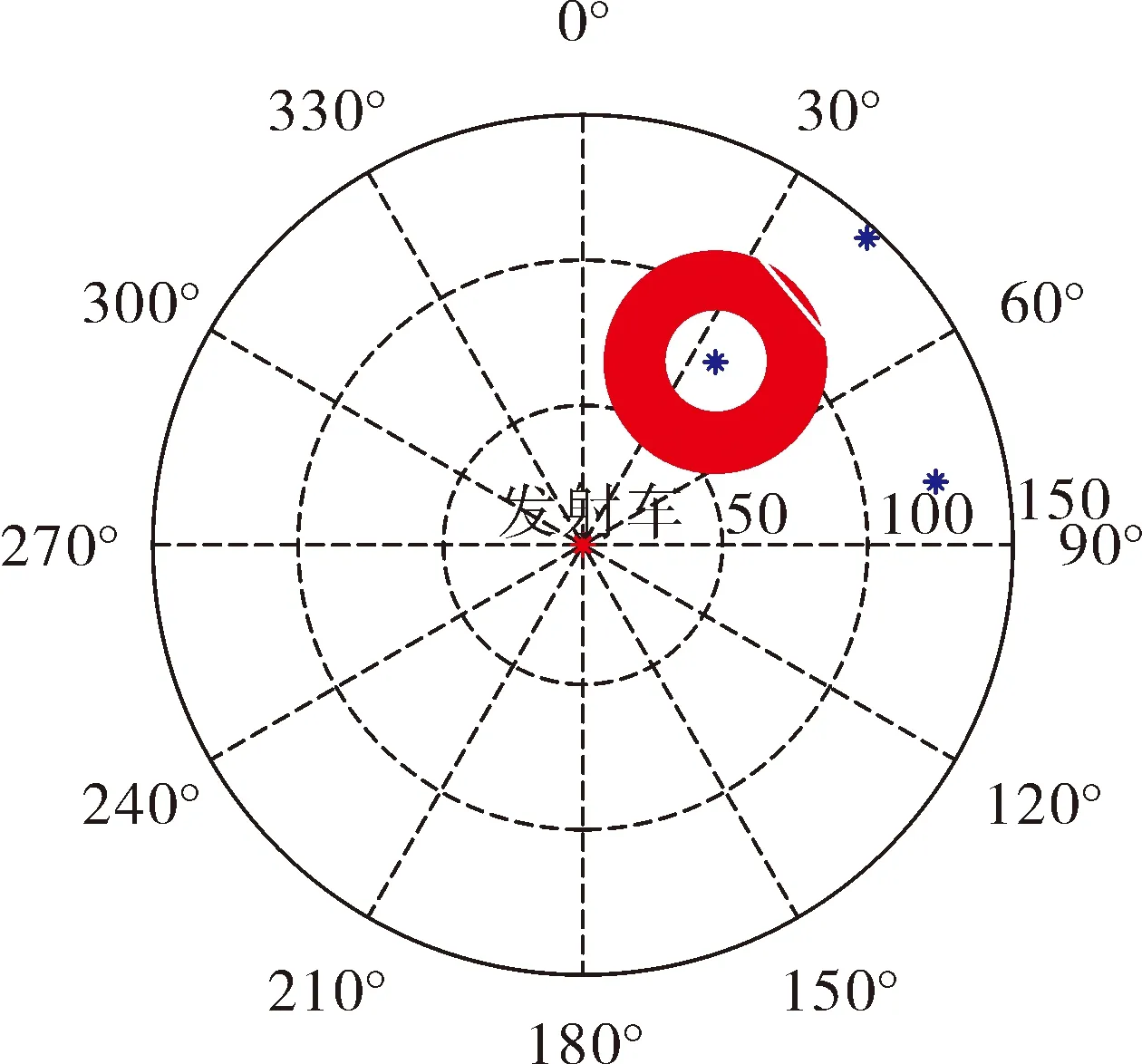
图7 去除受雷达距离分辨率影响的点

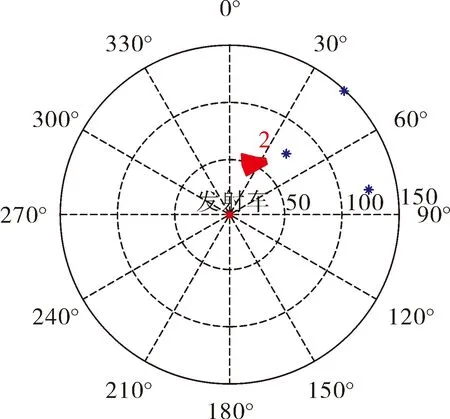
图8 最符合目前战术要求的点

经过以上两步筛选,得到的开机点都是捕捉概率达到战术要求的开机点。最后需要通过再次使用边界法选取攻击角符合要求的攻击点。同理,越靠近雷达搜捕范围边界点的位置越容易受到开机点误差散布的影响,越容易被边界点法淘汰。因此选出的开机点角度范围小于雷达的搜索范围。选取结果如图8所示。

通过仿真结果可知,该开机点选取模型能够快捷有效地根据战场态势选取出满足战术要求的开机点。

5 结论

开机点选取工作是整个战场信息辅助决策系统的一部分,因此除战场态势因素还有众多因素需要研究者考虑,如位置较为偏僻的开机点会怎样影响航路规划,同捕捉概率的开机点会如何影响战术毁伤效果,而这就是完善该模型需要考虑的方向。