带隔板装药爆轰波驱动药型罩数值模拟研究*
2019-12-28张建军侯云辉刘燕宁
潘 建,张建军,侯云辉,刘燕宁
(西安现代控制技术研究所, 西安 710065)
0 引言
在常规武器系统的设计中,聚能装药战斗部扮演着越来越重要的角色,提高炸药能量利用率是战斗部设计者追求的目标之一。通常而言,采用环形或多点起爆、高低爆速的夹层装药和带隔板装药等结构可有效提高炸药能量利用率。其中,带隔板装药不仅结构简单而且可以在减少装药量以及不改变装药长径比的条件下,提高其对药型罩的压垮做功能力。
国内外学者针对带隔板装药驱动药型罩的作用过程开展了深入的研究。张先锋等人[1]对带隔板装药EFP成型进行了相关研究,数值模拟和实验结果均表明,相对于无隔板装药,带隔板装药所形成EFP具有较高的速度和较大的长径比。张彦国等[2]利用JWL和Lee-Tarver模型对带大隔板装药爆轰波的传播过程和EFP成型分别进行了数值计算,计算得出带大隔板装药结构可以提高EFP的速度。门建兵等[3]分别利用3种敏感探测结构(平板天线、波导管中馈和波导管边馈)对EFP的成型进行了数值模拟研究,结果表明中馈波导管结构通过进一步优化可以得到满意的EFP形状。朱传胜等[4]对带隔板中空装药的EFP成型进行了数值研究,最终优化设计了一种弧锥结合罩结构,试验结果与数值模拟结果吻合较好。
文中的研究在前人工作基础上,利用AUTODYN有限元计算程序中基于炸药冲击起爆的Lee-Tarver模型对三种带隔板装药(SCJ、JPC和EFP)爆轰波驱动药型罩进行数值模拟计算。
1 带隔板装药爆轰波传播过程分析
爆轰波绕过隔板后,在轴线位置处相互作用后发生正规反射或马赫反射(超压爆轰),反射压力将超过CJ压力,以pentolite(50/50 TNT/pentaerythritol tetranitrate)为例[5]。爆轰波在带隔板装药的传播过程中,随入射角的增大,发生正规反射和马赫反射后反射压力与CJ压力的比值如图1所示。计算结果表明:当发生正规反射时,反射波压力与CJ压力的比值基本恒定,达到2.4;当刚发生马赫反射时,马赫杆上的压力与CJ压力比值最大为3.8,最小为2.7;随着入射角再次增大,马赫杆上的压力值迅速降低,最终达到CJ值。根据文献[6]知,带隔板装药结构爆轰波相互作用发生马赫反射后,马赫杆的高度值不断变化。

图1 反射波压力随入射角变化的计算结果
通过计算可以得出:在相同装药结构中,适当增加隔板直径不仅可以有效改变爆轰波传播方向,提高爆轰波对药型罩的压垮能力,而且可以有效增大马赫杆的高度。为下一步带隔板装药驱动药型罩的数值计算提供理论依据。
2 数值模拟
2.1 有限元计算方案
根据对带隔板装药爆轰波驱动药型罩过程的初步分析[7],在保证隔板外侧爆轰波可以正常传播的条件下,隔板直径尺寸越大,调整爆轰波形状的能力越强,在装药结构中爆轰波驱动药型罩的能力越强。
带隔板装药爆轰波驱动药型罩是一种多物质相互作用的大变形运动过程,文中的研究采用多物质耦合的Euler算法分析带隔板装药爆轰波驱动药型罩过程。
2.2 材料模型
爆轰产物的JWL状态方程可以精确描述爆轰波未到达隔板以及在隔板侧面时爆轰波膨胀传播过程。
(1)
式中:P为爆轰产物的压力;V为爆轰产物相对比容;E为爆轰产物的比内能;A、B、R1、R2、w为待拟合参数。
药型罩材料为高导无氧铜(OFHC),采用Johnson-Cook模型,状态方程为Gruneisen方程。隔板材料为环氧树脂(BORON EPXY),状态方程为Puff状态方程。药型罩、隔板材料和炸药参数主要来自文献[8-9]及AUTODYN中内置的参数,其中TNT、B炸药和8701炸药的爆轰参数分别为:TNT炸药的ρ=1.63 g/cm3,D=6.93 km/s,PCJ=21.0 GPa;B炸药的ρ=1.717 g/cm3,D=7.980 km/s,PCJ=29.5 GPa;8701炸药的ρ=1.70 g/cm3,D=8.425 km/s,PCJ=30.0 GPa。
3 数值仿真结果与分析
3.1 隔板结构对高速射流(SCJ)数值仿真计算
SCJ装药结构参数来自于文献[10]中的参数。采用中心起爆和Comp B炸药,其状态方程参数如2.2节所示,装药直径为86.3 mm,长度为152.4 mm。采用单锥形药型罩,其锥角角度为42°,壁厚为2.69 mm,罩口直径为86.3 mm。
为了探讨隔板结构对高速射流的速度和长度的影响,首先开展了有无隔板结构压垮药型罩的数值模拟,高速射流装药结构及射流成形结果如图2所示。与不带隔板装药相比,带隔板装药结构尺寸相同,圆台形隔板最大直径为60.42 mm,厚度为25 mm,采用酚醛树脂材料。
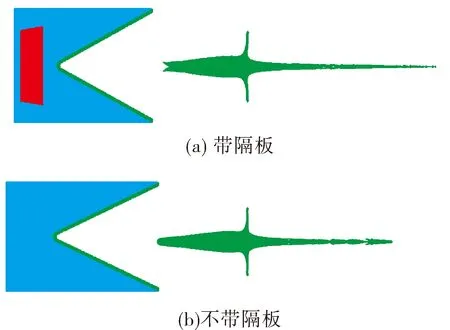
图2 有无隔板装药结构及射流成形结果
从数值计算结果发现:
1)50 μs时带隔板装药射流头部速度为7 943.1 m/s,射流长度为294.5 mm;不带隔板装药射流头部速度为6 788.2 m/s,射流长度 253.5 mm,文献[10]中试验结果为7 010 m/s,两者误差为3.3%;
2)SCJ聚能装药中内置隔板后,虽然装药量减少111.3 g,隔板体积占整体的10.7%,但是隔板的存在优化了爆轰波形,最终使得射流速度提高14.5%,射流长度提高13.9%,从而提高了射流的侵彻威力。
在装药种类、长径比和药型罩材料不变的情况下,影响药型罩成型质量因素主要有隔板直径与装药直径的比值Z、隔板厚度L、药型罩锥角α、壁厚δ和隔板距起爆位置距离等参数,文中研究的带隔板装药主要针对小长径比的聚能装药(比如末敏弹等),该结构中各个部件比较紧凑,隔板距起爆位置的距离通常保证装药可以正常起爆以及爆轰波可以正常传播即可。因此通过改变Z、L、α和δ使其相互配合。根据正交优化设计方法[11],将隔板直径与装药直径的比值Z、隔板厚度L、药型罩锥角α和壁厚δ作为本次优化设计的4个因素,各因素水平取值如表1所示。
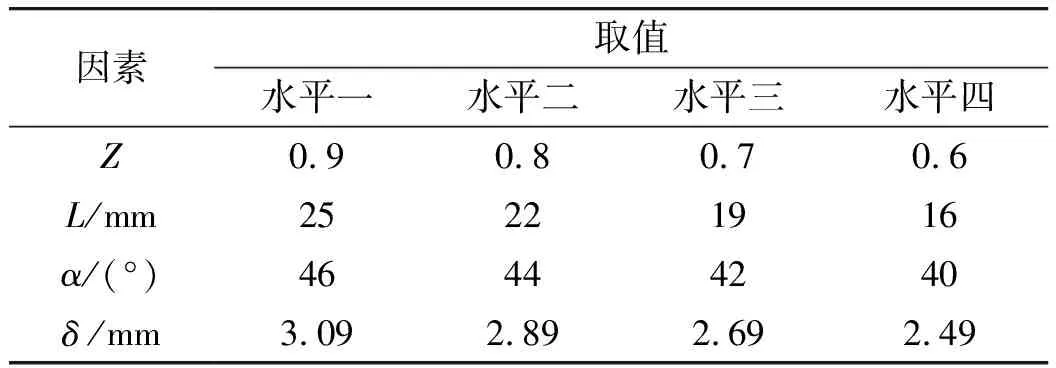
表1 正交优化设计各因素水平取值表
通过数值仿真计算得到高速射流的头部速度和长度,将其作为本次优化设计的两个评定指标。用L16(45)正交表对4个因素所对应的16个水平进行合理安排,得到表2中的16个数值模拟计算方案。
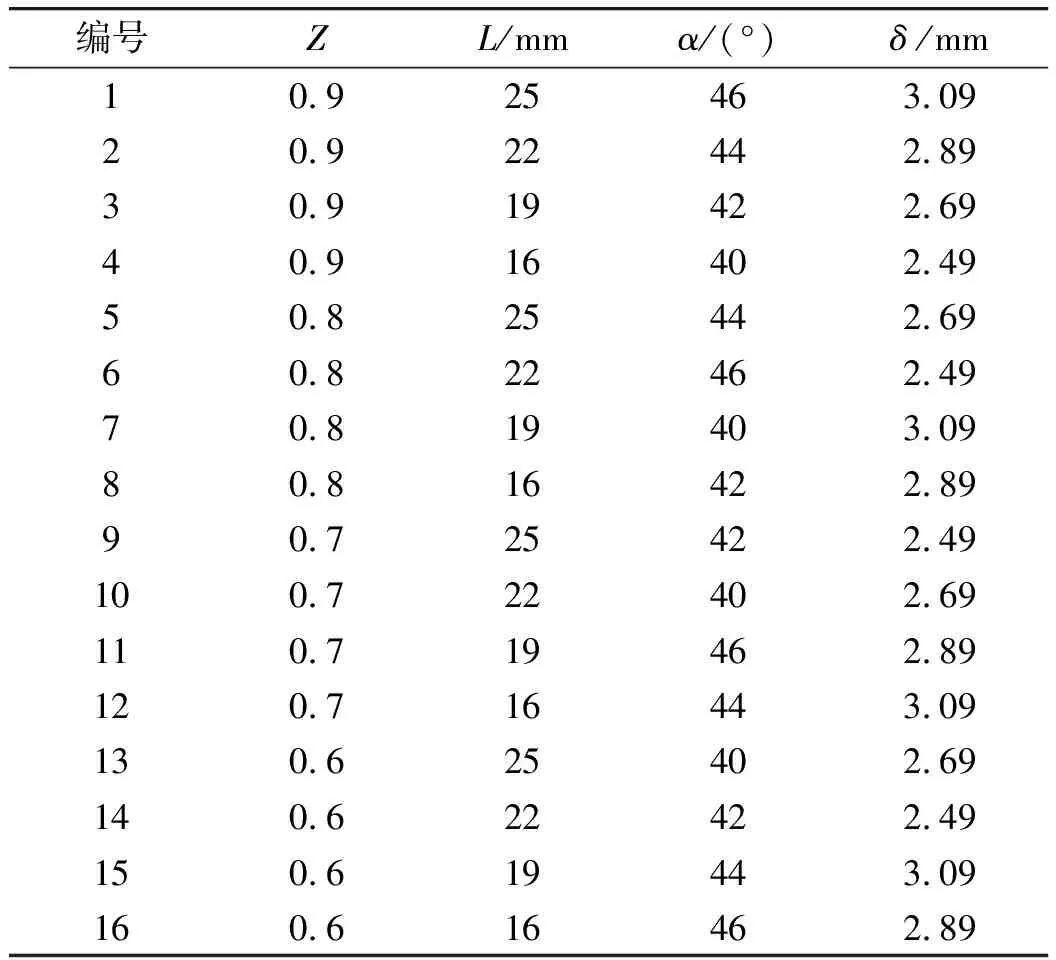
表2 正交优化设计仿真计算方案
按照表2所示的SCJ装药仿真计算方案,分别建立对应的有限元仿真计算模型,依次计算得到聚能射流头部速度、长度和比动能等模拟结果,如表3所示。
通过计算得出:射流头部速度随着Z减小而减小,随着α和δ减小而增大;射流长度随δ减小而增大;比动能随着Z减小而减小,随δ减小而增大。
根据极差分析法知:Z对头部速度v和比动能E都是第一重要目标,Z取0.9时v和E都存在极大值;L对v和E存在极大值时取19 mm;α和δ对v都是第一重要目标影响较大,分别取42°和2.69 mm。所以,最终优化的方案为编号3,此时射流头部速度为9 112.5 m/s,射流长度为310.5 mm。图3为编号3在不同时刻所形成SCJ的成形外形,反映了SCJ的成形过程。

表3 50 μs时高速射流头部速度、长度和比动能
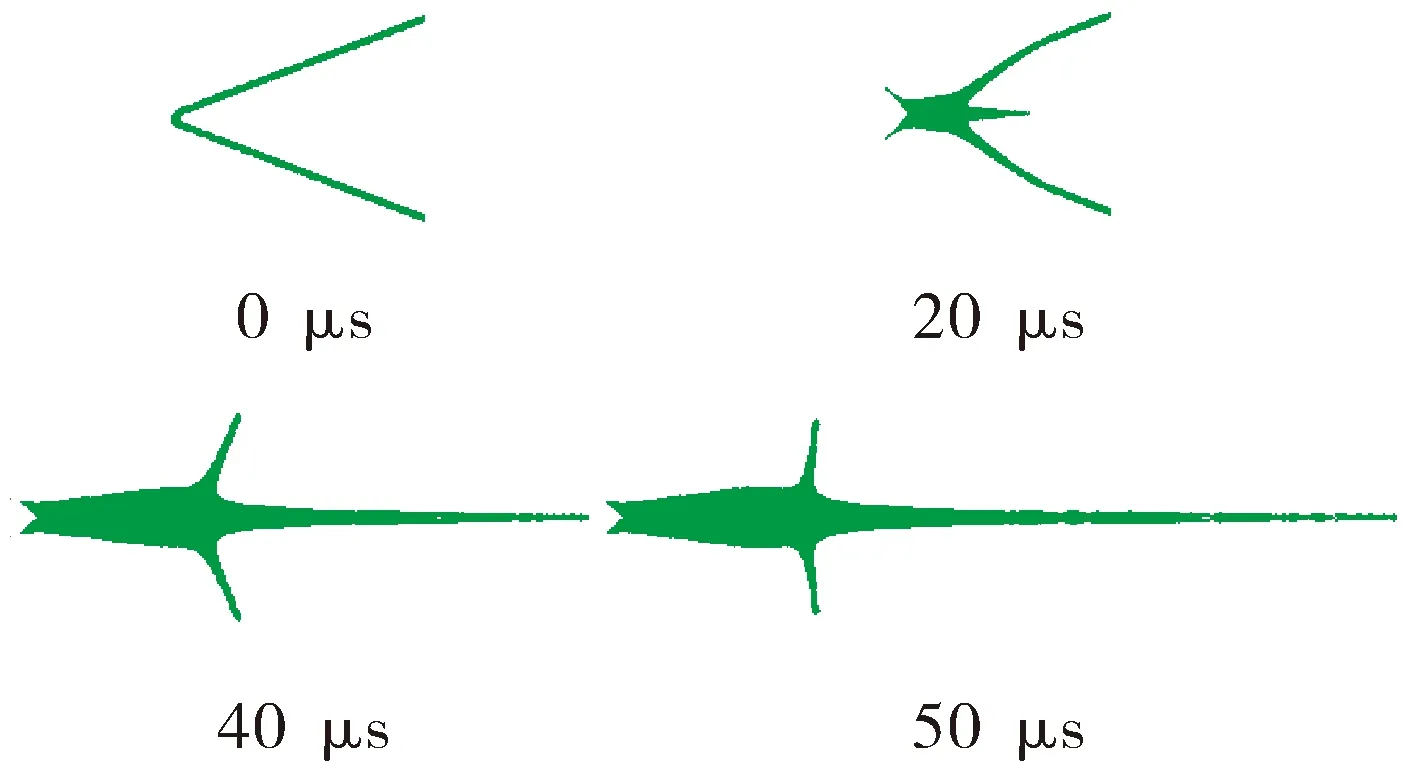
图3 SCJ成形过程数值模拟结果
3.2 隔板结构对杆式射流(JPC)数值仿真计算
JPC装药中隔板结构以倒锥形为主,其结构参数来自于文献[12]的参数。采用中心起爆和8701炸药,装药直径为110 mm,长度为125 mm。采用壁厚和高度不变的偏心亚半球形药型罩,选用紫铜材料,曲率半径为90 mm,偏心距为39 mm,壁厚2.2 mm。
为了探讨隔板结构对杆式射流的速度和长度的影响,开展了有无隔板结构压垮药型罩的数值模拟,杆式射流装药结构及射流成形结果如图4所示。与无隔板装药相比,带隔板装药结构尺寸相同,隔板直径为100 mm,其圆柱段厚度和锥角分别为4.4 mm和110°,选用酚醛树脂材料。
从数值计算结果发现:
1)带隔板装药射流头部速度为8 693.6 m/s,60 μs时射流长度为341 mm;不带隔板装药射流头部速度为7 324.3 m/s,60 μs时射流长度为286.5 mm,计算结果与文献[12]中结果吻合,从而验证了数值模型的正确性。
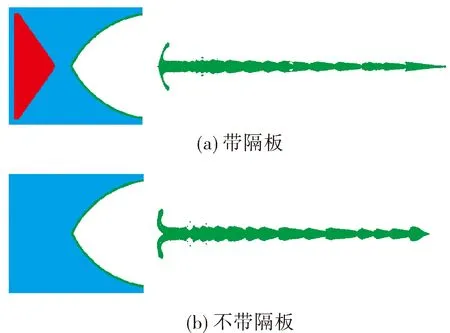
图4 有无隔板K装药结构及射流成形结果
2)JPC聚能装药中内置隔板后,虽然装药量减少214.2 g,隔板体积占据整体的18.7%,但是隔板的存在优化了爆轰波形,在装药中产生超压爆轰,最终使得射流速度提高18.6%,从而可大大提高侵彻威力。
在装药种类、长径比和药型罩材料不变的情况下,影响射流质量的主要因素是Z、偏心亚半球型药型罩的圆心距轴线距离s、药型罩曲率半径r和壁厚δ等参数。根据正交优化设计方法,将Z、s、r和δ作为本次优化设计的4个因素,各因素水平取值如表4所示。
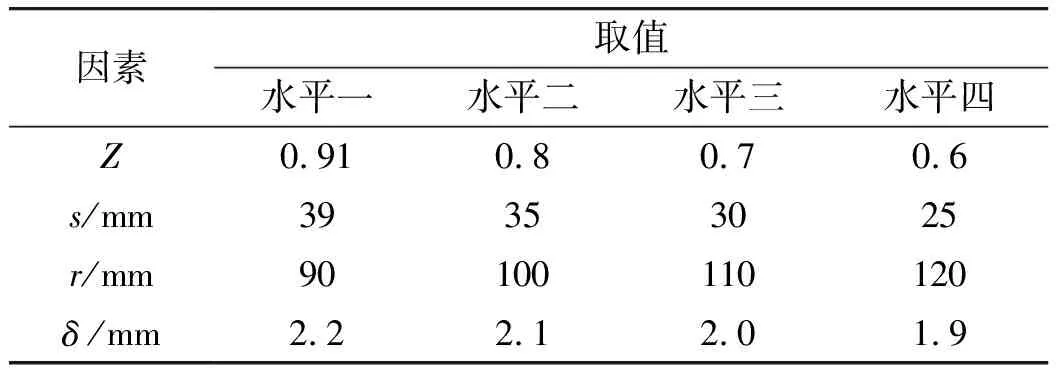
表4 正交优化设计各因素水平取值表
通过数值仿真计算得到杆式射流的头部速度、长度和比动能,将其作为本次优化设计的3个评定指标。用L16(45)正交表对4个因素所对应的16个水平进行合理安排,得到表5中的16个数值模拟计算方案。
按照表5所示的K装药仿真计算方案,分别建立对应的有限元仿真计算模型,依次计算得到杆式射流头部速度、长度和比动能等模拟结果,如表6所示。
通过计算得出:JPC装药头部速度和长度均随Z、s减小而减小,随r增大而减小,随δ减小而增大;比动能随s减小而增大,其他因素在水平二和水平三存在极大值。
根据极差分析法知:Z为头部速度和长度的第一重要指标,所以Z取为0.91;s和r为头部速度和长度的第二重要指标,所以s和r分别取39 mm和90 mm;δ对比动能影响最大应该取2.0 mm,但对于头部速度和长度来讲应该取1.9 mm。
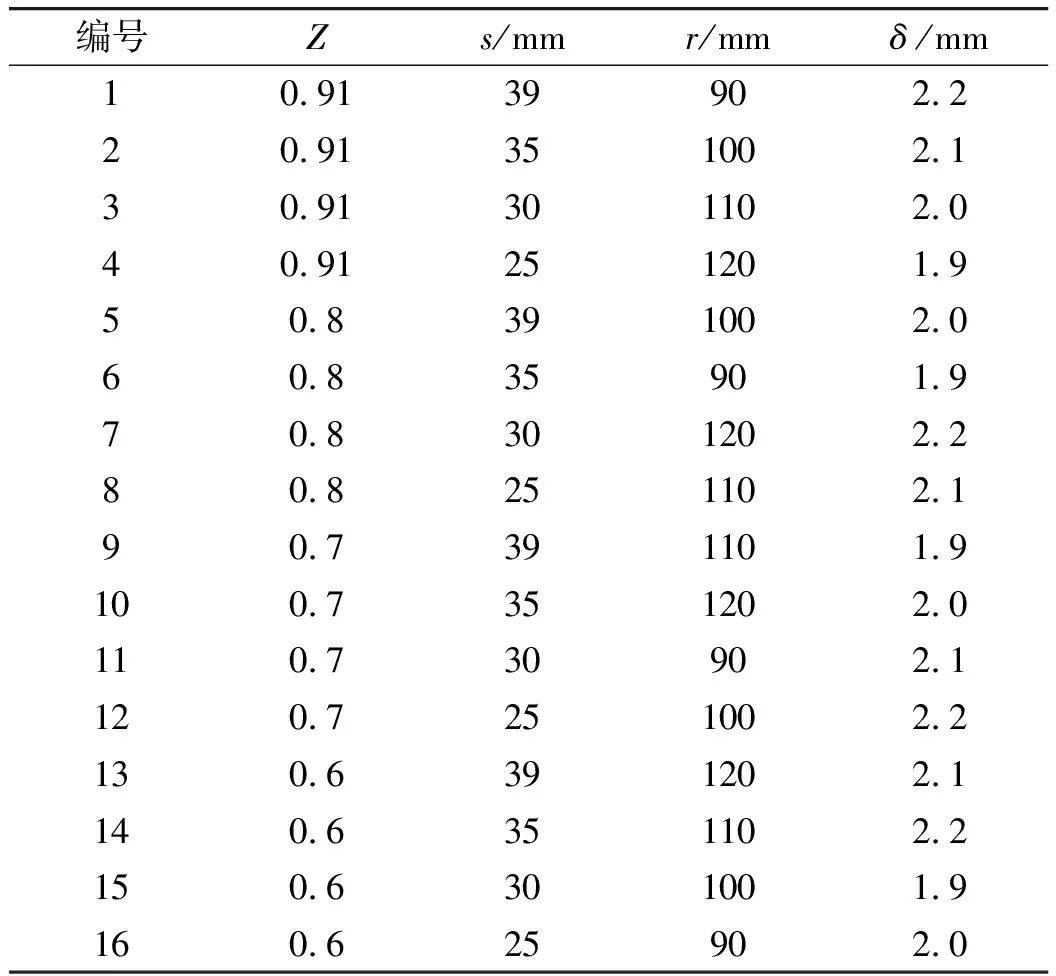
表5 正交优化设计仿真计算方案
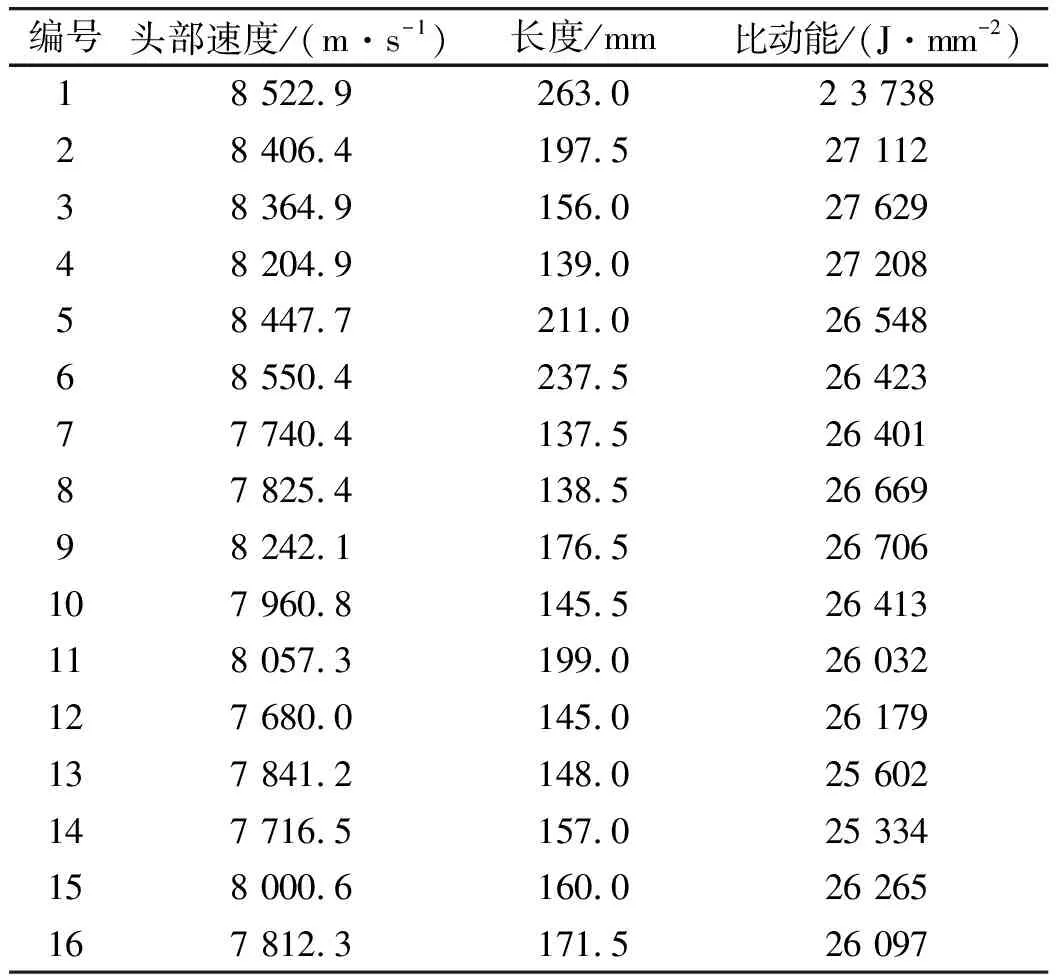
表6 50 μs时杆式射流头部速度、长度和比动能
因此,δ应该在1.9 mm和2.0 mm中取舍,而方案Z=0.91,s=39 mm,r=90 mm并不在表4所给的方案中,需要重新建立数值模型编号为17和18,计算结果如表7所示。
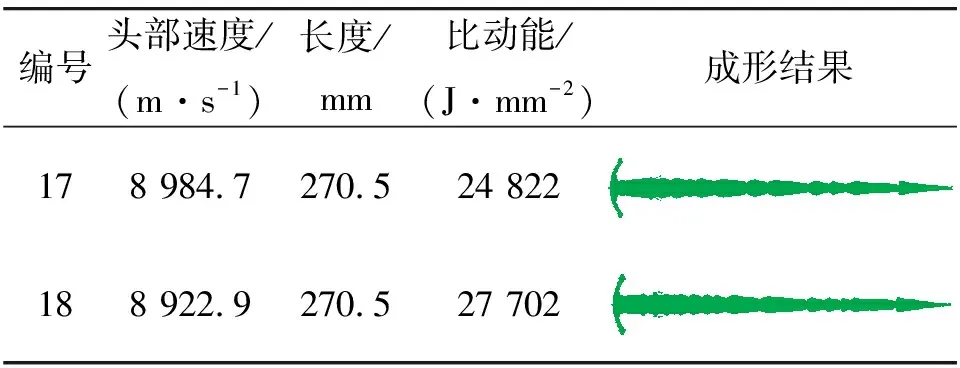
表7 优化方案仿真计算结果
通过优化方案计算结果得出,方案18的各项计算指标均优于表6中的16个方案,其头部速度略低于方案17,但是比动能却高出11.6%,因此,该结构战斗部的优化方案为:Z=0.91,s=39 mm,r=90 mm,δ=2.0 mm。图5为优化后方案在不同时刻所形成JPC的成形外形,反映了SCJ的成形过程。

图5 SCJ成形过程数值模拟结果
3.3 隔板结构对爆炸成型弹丸(EFP)数值仿真计算
带隔板EFP装药,其结构参数来自于文献[13]的参数。采用中心起爆和8701炸药,装药直径为110 mm,长度为88 mm。采用弧锥结合型药型罩,选用紫铜材料,其外半径为75 mm,壁厚7.5 mm,罩口径104 mm。
为了探讨隔板结构对EFP的速度和长度的影响,开展了有无隔板结构压垮药型罩的数值模拟,装药结构及EFP成形结果如图6所示。与无隔板装药相比,带隔板装药结构尺寸相同,隔板直径为66 mm,锥角90°,圆柱段长度为3 mm,采用酚醛树脂材料。

图6 有无隔板EFP装药结构及射流成形结果
从数值计算结果发现:
1)带隔板装药EFP速度为1 336.9 m/s,长径比为3.7;不带隔板装药EFP速度为1 229.0 m/s,长径比为1.4,计算结果与文献[13]中结果吻合,从而验证了数值模型的正确性。
2)EFP装药中内置隔板后,虽然装药量减少了82.0 g,隔板体积占据整个体积的6.7%,但是隔板的存在优化了爆轰波波形,在装药中产生超压爆轰,最终使得EFP的速度提高了8.8%,其长径比提高164.3%,从而大大提高了飞行稳定性。
在装药种类、长径比和药型罩材料不变的情况下,影响EFP质量的主要因素是Z、隔板圆柱段厚度L、弧锥型药型罩曲率半径r和δ等参数。根据正交优化设计方法,将Z、L、r、δ作为本次优化设计的4个因素,各因素水平取值如表8所示。
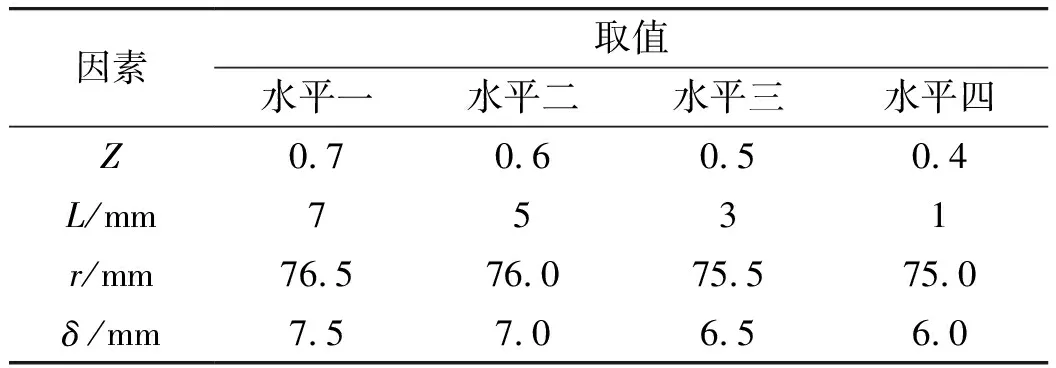
表8 正交优化设计各因素水平取值表
通过数值仿真计算得到EFP速度和长度,将其作为本次优化设计的两个评定指标。用L16(45)正交表对4个因素所对应的16个水平进行合理安排,得到表9中的16个数值模拟计算方案。
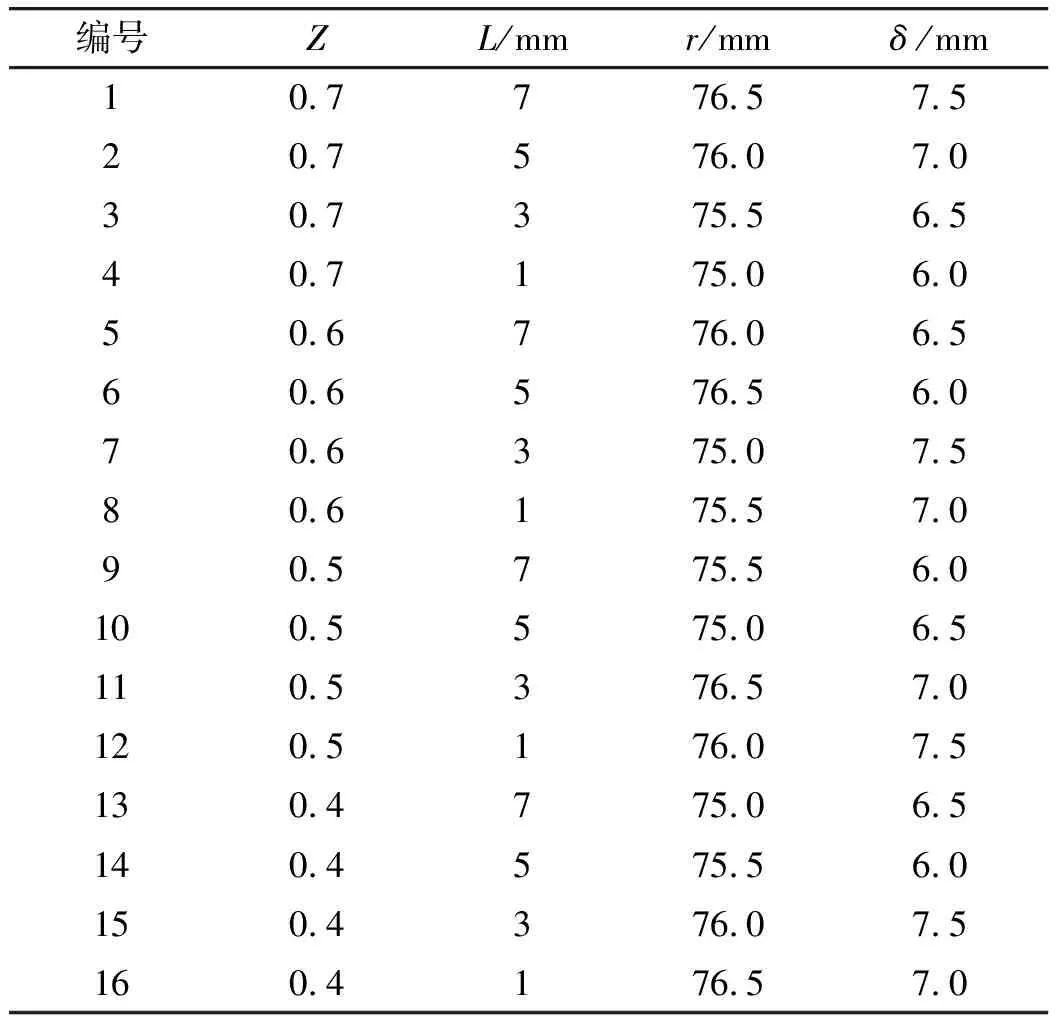
表9 正交优化设计仿真计算方案
按照表9所示的EFP装药仿真计算方案,分别建立对应的有限元仿真计算模型,依次计算得到EFP头部速度、长度和比动能等模拟结果,如表10所示。
通过计算得出:EFP的长径比、头部速度和长度均随Z减小而减小,随δ减小而增大;其他因素在变化中存在极值。
根据极差分析法知:Z和δ为头部速度和长度的第一重要指标,所以Z和δ分别取为0.7和6.0 mm;L和r为头部速度和长度的第二重要指标,且存在极值,故取1 mm和75.0 mm。计算结果如表10中的方案4所示,但EFP在成形和飞行过程中由于速度过高而发生断裂,所以最终优化方案为编号10,Z=0.5,δ=6.5 mm,L=1 mm,r=75.0 mm。图7为优化后方案在不同时刻所形成EFP的成形外形,反映了EFP的成形过程。
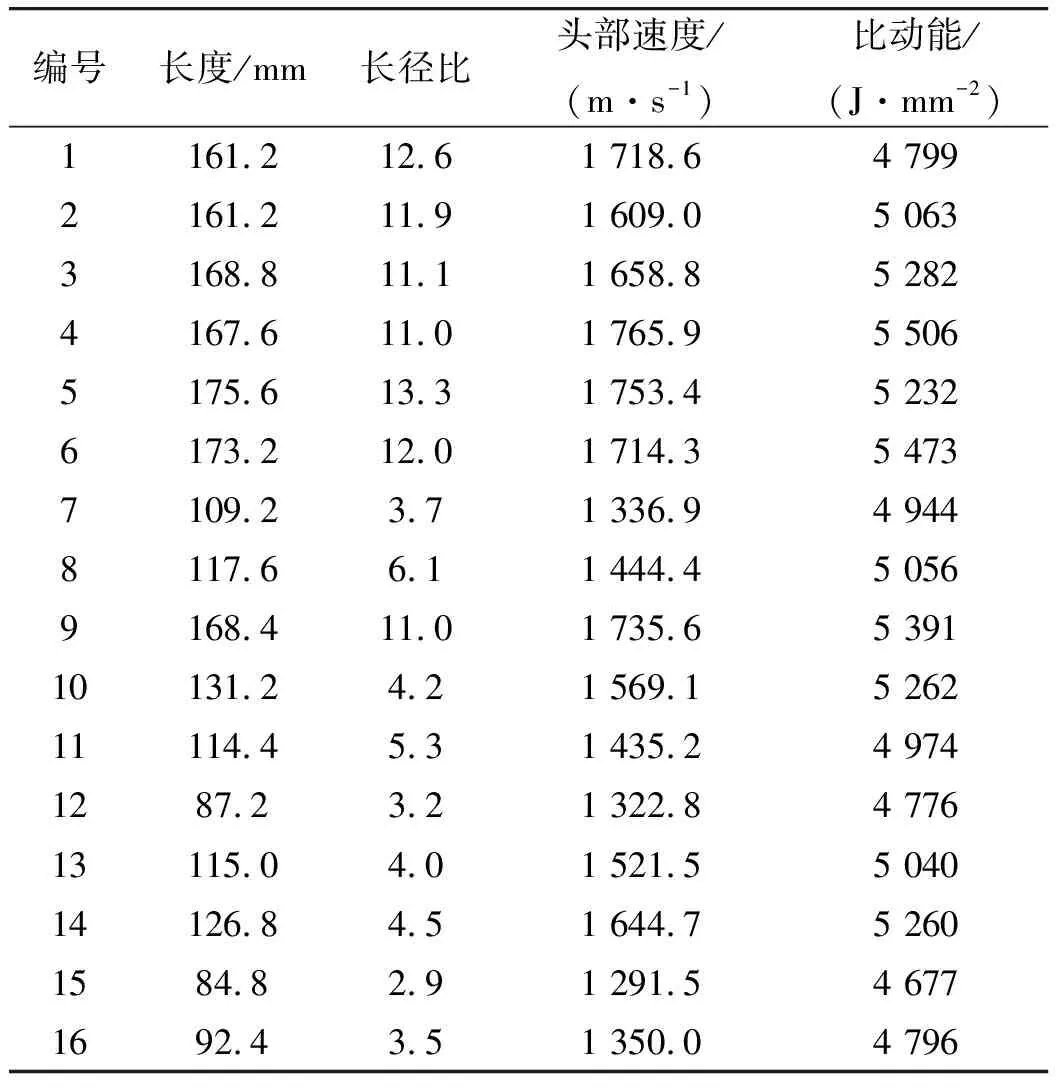
表10 带隔板EFP速度、长度、比动能和长径比
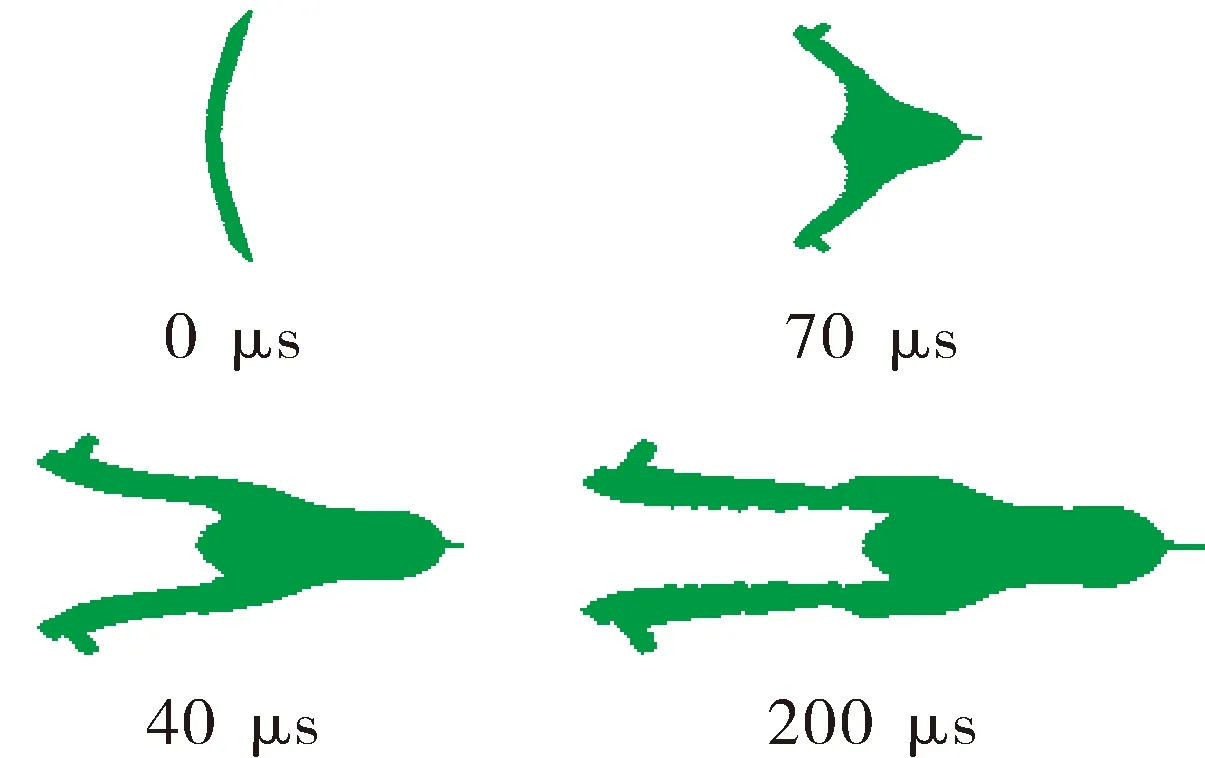
图7 EFP成形过程数值模拟结果
4 结论
对带隔板装药爆轰波驱动药型罩开展数值仿真模拟计算得出,在装药种类、长径比和药型罩材料不变的情况下,通过匹配隔板和药型罩结构提高药型罩成型质量。主要结论如下:
1)装药结构中内置隔板可改变爆轰波传播路径,爆轰波在轴线处相互作用产生超压爆轰,可明显提高炸药对药型罩的驱动能力;
2)通过隔板与药型罩结构之间的正交优化得到两者最佳匹配关系,优化后SCJ装药的头部速度提高25.1%、长度提高11%,优化后JPC装药的头部速度提高18.6%,优化后EFP装药的头部速度提高8.8%,长径比提高164.3%。
