杀爆战斗部打击预警机引战配合效果分析*
2019-12-28赵宏伟陈云俊
赵宏伟,陈云俊
(1 96901部队, 北京 100000; 2 湖北航天飞行器研究所, 武汉 430040)
0 引言
预警机是一种集指挥、控制、通信和情报于一体,用于搜索和监控空中、地面或海上目标,并可指挥引导己方飞机执行作战任务的飞机[1-3]。它能起到活动雷达站和空中指挥中心的作用,在现代战争中具有极为重要的作用。针对这一高价值目标,各国多采用防空导弹进行攻击,如俄罗斯的S-400系列、美国的爱国者系列等。
其中,战斗部主要采用杀爆战斗部,例如大飞散角杀爆战斗部、定向破片式杀爆战斗部、连续杆式杀爆战斗部等。对预警机而言,杀爆战斗部的毁伤模式为“破片杀伤为主,爆破毁伤为辅”[4-6]。实际攻击过程中,预警机飞行轨迹距导弹发射点较远且结构复杂,弹目交会过程中脱靶量较大,引战配合的优化程度将直接决定战斗部对目标的毁伤效果。文中通过建立高精度的数学模型,对弹道末端弹目交汇过程中的引战配合现象进行了研究,系统分析了脱靶量、交会速度对破片命中率的影响情况,给出了不同弹道条件下的最佳起爆延时量,为引战配合的优化提供了重要思路。
1 战斗部方案介绍
文中以一种杀爆战斗部为例对引战匹配效果进行分析。其中破片采用Φ6的钨珠,数量不少于7 000枚,破片的静态飞散角为30°,方位角为89°。
根据格尼公式,可以得到飞散破片的静爆初速约1 600 m/s,距爆心20 m处的破片动能约为1 800 J。
2 引战匹配模型建立
2.1 弹目交会模型简述
图1为弹道末端弹目交会示意简图,图中O点为战斗部中心,C为目标中心,R表示弹目之间距离。假定弹体沿着OX方向以一定相对速度朝着目标运行,引信在O点开机,经过一段时间飞行到A点引信探测到目标,其后经过一段时间的延时到B点起爆战斗部,破片命中目标造成毁伤。
上述的弹目交会过程为简要示意,在实际的弹目交会过程中,弹体和目标以一定的姿态飞行,同时脱靶量和脱靶方位也存在变化,因此在模型的构建过程中引入大地坐标系、弹体坐标系、目标坐标系、相对速度坐标系,不同坐标系之间存在一定的转换关系,并以此建立了引信探测模型、弹目交会模型、战斗部破片飞散模型[7-8]。

图1 弹目交会示意图
2.2 引信探测模型
研究中采用无线电周向引信,探测体制为脉冲多普勒,波束倾角Ωf、波束宽度φ及最大作用距离已知。此外,基于引信实际应用中的高灵敏度,可认为在交会过程中引信波束一旦触碰到目标模型即开始启动。因此,在弹体坐标系中,引信可以用两个顶点位于坐标原点的圆锥面近似,如图2所示。图中引信探测波束由一系列离散的直线表示,直线数量越多则引信模型精度越高。
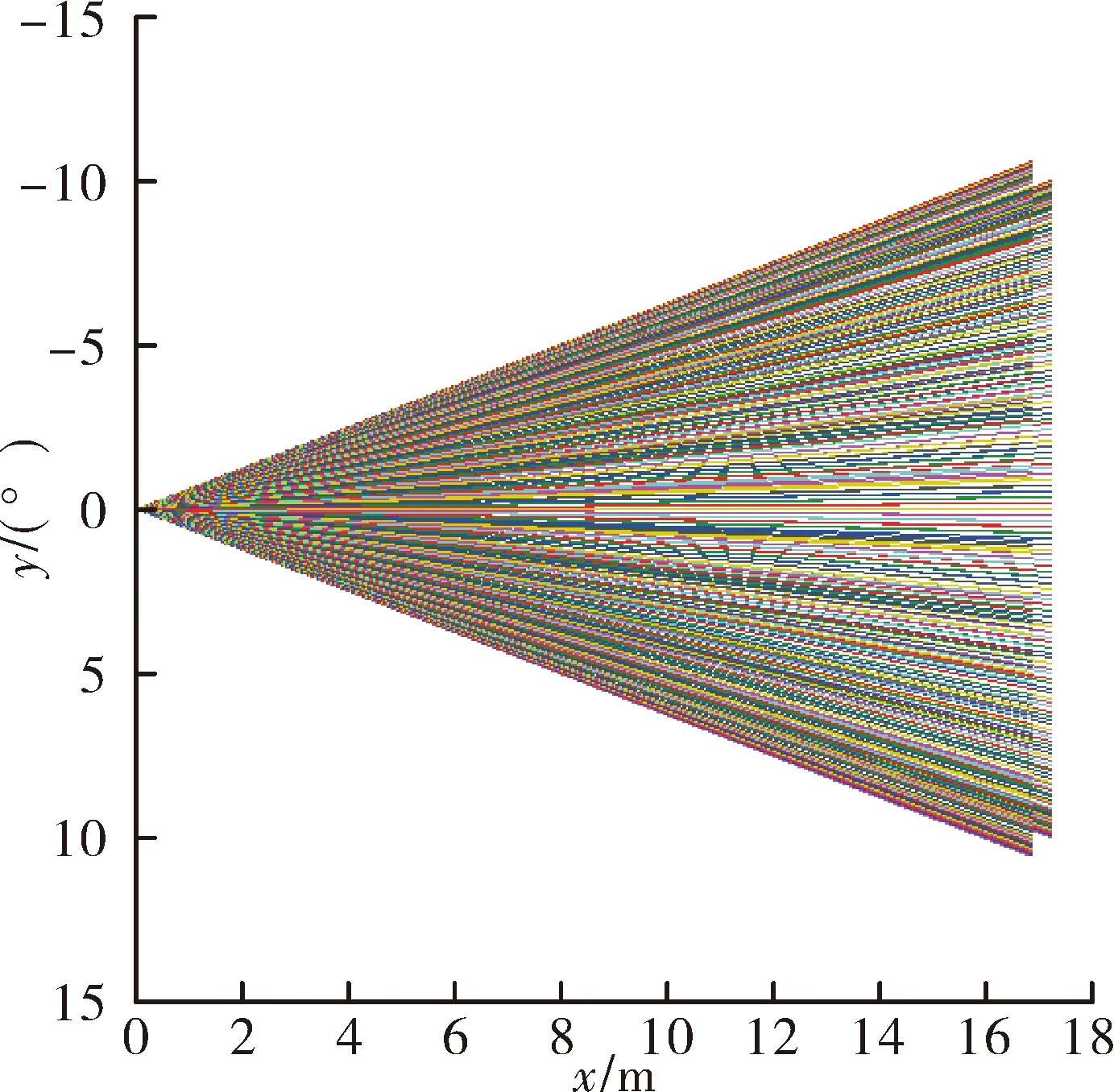
图2 引信探测模型示意图
2.3 破片飞散模型
对破片而言,当静态飞散中心方向角φ0和静态飞散角Δφ已知,则可利用一系列以起爆点为起点的射线来描述破片的飞散模型,且在Δφ宽度内破片数量均匀分布。对静态飞散的破片而言,弹体坐标系中的速度矢量υ0可用飞散方向角φ和飞散方位角ω来描述:
(1)
式中φ和ω的定义如图3所示。
建模过程中破片的真实飞行速度需与弹头的相对飞行速度进行合成,如式(2)所示把所有速度矢量统一转换到大地坐标系中进行运算。
υ=υ0+υr
(2)

图3 破片飞散方向角φ和方位角ω示意图
2.4 破片命中目标模型
建模过程中,首先根据预警机的结构特征利用三维建模软件建立预警机的数学模型如图4所示。
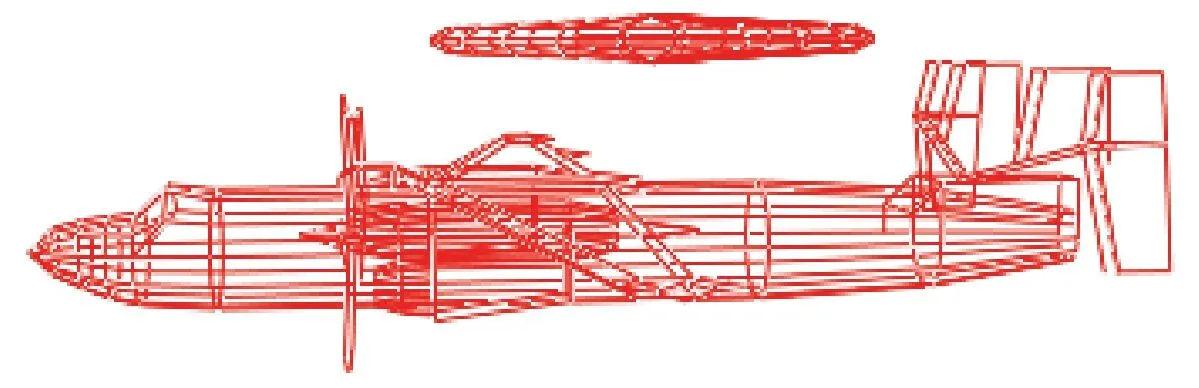
图4 目标预警机数学模型
图中,预警机模型被离散成为一系列面元。计算过程中破片命中目标实质上为判断描述破片的射线与目标面元是否相交,相应的物理过程顺利转化为数学问题的求解。
3 典型弹道下的仿真结果
基于上文描述的战斗部,对典型弹道条件下引战配合情况进行了仿真计算。交会过程中,相对速度倾角θ小于40°,不考虑偏航角,相对速度范围为800~1 800 m/s,脱靶量设定在20 m以内,脱靶方位随机。
图5给出的是脱靶量为7 m,相对速度为800 m/s,速度倾角为10°和40°时,脱靶方位分别为0°、45°、90°、135°、180°下的延时量-命中率曲线。由图可知,由于脱靶量和相对速度较小,对应最大命中率的延时量较大,即当延时量为(16±1) ms时,最大命中率约为20%;此外在当前弹道条件下,脱靶方位为90°时命中效果最佳,即在目标正下方起爆时命中率最大。
对应的,图6给出了脱靶量为7 m,相对速度为1 800 m/s,交会倾角为10°和40°时,不同脱靶方位下的延时量-命中率曲线。对比图5中的计算结果可见,两种情况下得到的曲线趋势大体相同,但由于相对速度的增大,引战配合难度加大,最佳延时量为(5±1)ms,对应最大平均命中率约为15%。
图7给出的是脱靶量为14 m,相对速度为800 m/s,速度倾角为10°和40°时,不同脱靶方位下的延时量-命中率曲线。与图5类似,当延时量为(16±1) ms时取得最大破片命中率,但由于脱靶量增加了一倍,命中率降幅超过了50%,对应最大命中率平均值约为9%,表明脱靶量的大小对破片命中率有显著影响。

图5 ρ=7 m,υr=800 m/s不同脱靶方位下破片命中率情况

图6 ρ=7 m,υr=1 800 m/s不同脱靶方位下破片命中率情况
对应的,图8给出的是脱靶量为14 m,相对速度为1 800 m/s,速度倾角为10°和40°时,不同脱靶方位下的延时量-命中率曲线。根据计算结果可知,延时量为(2±0.5) ms时,对应最大命中率平均值约为7%,对比图7的结果进一步验证了交会速度的增加增大了引战配合的难度。

图7 ρ=14 m,υr=800 m/s不同脱靶方位下破片命中率情况
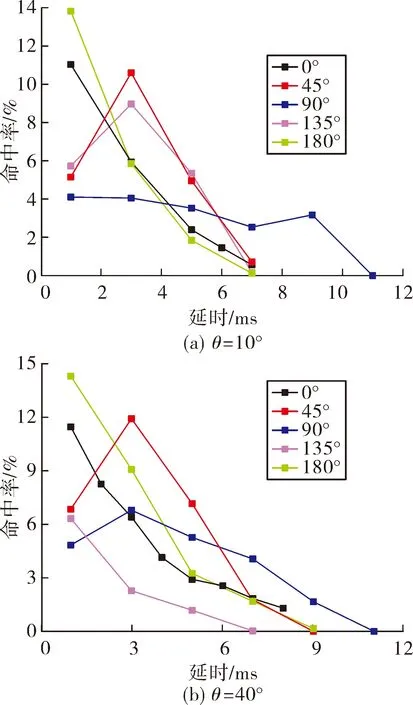
图8 ρ=14 m,υr=1 800 m/s不同脱靶方位下破片命中率情况
图9和图10分别给出的是脱靶量为20 m,相对速度为800 m/s及1 800 m/s,速度倾角为10°和40°时,不同脱靶方位下的延时量-命中率曲线。根据计算结果可知,相对速度小,延时量为(15±1) ms时取得最大命中率平均值约为5%;相对速度大时,最好的引战配合方式为探测即起爆,延时量在1 ms左右,对应最大命中率平均值约为3%。
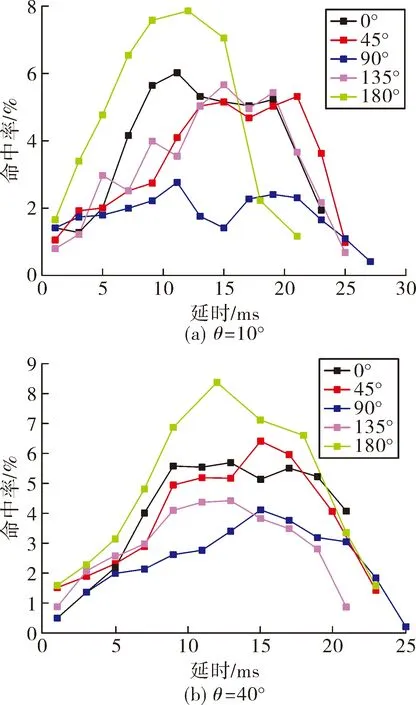
图9 ρ=20 m,υr=800 m/s不同脱靶方位下破片命中率情况
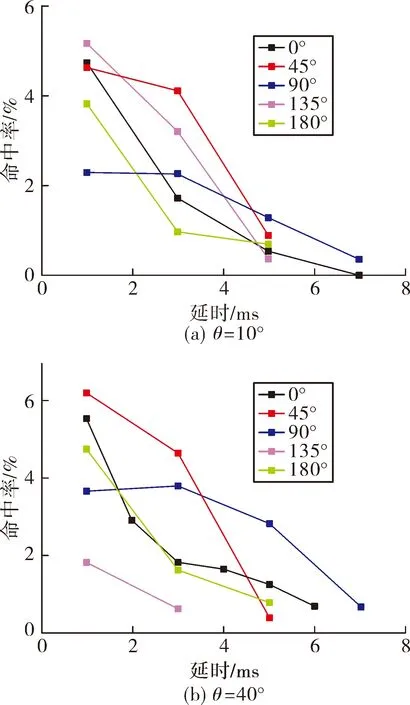
图10 ρ=20 m,υr=1 800 m/s不同脱靶方位下破片命中率情况
表1总结了以上典型弹道情况下的仿真结果,通过不同情况下计算结果的对比可更进一步反映脱靶量和相对速度对破片命中率的影响情况。

表1 仿真结果总结(不同弹道条件下的最佳延时量及命中情况)
4 结论
文中基于实际的军事需求,构建了杀爆战斗部打击预警机的引战配合数学模型。以某型杀爆战斗部为例,对典型弹道条件下的引战配合情况进行了仿真,通过对仿真结果的系统分析可以得到如下结论,为引战配合的优化提供了重要依据。
1)相对速度较小时,最佳延时量较大,对应引战配合难度较小;
2)对当前交会情况而言,相对速度较小时,即使脱靶量增加,最佳延时量并没有明显的变化;
3)随着脱靶量和相对速度的增加,最佳延时量及破片命中率都会显著降低,即引战配合难度显著增加;
4)脱靶量及相对速度的大小都会影响破片命中率,但脱靶量的影响更为明显。
