学习数学历史，领悟殊途同归

南京市第一中学高三（12）班 江天翼

在数学学习中，老师经常鼓励我们一题多解.这是很好的方法，有助于我们增强想象力，将知识融会贯通.其实，在数学发展过程中，有无数的数学家、科学家、思想家，在不同国度、不同年代、不同学科研究着相同的问题，尝试着更高层次、更大问题的一题多解.本文结合数学史，分析勾股定理、庞加莱猜想的殊道同归，抛砖引玉.

一、勾股定理

我国古代称直角三角形的两条边为“勾和股”，称斜边为“弦”.在直角三角形中，两条直角边的平方和等于斜边的平方，此结论在我国被称为“勾股定理”.早在周朝初年（约公元前1100年），周朝大夫商高就发现了直角三角形的一个特例：“勾三、股四、弦五”，亦称“商高定理”.

在西方，这个定理被称为“毕达哥拉斯定理”，亦称“百牛定理”，是公元前500余年由古希腊数学家毕达哥拉斯发现的.尽管比中国人的发现晚了500～600年，但相传毕达哥拉斯对这一发现十分重视，曾宰牛百头用来祭祀缪斯女神（希腊神话中掌管文艺、科学之神）.

勾股定理是我们最熟悉的平面几何中的一个最著名、最精彩、最有用的定理，是数学大厦的一块基石，被天文学家开普勒誉为几何学的一大宝藏.勾股定理至今仍活跃在人们心里，具有强大的生命力，各种证法接连涌现、层出不穷.据说，现在世界上已有500种证明方法，鲁密斯（Loomis）搜集整理的《毕达哥拉斯定理》一书第二版中，就搜集了370种不同的证法.本文列举几种简单而优美的证法.

1.赵爽证法

三国时，赵爽在《勾股方圆图注》中，采用了证明几何问题的割补原理.

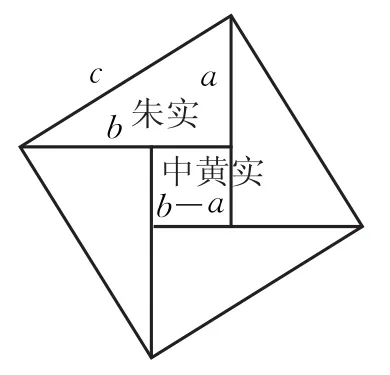
图1

2.伽菲尔德证法

如图1，以a，b，c表示勾、股、弦，以a，b为直角边的每个直角三角形叫做“朱实”，即图中有4个“朱实”，中间的一个以b-a为边长的小正方形叫做“中黄实”，以弦c为边长的大正方形叫做“弦实”，此图为“弦图”，由图可知：c2=（b-a）2+4ab=a2+b2.

詹姆斯·艾伯拉姆·伽菲尔德（1831～1881），美国政治家、数学家、教育家，第20任美国总统.1876年，他还是一名众议员时，就发现了勾股定理的一种巧妙证法（用两种办法计算同一梯形的面积），并发表在《新英格兰教育杂志》上.

图2

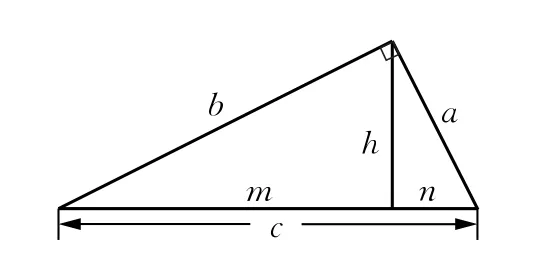
图3

3.现代相似三角形证法

作三边长分别为a，b，c的直角三角形，斜边c上的高为h，得到两对相似三角形（如图3），从而可列出两组比例式：

二、庞加莱猜想

法国著名数学家亨利·庞加莱（1854～1912）的研究涉及分析学、数论、代数学、几何学、拓扑学等诸多领域，发表论文500多篇，出版科学著作30部，被公认为19世纪末到20世纪初世界数学界的领袖人物.他在1904年发表的一组论文中，提出其猜想：“单连通的三维闭流形可简单地理解为一种曲面同胚于三维球面.”后又被推广为：“任何与n维球面同伦的n维闭流形必定同胚于n维球面.”这就是著名的“庞加莱猜想”.

“庞加莱猜想”是拓扑和几何的主流，是国际数学界长期关注的一个重大难题，被列为七大“数学世纪难题”之一（设在波士顿的克莱数学研究所于2000年5月24日将它列为“千禧年七大难题”之一，并悬赏100万美元奖励这一猜想的证明者）.“庞加莱猜想”的证明有助于科学家加深对流形性质的认识，进一步认识我们所生存的空间，并对物理学和工程学的发展产生重要影响.美国《科学》杂志评出2006年十大科学进展，证明“庞加莱猜想”位列榜首.

庞加莱本人曾力图证明这一猜想，但终究未能成功.1960年之前，所有证明（或否证）“庞加莱猜想”的尝试都未能如愿.1960年，美国传奇数学家史蒂芬·斯梅尔证明庞加莱猜想对五维和五维以上的情形是成立的.20年后，另一位美国数学家米歇尔·弗里德曼证明了四维流形拓扑的庞加莱猜想.两人因此分别获得1966年和1986年的菲尔兹奖.这样，庞加莱猜想只剩下三维情形没有解决，而该猜想当初恰恰是针对三维球面而提出的.

解决“庞加莱猜想”有几种不同的途径，刚开始是拓扑学方法，即所谓切割方法，但这个方法到20世纪70年代就很难进步了.1978年，美国数学家威廉·瑟斯顿引进几何结构方法来做切割，讨论了三维流形上的叶状结构，并对一般流形上叶状结构的存在、性质及其分类得出了普遍的结果，基本完成了三维闭流形的拓扑分类，获得1982年的菲尔兹奖.

1982年，美国数学家理查德·汉密尔顿发表了一篇文章，提出一种名为“瑞奇流”的数学工具来构造几何结构，这是用微分方程来做的.但他在用“瑞奇流”进行空间变化时，遇到了“奇异点”.如何处理“奇异点”就成为整个庞加莱猜想中最重要的部分.

被誉为“数学隐士”的俄罗斯数学家格里高里·佩雷尔曼在2002年11月和2003年7月之间，将3份关键论文的手稿粘贴到专门刊登数学和物理预印本论文的网站上，并用电邮通知了几位数学家，声称自己证明了几何化猜想.而“庞加莱猜想”正是几何化猜想的一个特例.

2006年，朱熹平（中山大学教授）、曹怀东（中国旅美数学家、美国里海大学讲座教授、清华大学兼职教授，师从丘成桐）在美国数学集团创办的《亚洲数学期刊》（2006年6月号）上发表论文，标题为“庞加莱猜想和几何化猜想的完全证明：汉密尔顿佩雷尔曼关于RICCI流理论的应用”，共328页.文章一步一步、清清楚楚、完完整整地写出了整个证明过程.

简而言之，可以认为：在攻克“庞加莱猜想”战役中，汉密尔顿和丘成桐（著名华裔数学家，获得菲尔兹奖、沃尔夫奖、克莱福特奖这三个世界顶级大奖）一起发展了一套纲领——用“瑞奇流”来解决这个问题，为破解猜想奠定了基础.基于3篇网站上发表的论文手稿，佩雷尔曼称他完成了这个纲领.而一个完整的解释由曹怀东、朱熹平完成.汉密尔顿在2006年8月西班牙马德里举行的第25届国际数学家大会上，明确地表达了这个观点，清楚地提到了丘成桐、曹怀东、朱熹平的贡献.由于菲尔兹奖只授予40岁以下做出杰出贡献的青年数学家，只有佩雷尔曼因此获得当年的菲尔兹奖.但不知何故，他拒绝领奖.

学习数学史，了解数学家的探究精神，领悟数学问题和思维方法，具有十分重要和鲜明的现实意义.在很多数学概念、定理的发现、证明中，都活跃着中国前辈的身影，这让我油然而生崇高的敬意和强烈的民族自豪感，暗暗发奋，要更加热爱数学，钻研数学，提高数学水平.