挖掘考题功能,学会思考类比
——以一道圆锥曲线高考题的探究为例
2019-12-24江苏省扬州市新华中学王梅蓉龚海滨
江苏省扬州市新华中学 王梅蓉 龚海滨
在一次拓展课课后作业中,同学们仔细研究了下面这个问题:
(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.
对于第(2)问同学们形成了五种各具特色的解题思路.
一、思路分析
思路1 利用斜率之和为0
当l与x轴重合时,∠OMA=∠OMB=0°;当l与x轴垂直时,因为OM为AB的垂直平分线,所以∠OMA=∠OMB;当l与x轴不重合也不垂直时,如图1,根据图形的特征,把要证的∠OMA=∠OMB转化为直线斜率之间的关系kMA+kMB=0.设直线l的方程为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2),将直线与椭圆方程联立,利用根与系数的关系以及斜率公式依靠代数运算即可证得结论.
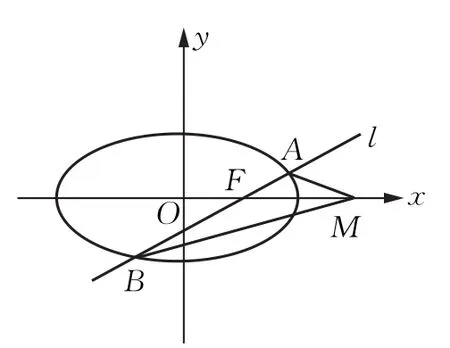
图1
思路2 利用角平分线性质
当l与x轴不重合也不垂直时,如图2,设点O到直线MA,MB的距离分别是d1,d2,直线l的方程为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2),则MA:y1x+ (2-x1)y-2y1=0,MB:y2x+(2-x2)y-2y2=0.根据角平分线的性质,将要证的∠OMA=∠OMB转化为证明d1=d2,即证再将直线与椭圆方程联立,利用根与系数的关系即可证得结论.
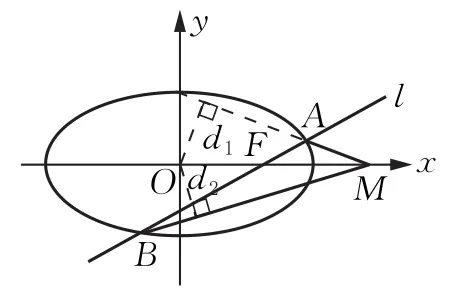
图2
思路3 利用三角函数值相等
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2),要证∠OMA=∠OMB,只要证tan∠OMA=tan∠OMB,如图3,过A点作AA′⊥x轴,垂足为A′,过B点作BB′⊥x轴,垂足为B′,又只要证,即证以下同思路2.
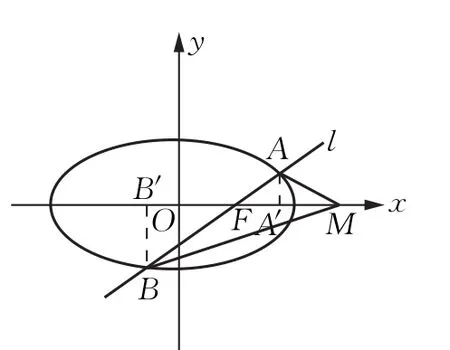
图3
思路4 利用三角形相似
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2),如图3,过A点作AA′⊥x轴,垂足为A′,过B点作BB′⊥x轴,垂足为B′,要证 ∠OMA=∠OMB,只要证△MA′A∽△MB′B,又只要证即只要证以下同思路2.
思路5 利用向量数量积
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1)(k≠0),A(x1,y1),B(x2,y2),运用向量的数量积公式将∠OMA和∠OMB看成是对应的两向量的夹角,则∠OMA=即证两边平方,化简得以下同思路2.
二、探究解疑
学起于思,思起于疑.常有疑点,常有问题,才能常有思考,常有创新.一道数学题解出答案并不是解题思维活动的结束,而是更深入探究的开始.
问:点M是个特殊点吗?它的背后是否有一些我们没有发现的东西呢?
哦,原来点M恰好是椭圆右准线与x轴的交点.于是我们有如下结论:
结论1设AB是过椭圆的焦点F(c,0)(c>0)的弦,M为椭圆的右准线l与x轴的交点,则MF平分∠AMB.
问:再回顾以上几种思路,是否可以将其优化呢?
不难发现,我们可以将思路4优化一下,借助于椭圆第二定义来证明三角形相似.

图4
证明:如图4,过A,B两点分别作右准线l的垂线,垂足分别是A1,B1,则从而又因为由 ∠AA1M=∠BB1M=90°,知△AA1M∽△BB1M,从而 ∠A1AM=∠B1BM,所以∠AMF=∠BMF,则MF平分∠AMB.
上述这种解法灵活运用了圆锥曲线的第二定义,取得了简捷、合理的解题效果.学好数学最重要的法宝就是对数学概念的精通.
“特殊化和类比是获得发现的伟大源泉”,类比可以引领我们提出新问题、发现新结论、开创新方法.
问:椭圆、双曲线、抛物线有很多相似的性质,双曲线和抛物线的焦点弦是否也有同样的性质呢?
关于双曲线、抛物线的焦点弦与相应准线同学们可以猜想并证明如下性质:
结论2设AB是过双曲线的焦点F(c,0)(c>0)的弦(点A,B都在双曲线的右支上),M为双曲线的右准线与x轴的交点,则MF平分∠AMB.
结论3设AB是过抛物线y2=2px(p>0)的焦点)的弦,M为抛物线的准线与x轴的交点,则MF平分∠AMB.
问:能将上述结论中的圆锥曲线的焦点一般化吗?例如,在结论1中,若将F(c,0)变为椭圆内定点P(m,0),则点M的坐标又是什么?MP平分∠AMB仍然成立吗?
结论4如图5,设P(m,0)为椭0)内一定点,过点P作直线交椭圆于A,B两点,若直线与x轴交于点M,则MP平分∠AMB.
将结论4类比到双曲线、抛物线可以得到同样的结论:
结论5已知双曲线过点P(m,0)(m>a)作直线交双曲线于A,B两点(点A,B都在双曲线的右支上),若直线x=与x轴交于点M,则MP平分∠AMB.
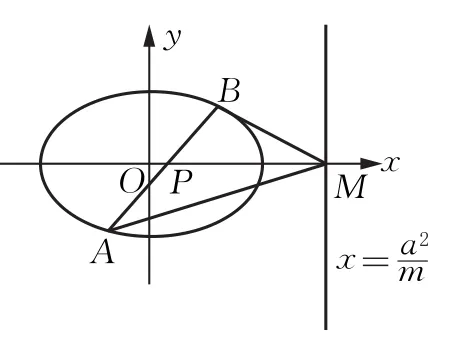
图5
结论6过抛物线y2=2px(p>0)的对称轴上的任意一点P(m,0)(m>0)的作直线与抛物线交于A,B两点,点M是点P关于原点的对称点,则MP平分∠AMB.
通过探究,我们感受到了圆锥曲线的和谐美和统一美,学会了类比、猜想、证明等科学研究的方法.与圆锥曲线有关的问题一般都是非常有趣的,值得研究的,如能深入其中,我们一定会被它形式的美妙、内容的和谐所吸引,流连忘返,美不胜收!
高考题有很强的代表性,我们在研究高考题时要深挖问题的本质,重视和加强对问题的拓展、引申和变式研究,最大可能地让其功能得到充分的发挥,这才是学习之本.过程往往比结果更为重要,探索问题的意义已经远远超过了问题解决的本身.学习数学就应该这样勇于探索,敢于创新!
