单调性与导数
2019-12-24苏州市吴江盛泽中学吴敏强
苏州市吴江盛泽中学 吴敏强
我们在学习导数的时候,老师一定告诉过你:
对于函数y=f(x),如果在某区间上f′(x)>0,那么f(x)在该区间上单调递增;如果在某区间上f′(x)<0,那么f(x)在该区间上单调递减.
对于这个结论,你也一定背得滚瓜烂熟了,那么我想问一句,这是为什么呢?
在学习导数之前,对于函数单调性的判断我们手边的方法有:
1.画出函数图象,直观判断;
2.利用函数单调性的定义.
我们先来回顾一下函数单调性的定义:
设函数y=f(x)的定义域为A,区间I⊆A.如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数.如果对于区间I内的任意两个值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间I上是单调减函数.
在之前的文章中我们提到过,这个定义是可以修正改进的,如下:
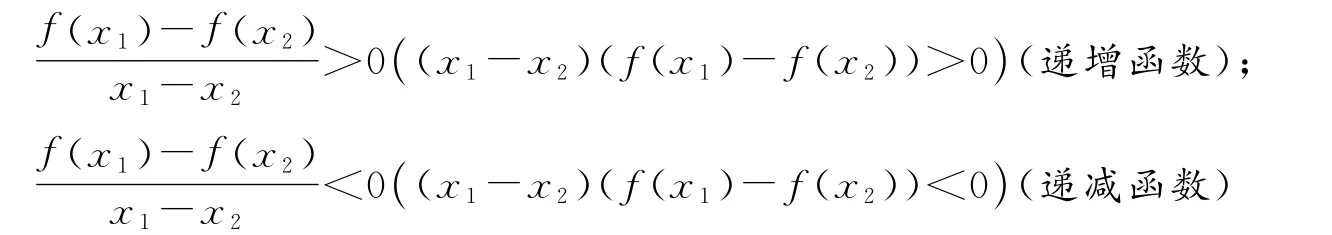
然后,我们再来看看导数是怎么回事?导数的定义如下:
设函数y=f(x)在区间(a,b)上有定义,x0∈(a,b),当Δx→0时,比值则称f(x)在x=x0处可导,并称A为f(x)在x=x0处的导数.
对于一个结论,想要认识清楚,原命题研究完后,研究其逆命题、否命题,对辨析概念效果甚佳.
原命题:对于函数y=f(x),如果在某区间上f′(x)>0,那么f(x)在该区间上单调递增;
逆命题:对于函数y=f(x),如果在某区间上单调递增,那么f(x)在该区间上f′(x)>0.
逆命题是真命题还是假命题呢?答案:假命题.
反例:f(x)=x3,在定义域R上单调递增,其导函数f′(x)=3x2,很显然当x∈R,f′(x)≥0恒成立,可见上述逆命题是不正确的.那教科书的描述错了吗?没有,教科书没错,只是f′(x)>0并不是y=f(x)单调递增的充要条件,而仅仅是充分条件而已.
那好,现在我们对它进行修正,我想你一定会这样做,把等号加上去.
命题1:对于函数y=f(x),如果在某区间上f′(x)≥0,那么f(x)在该区间上单调递增.
上述命题比之前的原命题更加完备,但还是存在缺陷,下面我用具体函数来说明,如图1:


图1
大家可以很容易通过计算得到上述分段函数分别在区间[0,2),(2,4)和(4,+∞)上是可导的,且在各区间上导函数f′(x)≥0恒成立,而图象中间一段是水平线,所以整个图象并不是单调递增的.这说明什么?
问题还是出在f′(x)=0的那些点上,上述函数f′(x)=0的点是连续的,形成了区间,于是就有了一段不增的函数段,换言之,f′(x)=0不能形成区间!
命题2:对于函数y=f(x),如果在某区间上f′(x)≥0,且f′(x)=0的点不能形成区间,那么f(x)在该区间上单调递增.这个命题是充要的!
这个等号是很重要的.
最后看一个习题,来体会下等号的重要性.
解答:因为函数在R上单调递增,所以f′(x)=x2+2bx+(b+2)≥0在R上恒成立,且f′(x)=0的点不能形成区间,故4b2-4(b+2)≤0,解得-1≤b≤2.
可见这个等号是需要的.
对于概念的理解我们不能知其然不知其所以然,更不能局限于死记硬背,我们要有打破砂锅问到底的精神!数学,让我们无所畏惧!
